Summary:
The number of electric field lines that pass through any closed surface is called the electric flux which is a scalar quantity.
Electric flux solved examples
In the following, a number of solved examples of electric flux are presented. More simple problems including flux of uniform or non-uniform electric fields are also provided.
Example (1): electric flux through a cylinder.
Suppose in a uniform electric field a cylinder is placed such that its axis is parallel to the field.
To compute the flux passing through the cylinder we must divide it into three parts top, bottom, and curve then the contribution of these parts to the total flux must be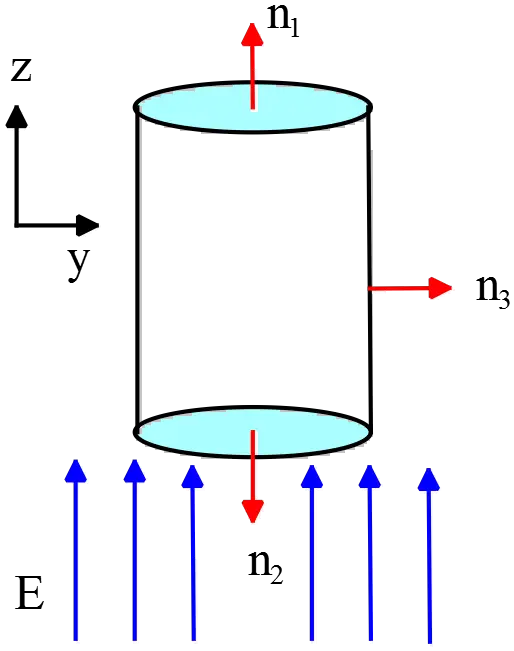 summed.
summed.
On the top and bottom sides, the unit normal vectors are $\hat k$, $-\hat k$, respectively. Let $\vec E$ be toward the $z$ axis i.e. $\vec E=E\hat k$.
Scalar products of top and bottom sides by electric field make the total flux since the normal vectors and $\vec E$ are parallel ($\theta =0$) and antiparallel ($\theta=180^\circ$), respectively.
The curve side has a normal vector in the radial direction which makes a right angle($θ=90^\circ$) with $\vec E$ so its contribution to the flux is zero. \begin{align*} \oint{\vec E\cdot \hat n dA}&=\int{\vec E_1\cdot\hat k dA_1}+\int{\vec E_2 \cdot \left(-\hat k\right) dA_2}\\ &+\int{\vec E_3 \cdot \hat r dA_3}\\&=E_1 A_1 -E_2A_2\end{align*}
$E_1$, $E_2$ and $E_3$ are the amount of electric fields passing through the surfaces. Since the electric field is uniform one can factor it out of the integral.
$A_3$ is the area of the curved side which is $2\pi Rl$. The electric field lines don’t pass through the curved sides and only penetrate top and bottom which in this case their amounts are the same $E_1=E_2$.
Therefore, the total flux through the cylinder is simply \[\Phi_E=0\]
This result is expected since the whole electric field entering the bottom side exiting the top surface.
Example (2):
A hemisphere of radius $R$ is placed in a uniform electric field such that its central axis  is parallel to the field. Find the electric flux through it?
is parallel to the field. Find the electric flux through it?
Solution:
Let the electric field be in the $z$ direction i.e. $\vec E=E_0 \hat k$. The normal vector to the hemisphere is in the radial direction so $\hat n=\hat r$. Further, the area element of a spherical surface of a constant radius in the spherical coordinate is 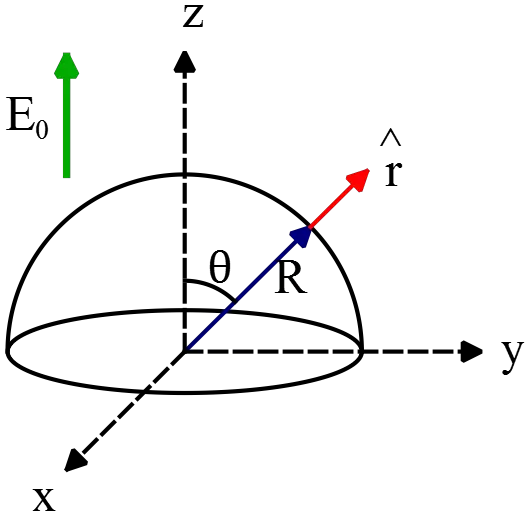 $dA=R^{2}\,\sin\theta\, d\theta d\phi$.
$dA=R^{2}\,\sin\theta\, d\theta d\phi$.
Therefore,
\begin{align*}\Phi_E&=\int{\vec E\cdot \hat n\,dA}\\&=\int{\left(E_0\hat k\right)\cdot \hat r R^{2}\,\sin \theta d\theta d\phi}\end{align*}
No we must find the scalar product of $\hat r\cdot \hat k$. In spherical coordinates we have the following relation for the unit vector in the radial direction:
\[\hat r=\sin \theta \cos \phi \, \hat i+\sin \theta \sin \phi \, \hat j+\cos \theta \, \hat k\]
Where $\hat i,\hat j,\hat k$ are the usual unit vectors in the Cartesian coordinates. Thus
\[\hat r\cdot \hat k=\cos \theta\]
Where we have used the fact that $\hat i\cdot \hat k=\hat j\cdot \hat k=0$ and $\hat k\cdot \hat k=1$. Putting everything into the electric flux relation, one can obtain
\begin{align*}\Phi_E&=E_0R^{2}\int_0^2\pi{d\phi}\int_0^{\pi/2}{\underbrace{\cos \theta \sin \theta}_{\frac 12 \sin 2\theta}d\theta}\\&=E_0R^{2}\left(2\pi\right)\frac 12\left(-\frac 12\,\cos 2\theta\right)_0^{\pi/2}\\&=\pi E_0R^{2}\end{align*}
Example (3):
consider a planar disc of radius $12\,{\mathrm cm}$ that makes some angle $30^\circ$ with the uniform electric field $\vec E=450\,\hat i\,\mathrm {(N/C)}$. What is the amount of electric flux passing through it?
Solution:
Let the electric field be in the x-direction and normal to the plane be in some direction $\hat n$ which must be decomposed into the $x$ and $y$ directions, as shown in the 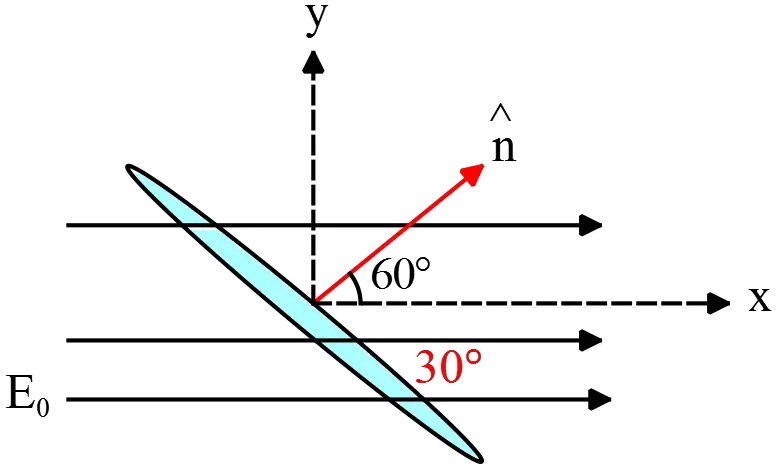 figure. Using the definition of electric flux, we have
figure. Using the definition of electric flux, we have
\begin{align*} \Phi_E&=\int{\vec E\cdot \hat n dA}\\&=\int{E_0\hat i \cdot\left(\cos 60^\circ\,\hat i+\sin 60^\circ \,\hat j\right)dA}\\&=E_0\,\cos 60^\circ\int{dA}\end{align*}
Where the integral over $dA$ is the area of the disk which is $\pi R^{2}$. Therefore
\begin{align*}\Phi_E&=E_0\left(\frac 12\right)\left(\pi R^{2}\right)\\&=(450)\left(\frac 12 \right)\pi (0.12)^{2}\\&=10.17 \quad \rm {\frac {N\cdot m^{2}}{C}}\end{align*}
Another method for finding electric flux due to systems with high symmetry is to use Gauss's law. You can also learn this elegant method with some simple problems.
Author: Ali Nemati

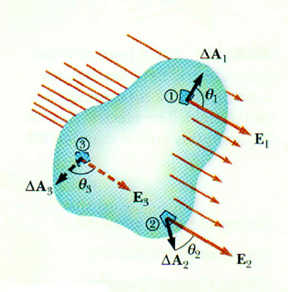 field lines in the closed surface by the area of the surface.
field lines in the closed surface by the area of the surface.