Unit Vector: Practice Problems, Formula

A unit vector is defined with the following properties
   (i) Its magnitude is always 1.
   (ii) It has no unit.
   (iii) It is parallel to a coordinate axis or any arbitrary vector. In the other words, this vector describes a direction.

Therefore, any vector with these properties is called a unit vector.

If each component of an arbitrary vector is divided by its magnitude, the resulting vector is a unit vector.

Recall that a vector in physics is defined as a quantity that has both a magnitude and a direction.

Therefore, the unit vector in the direction of vector $\vec{w}$ with magnitude of $|\vec{w}|$ is found by the following formula \[\hat{w}=\frac{\vec{w}}{|\vec{w}|}\] To distinguish a unit vector from an ordinary vector, a caret or $\hat{}$ is used.

If you are getting ready for AP physics exam 1, check this:
Vectors in the AP physics exam.

In the following, a number of simple problems about unit vectors are answered that are useful for high school students.

Unit Vector Practice Problems

Problem (1): Find the unit vector in the direction $\vec{w}=(5,2)$.

Solution: A unit vector in physics is defined as a dimensionless vector with a magnitude of exactly 1.

To determine a unit vector that points in the direction of a given vector, $\vec{A}$, we use the formula: \[\hat{A}=\frac{\vec{A}}{|\vec{A}|}\] Here, $|\vec A|$ represents the magnitude of the vector $\vec{A}$, which is calculated as: \[|\vec{A}|=\sqrt{A_x^2+A_y^2}\]

To find the unit vector points in the same direction as the given vector, $\vec{W}$, follows these steps: Calculate the magnitude of $\vec{w}$: \[|\vec{w}|=\sqrt{5^2+2^2}=\sqrt{29}\] Divide the vector $\vec{w}$ by its magnitude: \[\hat{w}=\frac{(5,2)}{\sqrt{29}}=\left(\frac{5}{\sqrt{29}},\frac{2}{\sqrt{29}}\right)\] Thus, the unit vector in the direction of $\vec{w}=(5,2)$ is $\left(\frac{5}{\sqrt{29}},\frac{2}{\sqrt{29}}\right)$.

Problem (2): What is the unit vector point in the direction of $\vec{v}=(-4,-8)$?

Solution: The unit vector along any given vector is calculated by dividing the vector by its magnitude.

The magnitude of the given vector can be determined using the formula: \[|\vec{v}|=\sqrt{(-4)^2+(-8)^2}=\sqrt{80}\] Thus, applying the definition of a unit vector, we have: \[\hat{v}=\frac{(-4,-8)}{\sqrt{80}}=\left(\frac{-1}{\sqrt{5}},\frac{-2}{\sqrt{5}}\right)\] In the step, the magnitude was simplified using $\sqrt{80}=\sqrt{16\times 5}=4\sqrt{5}$.

Problem (3): Find the unit vector in the direction of the sum of two vectors $\vec{v}=(2,-4)$ and $\vec{w}=(-3,2)$.

Solution: the sum of two given vectors, denoted as $\vec{c}$, is calculated as follows: \begin{align*} \vec{c}&=\vec{v}+\vec{w}\\&=(2,-4)+(-3,2)\\&=(2+(-3),-4+2)\\&=(-1,-2)\end{align*} Next, the magnitude of this vector is calculated using the formula: \[|\vec{c}|=\sqrt{(-1)^2+(-2)^2}=\sqrt{5}\] Finally, to find the unit vectorin the direction of $\vec{c}$, divide $\vec{c}$ by its magnitude: \[\hat{c}=\frac{(-1,-2)}{\sqrt{5}}=\left(\frac{-1}{\sqrt{5}},\frac{-2}{\sqrt{5}}\right)\]

Problem (4): Find a vector in the direction of unit vector $\hat{v}=\left(1/3,\sqrt{8}/3\right)$ that has a magnitude of 11.

Solution: By definition, a unit vector has a length (magnitude) of 1. To verify this property for the given vector, we calculate its magnitude using the Pythagorean theorem: \[|\hat{v}|=\sqrt{(1/3)^2+(\sqrt{8}/3)^2}=1\] This confirms that $\hat{v}$ is indeed a unit vector. Using the definition of a unit vector, we can construct a vector with any desired magnitude.

If a unit vector is scaled by a constant coefficient $k$, the resulting vector has a magnitude of $k$. Mathematically, this is expressed as: \[\vec{w}=k\hat{v}\]

To find a vector with a magnitude of 11 in the same direction as the given unit vector $\hat{v}$, we scale $\hat{v}$ by 11. Thus, the required vector is: \[\vec{u}=11\hat{v}=\left(\frac{11}{3},\frac{11\sqrt{8}}{3}\right)\]
In the final step, we used the property of scalar multiplication for a vector, defined as: \[k(a,b)=(ka,kb)\]

Problem (5): Find the unit vector in the direction of the resultant vectors $\vec{A}=2\hat{i}-3\hat{j}+4\hat{k}$ and $\vec{B}=-\hat{i}+\hat{j}+2\hat{k}$.

Solution: The given vectors are in three-dimensional space, and their components are provided. The sum of two vectors is known as the resultant vector.

To find the resultant vector, $\vec{C}=\vec{A}+\vec{B}$, we apply the formula for vector addition: \begin{align*}\vec{C}&=\vec{A}+\vec{B}\\&=(2,-3,4)+(-1,1,2)\\&=(2+(-1),-3+1,4+2)\\&=(1,-2,6)\end{align*} Thus, the resultant vector is: $\vec{C}=(1,-2,6)$.

Next, using the definition of a unit vector (vector components divided by its magnitude), we calculate the magnitude of $\vec{C}$.

Finally, dividing each component of $\vec{C}$ by its magnitude, the unit vector in the direction of $\vec{C}$ is: \begin{align*}\hat{c}&=\frac{\vec{C}}{|\vec{C}|}\\\\&=\frac{(1,-2,6)}{\sqrt{1^2+(-2)^2+6^2}}\\\\&=\left(\frac {1}{\sqrt{41}} ,\frac {-2}{\sqrt{41}} ,\frac {6}{\sqrt{41}}\right)\end{align*}

More related:
Practice problems on vectors

Problem (6): In the following figure, (a) write each vector in terms of unit vectors $\hat{i}$ and $\hat{j}$, (b) Use unit vector definition to express the vector $\vec{C}=3\vec{A}-2\vec{B}$.

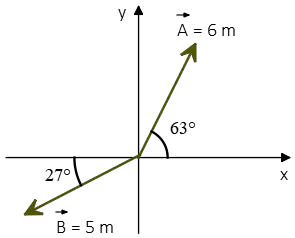
Solution: The unit vectors $\hat{i}$ and $\hat{j}$ represent the directions of the x- and y- axes, respectively, and have a magnitude of 1. The magnitudes and directions (angles) of the given vectors are provided.

(a) First, resolve the given vectors into their components.

For a vector $\vec{A}$ with magnitude $|\vec{A}|$, the components are determined as follows: \begin{gather*} \vec{A}_x=|\vec{A}|\cos\theta \\ \vec{A}_y=|\vec{A}|\sin\theta \end{gather*} We can also write the vector in the usual form by summing its components with their corresponding unit vectors: \[\vec{A}=\vec{A}_x\hat{i}+\vec{A}_y\hat{j}\] Using the above method, the decomposition of the given vectors is as follows: \begin{align*} \vec{A}_x&=6\cos 63^\circ =2.72\,{\rm m}\\ \vec{A}_y&=6\sin 63^\circ=5.34 \\\\ \vec{B}_x&=5\cos 27^\circ=4.45 \\ \vec{B}_y&=5\sin 27^\circ=2.7\end{align*} The components of a vector along the x- and y-axes can be expressed in terms of unit vectors as: \begin{gather*} \vec{A}_x=|\vec{A}|\hat{i}\\\vec{A}_y=|\vec{A}|\hat{j}\end{gather*} Combining everything, the given vectors in terms of unit vectors are: \begin{gather*} \vec{A}=2.72\hat{i}+5.34\hat{j} \\ \vec{B}=4.45\hat{i}+2.7\hat{j}\end{gather*}
(b) Next, we multiply $\vec{A}$ by 2 and subtract $2\vec{B}$ from the result.

According to the rules of scalar multiplication, each component of a vector is multiplied by the scalar. Thus: \[2\vec{A}=2(2.72,5.34)=(5.44,10.68)\] Similarly, \[2\vec{B}=2(4.45,2.7)=(8.9,5.4)\] To subtract two vectors, subtract their respective components: \begin{align*}\vec{C}&=3\vec{A}-2\vec{B}\\&=(5.44,10.68)-(8.9,5.4)\\&=(-3.46,5.28)\end{align*} Using the Pythagorean theorem, the magnitude of this vector is: \[|\vec{C}|=\sqrt{(-3.46)^2+(5.28)^2}=6.31\] Finally, to find the unit vector in the direction of the $\vec{C}$, divide each component of $\vec{C}$ by its magnitude: \begin{align*} \hat{c}&=\frac{\vec{C}}{|\vec{C}|}\\\\&=\frac{(-3.46,5.28)}{6.31}\\\\&=(0.55,0.84)\end{align*} You can verify that the magnitude of this unit vector is indeed 1.

Author: Ali Nemati
Date Published: 6/19/2021