AP Physics 1: Vectors Practice Problems with Answers
Explore a comprehensive guide to practicing vector problems specifically for the AP Physics 1 exam.
This article features sample problems on vector addition and subtraction, dot and cross product, resultant vectors, and more.
Note: These problems are designed solely for practice and do not reflect the style or accuracy of the actual AP Physics 1 exam.
Additionally, if you’re looking for a straightforward, visual, and easy-to-read equation sheet for the AP Physics 1 exam, be sure to download it.
Solved Vector Problems:
Problem (1): Which of the following quantities are vectors in physics?
a. Electromotive force (emf).
b. Electric current.
c. Fluid pressure.
d. gravitational field.
Solution: Those quantities that have both a direction and a magnitude are defined as vector quantities in physics, such as displacement, velocity, acceleration, force, and so on.
Both electromotive force (emf) and electric current are not vectors since a number is sufficient to describe them completely.
Pressure at the depth of a fluid is not a vector, either. The gravitational field at any point has both a direction and a magnitude.
Thus, the correct answer is d.
Problem (2): Which of the following quantities are scalars in physics?
(a) Momentum
(b) Displacement
(c) Area
(d) Average velocity
Solution: Many quantities in physics do not have any direction associated with them. Just a number or a unit fully describes them. Such quantities are called scalar quantities. Examples of scalar quantities are mass, time, area, temperature, emf, electric current, etc.
Thus, the correct answer is c.
Be sure to read this article: Definition of a Vector in Physics. There you will find more problems on vectors.
Problem (3): The components of a vector are given as $A_x=5.3$ and $A_y=2.9$. What is the magnitude of this vector?
(a) 3 (b) 6 (c) 4 (d) 5
Solution: the magnitude of a vector in component form is found using the Pythagorean formula as below: \[A=\sqrt{A_x^2+A_y^2}\] Substituting the numerical values of the components into the above equation, we have \[A=\sqrt{(5.3)^2+(2.9)^2}=\boxed{6}\] The correct answer is b.
Problem (4): We are given the components of a displacement vector as $d_x=23.5$ and $d_y=34.3$. What angle does this vector make with the positive $x$-axis?
a. $34.4^\circ$ b. $67^\circ$
c. $55.6^\circ$ d. $17.3^\circ$
Solution: Once the components of a vector are known, we can find its direction from the $x$-axis by the following formula: \[\alpha=\tan^{-1}\left(\frac{d_y}{d_x}\right)\]
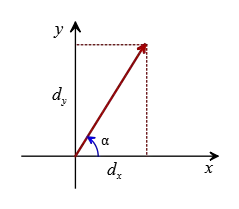
Substituting the components gives us \[\alpha=\tan^{-1}\left(\frac{34.3}{23.5}\right)=55.6^\circ\] Since all components are in the first quadrant, so this is the correct angle.
Thus, the correct answer is c.
More Problems about vector components are discussed in the article below.
Vector practice problems
Problem (5): The components of a velocity vector at a moment are given as $v_x=-9.8\,{\rm m/s}$ and $v_y=6.4\,{\rm m/s}$. The direction, from the $+x$-axis, and magnitude of this velocity vector (in $\rm m/s$) are closest to
a. $11.7\, , 147^\circ$ b. $12.7\, , 139^\circ$
c. $11.7\, , -33.15^\circ$ d. $11.7\, , 211.15^\circ$
Solution: Its magnitude is simply obtained using the Pythagorean theorem \begin{align*}v&=\sqrt{v_x^2+v_y^2}\\\\&=\sqrt{(9.8)^2+(6.4)^2}\\\\&=\boxed{11.7\,{\rm m/s}}\end{align*} The subtle point is finding its direction. Note that the components of this vector lie in the second quadrant. Using the equation in the previous problem, it gives us \begin{align*} \alpha&=\tan^{-1}\left(\frac{v_y}{v_x}\right) \\\\ &=\tan^{-1}\left(\frac{6.4}{-9.8}\right)\\\\&=-33.15^\circ\end{align*}
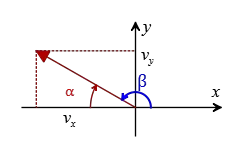
Pay attention to these notes when using this equation for finding the direction of a vector relative to the $x$-axis through the smallest angle (as shown in the figure by $\alpha$):
Note (1): In the one and fourth quadrants, the formula gives the correct angle.
Note (2): In the second and third quadrants, add $180^\circ$ to the angle obtained from the formula.
In this case, therefore, the correct angle is \[\beta=180^\circ+(-33.15^\circ)=\boxed{146.85^\circ}\] which can be rounded to $147^\circ$, Hence, the correct answer is a.
Problem (6): Two equal magnitude forces, forming an angle of $60^\circ$ with each other, act on a body. What is the ratio of their subtraction to their resultant?
a. $\frac{\sqrt{3}}{3}$ b. $\sqrt{3}$
c. $1$ d. $\frac{\sqrt{2}}{2}$
Solution: This question aims to explore the concepts of vector subtraction and addition (the same resultant). Assume two vectors (say, force) $\vec{A}$ and $\vec{B}$. The magnitude of their subtraction,$\vec{C}=\vec{A}-\vec{B}$, is defined to be as \[ C=\sqrt{A^2+B^2-2AB\cos\theta}\] where $A$ and $B$ are the magnitudes of each vector separately, and $\theta$ is the angle between them.
In this case, we're told that there are two equal magnitude forces, i.e., $F_1=F_2=F$. Substituting the values into the above, we will have \begin{align*} C&=\sqrt{F_1^2+F_2^2-2F_1 F_2 \cos\theta} \\\\ &=\sqrt{2F^2-2F^2 \cos 60^\circ}\\\\&=\boxed{F}\end{align*} where we used $\cos 60^\circ=\frac 12$. On the other side, the resultant vector is another name for the addition of vectors, $\vec{R}=\vec{A}+\vec{B}$. The magnitude of the resultant of two arbitrary vectors making an angle of $\theta$ is given by \[R=\sqrt{A^2+B^2+2AB\cos\theta}\] Thus, in this case, we have \begin{align*} R&=\sqrt{F_1^2+F_2^2+2F_1 F_2\cos\theta}\\\\ &=\sqrt{2F^2+2F^2 \cos 60^\circ}\\\\&=F\sqrt{3}\end{align*} Now their ratio is as \[\frac{C}{R}=\frac{F}{F\sqrt{3}}=\frac{1}{\sqrt{3}}\] By rationalizing the denominator, the ratio is obtained as $\frac{\sqrt{3}}{3}$.
Thus, the correct answer is a.
More related problems on forces in the AP Physics 1 Exam:
AP Physics 1 forces practice problems with MCQs.
Problem (7): The magnitudes of two displacement vectors are $d$ and $2d$, and the magnitude of the total displacement is also $d\sqrt{3}$. What is the angle between these two displacement vectors?
a. $\frac{3\pi}{4}$ b. $\frac{\pi}{4}$
c. $\frac{2\pi}{3}$ d. $\frac{\pi}{2}$
Solution: Displacement is a vector quantity in physics. Here, we have two displacement vectors of magnitudes $d$ and $2d$. The total displacement vector is the same as the resultant (or net) vector that is obtained by adding the vectors. Recall that the magnitude of a resultant vector of two vectors $\vec{A}$ and $\vec{B}$ forming an angle of $\theta$ is given by \[R=\sqrt{A^2+B^2+2AB\cos\theta}\] where $A$ and $B$ are the magnitudes. Substituting the known data into it and solving for the unknown angle $\theta$, we will have \begin{gather*} R=\sqrt{A^2+B^2+2AB\cos\theta}\\\\ d\sqrt{3}=\sqrt{d^2+(2d)^2 +2(d)(2d)\cos\theta}\\\\ 3d^2 =d^2+4d^2+4d^2\cos\theta \\\\ -2d^2 =4d^2 \cos\theta \\\\ \Rightarrow \cos\theta =-\frac 12 \\\\ \Rightarrow \boxed{\theta=120^\circ=\frac{2\pi}{3}}\end{gather*} Where in the second equality, both sides were squared.
Hence, the correct answer is c.
Problem (8): Use all the information provided by the graph below and find the magnitude and direction (with $+x$ axis) of vector $\vec{C}=\vec{A}-\vec{B}$.
(a) $6.1\quad, 215^\circ$ (b) $5.3\quad, 135^\circ$
(c) $4\quad, 25^\circ$ (d) $6.1\quad, -26.6^\circ$
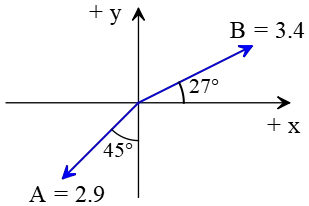
Solution: To find the subtraction of two vectors, knowing their magnitude and direction, you must first resolve those into their components. Then, algebraically subtract them to find the result.
The components of $\vec{A}$ and $\vec{B}$ are found to be \begin{align*} A_x&=A\sin 45^\circ\\&=2.9\times \frac{\sqrt{2}}2\\&=2 \\\\ A_y&=A\cos 45^\circ\\&=2.9\times \frac{\sqrt{2}}2\\&=2\\\\ B_x &=B\cos 27^\circ\\&=3 \\\\ B_y&=B\sin 27^\circ\\&=1.5\end{align*} Note that the vector $\vec{A}$ lies in the third quadrant, so all its components are toward the negative $x$ and $y$ axes. Hence, its correct components are $\vec{A}=(-2,-2)$. Now we must form the subtraction vector of two vectors $\vec{A}$ and $\vec{B}=(3,1.5)$, by subtracting the corresponding components as below \begin{align*} C_x&=A_x-B_x\\&=-2-3\\&=-5 \\\\ C_y&=A_y-B_y\\&=-2-1.5\\&=-3.5 \end{align*} Thus, these are the components of the subtraction vector whose magnitude is also found as \[C=\sqrt{C_x^2+C_y^2}=\sqrt{(-5)^2+(-3.5)^2}=\boxed{6.1}\] Given the components of a vector, one can use the following formula to find the angle that the vector makes with the positive $x$ direction \begin{align*} \alpha&=\tan^{-1}\left(\frac{C_y}{C_x}\right) \\\\&=\tan^{-1}\left(\frac{-3.5}{-5}\right) \\\\&=35^\circ \end{align*} But note that the components of $\vec{C}=(-5,-3.5)$ are in the third quadrant, so we must add $180^\circ$ to this angle to get the correct angle. Hence, \[\alpha= 180^\circ+(35^\circ)=\boxed{215^\circ}\] The correct answer is a.
Problem (9): Two vectors are given as below \begin{gather*} \vec{A}=-3\,\hat{i}+2\,\hat{j}+3\,\hat{k}\\ \vec{B}=\hat{i}+2\,\hat{k}\end{gather*} The dot product $\vec{A}\cdot \vec{B}$ equals
a. 2 b. 3 c. 4 d. 1
Solution: Assume the components of two vectors are given as $\vec{A}=(A_x, A_y , A_z)$ and $\vec{B}=(B_x,B_y,B_z)$. Their dot (scalar) product is defined as follows \[\vec{A}\cdot\vec{B}=A_xB_x+A_y B_y+A_z B_z\] In this case, we have \begin{align*}\vec{A}\cdot\vec{B}&=(-3)(1)+(2)(0)+(3)(2)\\&=\boxed{3}\end{align*} Note that the dot product of two vectors is just a number, not another vector.
Thus, the correct answer is b.
Problem (10): What is the angle between the two vectors $\vec{A}=4\,\hat{i}+4\,\hat{j}$ and $\vec{B}=3\,\hat{i}-3\,\hat{j}$ in radians?
(a) $\pi$ (b) $\frac{\pi}{2}$
(c) $\frac{3\pi}{3}$ (d) $\frac{3\pi}{4}$
Solution: The angle between two vectors $\vec{A}$ and $\vec{B}$ is found using another definition of scalar (dot) product as below \[\cos\theta=\frac{\vec{A}\cdot \vec{B}}{|\vec{A}||\vec{B}|}\] On the other side, recall that \[\vec{A}\cdot\vec{B}=A_x B_x +A_y B_y\] Thus, we have \begin{align*} \cos\theta &=\frac{(4)(3)+(4)(-3)}{\sqrt{4^2+4^2}\sqrt{3^2+(-3)^2}}\\\\ &=\frac{12-12}{4\sqrt{2}\times 3\sqrt{2}}\\\\ &=0\end{align*} Take the inverse cosine of both sides above to find the desired angle \[\theta=\cos^{-1}(0)=\frac{\pi}{2}\] Hence the correct answer is b.
Problem (11): Two vectors $\vec{A}=10\,\hat{i}-6\,\hat{j}$ and $\vec{B}=-16\,\hat{j}$ are given. What angle does the vector $\vec{C}=\vec{A}-\vec{B}$ make with the positive $x$ axis?
a. $30^\circ$ b. $60^\circ$
c. $90^\circ$ d. $45^\circ$
Solution: We are given two vectors in components form as $\vec{A}=(10,-6)$ and $\vec{B}=(0,-16)$. First, construct the subtraction vector $\vec{C}$ as below \begin{align*} C_x &=A_x-B_x\\&=10-0\\&=10 \\\\ C_y&=A_y-B_y\\&=-6-(-16)\\&=10\end{align*} Thus, $\vec{C}=(10,10)$. The angle of a vector with the positive $x$ axis, provided its components are known, is obtained by the following formula \begin{align*}\theta&=\tan^{-1}\left(\frac{C_y}{C_x}\right)\\\\&=\tan^{-1}\left(\frac{10}{10}\right)\\\\ &=\tan^{-1}(1)\end{align*} We know that the angle whose tangent is $1$ is $\boxed{45^\circ}$.
The correct answer is d.
Problem (12): The vector $\vec{A}=2\sqrt{3}\hat{i}+2\hat{j}$ is perpendicular to which of the vectors $\vec{B}=3\sqrt{3}\hat{i}-3\hat{j}$ and $\vec{C}=3\hat{i}-3\sqrt{3}\hat{j}$.
a. Only $B$ b. Only $C$
c. Both $B$ and $C$ d. None of the above.
Solution: Two vectors $\vec{A}=A_x \hat{i}+A_y \hat{j}$ and $\vec{B}=B_x \hat{i}+B_y \hat{j}$ are perpendicular to each other when their scalar product is zero \begin{gather*} \vec{A}\cdot\vec{B}=0\\ A_x B_x +A_y B_y =0 \end{gather*} So, first check the two vectors $\vec{A}$ and $\vec{B}$ \begin{align*} \vec{A}\cdot\vec{B}&=(2\sqrt{3})(3\sqrt{3})+(2)(-3)\\ &\neq 0 \end{align*} Thus, these two vectors are not perpendicular. Now check $\vec{A}$ and $\vec{C}$. \begin{align*} \vec{A}\cdot\vec{C}&=(2\sqrt{3})(3)+(2)(-3\sqrt{3})\\ &=0 \end{align*} So, these two vectors are perpendicular.
Hence, the correct answer is b.
Problem (13): What angle does vector $\hat{i}+\sqrt{3}\,\hat{j}$ make with vector $-\sqrt{3}\,\hat{i}$?
(a) zero (b) $\frac{\pi}{3}$
(c) $\frac{2\pi}{3}$ (d) $\frac{5\pi}{6}$
Solution: Consider two vectors $\vec{A}=(A_x,A_y)$ and $\vec{B}=(B_x,B_y)$. Scalar or dot product definition gives us the angle between these two vectors as \[\cos\theta=\frac{A_xB_x+A_y B_y}{AB}\] where $A$ and $B$ are the magnitudes of the vectors.
In this problem, assume $\vec{A}=(1,\sqrt{3})$ and $\vec{B}=(-\sqrt{3},0)$. Their magnitudes are \begin{align*} A&=\sqrt{A_x^2+A_y^2}\\ &=\sqrt{1^2+(\sqrt{3})^2}\\&=2 \\\\ B&=\sqrt{(-\sqrt{3})^2+0^2}\\&=\sqrt{3}\end{align*} Therefore, the angle between them is calculated as \begin{align*}\cos\theta &=\frac{(1)(-\sqrt{3})+(0)(\sqrt{3})}{2\times \sqrt{3}}\\\\&=\frac{-1}{2}\end{align*} Taking the inverse cosine of both sides gives us the desired angle \[\theta=\cos^{-1}\left(\frac{-1}{2}\right)=\frac{2\pi}{3}\] Thus, the correct angle is (c).
Problem (14): Which of the following vectors is perpendicular to the vector $\vec{a}=-2\,\hat{i}+3\,\hat{j}$?
a. $3\,\hat{i}+3\,\hat{j}$ b. $-\hat{i}+5\,\hat{j}$
c. $-3\,\hat{i}+2\,\hat{j}$ d. $3\,\hat{i}+2\,\hat{j}$
Solution: When the dot product of two vectors becomes zero, those vectors are perpendicular (the angle between them is $90^\circ$), to each other. Having the components of a vector, we can write the dot product between them as below \[ \vec{a}\cdot\vec{b}=a_x b_x+a_y b_y\] In this problem, we must check each choice separately.
a. This is false since \[(-2)(3)+(3)(3)=3\neq 0\]
b. False \[(-2)(-1)+(3)(5)=18\neq 0\]
c. False \[(-2)(-3)+(3)(2)=12 \neq 0\]
d. Correct \[(-2)(3)+(3)(2)=0 \] Hence, the correct answer is (d).
Problem (15): Consider the vector $\vec{A}=0.5\,\hat{i}-\frac 23\,\hat{j}$. What is the magnitude of the vector $6\vec{A}$?
a. -1 b. +1 c. 5 d. $\sqrt{7}$
Solution: The purpose of this problem is to explore the concept of multiplying a vector by a scalar. If a vector with components $\vec{A}=(A_x,A_y)$ is given, then the vector $\vec{B}=k\vec{A}$, where $k$ is some number, is constructed as below \[\boxed{\vec{B}=(kA_x,kA_y)}\] Thus, in this case, we will have \[6\vec{A}=6(0.5,-\frac 23)=(3,-4)\] Its magnitude is also determined using the Pythagorean theorem \[\sqrt{3^2+(-4)^2}=5\] The correct answer is c.
Problem (16): Two vectors are given as below: \begin{gather*} \vec{A}=3\,\hat{i}+2\,\hat{j}-\hat{k}\\\\\vec{B}=-2\,\hat{i}+4\,\hat{k}\end{gather*} What is the magnitude of the cross product $\vec{A}\times\vec{B}$?
Solution: There are two methods to solve cross-product problems in the AP Physics exams. One is using the definition of cross product as below which only gives us its magnitude \[|\vec{A}\times\vec{B}|=AB\sin\theta\] and the next, using the determinants, which is a bit difficult but, in turn, gives the vector itself. We chose the first method.
In the above $|\cdots|$ denotes the magnitude of the cross product.
To use the definition of the cross product, you must know the angle $\theta$ between the given vectors. In the previous problems, you learned how to find the angle between two arbitrary vectors using the dot product. So, that angle is obtained as \begin{align*} \cos\theta&=\frac{A_xB_x+A_yB_y+A_zB_z}{AB}\\\\&=\frac{(3)(-2)+(2)(0)+(-1)(4)}{\sqrt{14}\sqrt{20}}\\\\ &=\frac{-10}{\sqrt{14\times 20}}\end{align*} Taking the inverse cosine of both sides, get \[\boxed{\alpha=126.7^\circ}\] where $A$ and $B$ are the magnitudes of the given vectors. Now that the angle is known, we can simply use the cross-product definition to find its magnitude as \begin{align*} |\vec{A}\times\vec{B}|&=AB\sin\theta\\&=\sqrt{14}\sqrt{20}\sin 126.7^\circ\\&=\boxed{13.4}\end{align*}
Problem (17): Three vectors are shown in the figure below. The number next to each vector and between two adjacent vectors represent the magnitude and angle, respectively. Use this information to find the magnitude and direction of the following cross products: (a) $\vec{A}\times\vec{B}$, (b) $\vec{B}\times \vec{C}$.

Solution: The cross product of two vectors $\vec{A}$ and $\vec{B}$ is another vector at the right angle (or, perpendicular) to both. The magnitude of this vector is calculated using the formula \[|\vec{A}\times\vec{B}|=AB\sin\theta\] where $\theta$ is the acute angle (the smallest) between the two vectors.
The direction of the cross product is found using the right-hand rule. According to this rule, point the fingers of your right hand along the first vector $\vec{A}$ and turn those to the next vector $\vec{B}$. In this way, your thumb is directed along the direction of $\vec{A}\times \vec{B}$.
(a) In this case, $\theta=42^\circ$. Using the equation for the cross product above, the magnitude is \begin{align*} |\vec{A}\times\vec{B}|&=AB\sin\theta \\ &=(3)(6) \sin 42^\circ\\&=12 \end{align*} According to the right-hand rule prescription, the direction is into the page.
(b) The angle is $77^\circ+42^\circ=119^\circ$, so \begin{align*} |\vec{B}\times\vec{C}|&=BC\sin\theta \\ &=(3)(7) \sin 119^\circ\\&=18.3 \end{align*} Its direction is also out of the page.
Refer to the page below to practice more problems on the right-hand rule.
Right-hand rule: example problems
Problem (18): Five equal-magnitude forces apply to an object. If the magnitude of each force is $F$, find the resultant force vector.
a. 1F b. 2F
c. 3F d. 5F
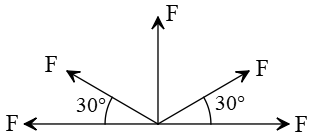
Solution: Always, the best method to find the resultant vector of a couple of vectors is to decompose all vectors along the horizontal and vertical directions, then use the rules of vector addition. Of five equal-magnitude forces, two of them are directed at an angle of $30^\circ$. So, resolve those into their components.
The force vector that is in the first quadrant has the following components \begin{gather*} F_x=F\cos 30^\circ=F\frac{\sqrt{3}}2\\\\ F_y=F\sin 30^\circ=F\left(\frac 12\right)\end{gather*}
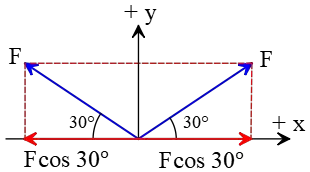
Similarly, the force in the second quadrant has the same components, but with a small difference. The $x$-component of this vector is to the left, so its correct component is $-F\frac{\sqrt{3}}2$.
Now that all vectors have been decomposed along the $x$ and $y$ axes, in each direction, algebraically add them to find the component of the resultant vector in that direction. In the $x$-direction, we have \[F\frac{\sqrt{3}}2+F-F\frac{\sqrt{3}}2-F=0\] In the $y$-direction, \[F+F\frac 12+F\frac 12=2F\] Therefore, the resultant vector $\vec{R}$ has the following components \[\vec{R}=(0,2F)\] Its magnitude is also \begin{align*}R&=\sqrt{R_x^2+R_y^2}\\&=\sqrt{0^2+(2F)^2}\\&=\boxed{2F}\end{align*} Thus, the correct answer is b.
Problem (19): What is the resultant of the forces shown in the figure below?
a. 28 b. $12\sqrt{2}$ c. $15\sqrt{2}$ d. 20
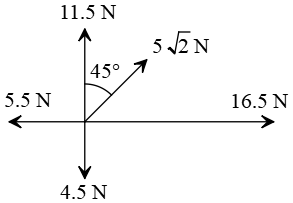
Solution: First of all, resolve the angled vector into its components along the positive $x$ and $y$ axes. Recall that a vector of magnitude $A$ that makes an angle of $\theta$ with the positive $x$ axis has a component of $A\cos\theta$ along the $x$ axis, and a component of $A\sin\theta$ along the $y$ axis.
In this problem, the tilted vector has a magnitude of $5\sqrt{2}$ and an angle of $45^\circ$ with the horizontal. So, its components are \begin{align*} A_x&=5\sqrt{2}\cos 45^\circ\\&=5\sqrt{2}\times \sqrt{2}/2 \\&=5 \\\\ A_y&=5\sqrt{2}\sin 45^\circ \\&=5\end{align*}
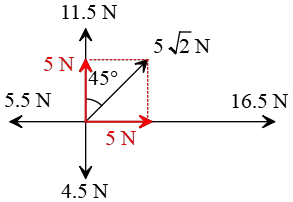
Now we have several vectors in each direction of the coordinate system. The resultant vector of a couple of vectors is defined as their vector addition. To find it, we proceed as below:
Stage (I): Add vectors lying in each direction.
Along $+x$: $16.5+5=21.5\,{\rm N}$
Along $-x$: $5.5\,{\rm N}$
Along $+y$: $11.5+5=16.5\,{\rm N}$
Along $-y$: $4.5\,{\rm N}$
Stage (II): Along each direction, subtract the vectors in the negative direction from the positive one. This gives the components of the resultant (net) vector along that direction. \begin{gather*} R_x = 21.5-5.5=16\,{\rm N} \\ R_y=16.5-4.5=12\,{\rm N}\end{gather*} where we called the resultant's components as $R_x$ and $R_y$. Thus, the resultant vector is written as \[\vec{R}=16\,\hat{i}+12\,\hat{j}\] The magnitude of a vector is also found using the Pythagorean theorem \begin{align*} R&=\sqrt{R_x^2 +R_y^2}\\\\&=\sqrt{16^2+12^2}\\\\&=\boxed{20\,{\rm N}}\end{align*} Hence, the correct answer is d.
Problem (20): What is the magnitude and direction of the resultant vector of the following vectors shown in the diagram below? (Take $\cos 53^\circ=0.6$ and $\sin 53^\circ=0.8$).
a. $2\,{\rm N}$ due west b.$2\,{\rm N}$ due east
c. $1\,{\rm N}$ due east d. $1\,{\rm N}$ due west
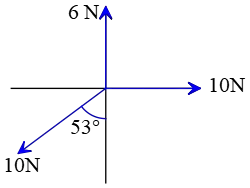
Solution: There are two vectors directed due east and north, respectively. The $10\,{\rm N}$ vector is also directed $53^\circ$ west of south. Resolve this tilted vector into its components along the $x$ and $y$ directions. \begin{align*} A_x&=A\sin\theta \\&=10\,\sin 53^\circ\\&=8 \\\\ A_y&=A\cos\theta\\&=10\,\cos 53^\circ\\&=6\end{align*}
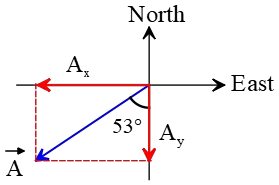
Now, along each direction, there are two vectors in opposite directions. So subtract them to find the net vector in that direction. \begin{gather*} R_x=10-8=2\,{\rm N}\\\\ R_y=6-6=0\end{gather*} These are the components of the resultant vector whose magnitude gets as \[R=\sqrt{R_x^2+R_y^2}=\sqrt{2^2+0^2}=2\,{\rm N}\] The angle that a vector makes with the positive $x$-axis is also found by \[\alpha=\tan^{-1}\left(\frac{R_y}{R_x}\right)\] So, substituting the components gives us \[\alpha=\tan^{-1}\left(\frac{0}{2}\right)=0^\circ\] Hence, the resultant vector lies toward the east and has a magnitude of $2\,{\rm N}$.
The correct answer is b.
Problem (21): As shown in the free-body diagram below, a body is subjected to three forces. The body is in equilibrium condition. Find the magnitude and direction (the angle $\theta$) of the vector $\vec{F}$
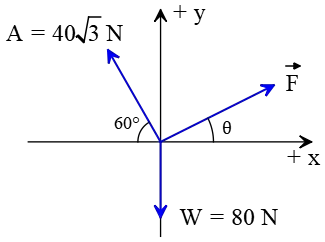
Solution: ''Equilibrium'' means that the resultant or net force on the object is zero. Three forces are acting on the body. First, resolve the tilted force vectors, find their vector addition (resultant vector), and then set it to zero.
The vector $\vec{F}$ is resolved into its components as below \begin{gather*} F_x=F\cos\theta \\F_y=F\sin\theta\end{gather*} Similarly, the components of $40\sqrt{3}-{\rm N}$ vector are \begin{align*} A_x&=A\cos 60^\circ\\&=40\sqrt{3}\left(\frac{1}{2}\right)\\&=20\sqrt{3}\,{\rm N}\\\\ A_y&=A\sin 60^\circ\\&=40\sqrt{3}\times \frac{\sqrt{3}}{2}\\&=60\,{\rm N}\end{align*} The algebraic addition of vectors along the $x$ direction gives the $x$ component of the resultant vector \[R_x=F\cos\theta-20\sqrt{3}\] Similarly, the $y$ component of the resultant vector is also found as \[R_y=F\sin\theta+60-80\] Since the object is in equilibrium, the net force on it must be zero. Thus, equate those components to zero \begin{gather*} R_x=0 \Rightarrow F\cos\theta=20\sqrt{3} \\\\\ R_y=0 \Rightarrow F\sin\theta=20\end{gather*} By dividing them, one of the unknowns, $F$, is removed. This way, the other unknown, $\theta$, is found. \begin{gather*} \frac{F\cos\theta}{F\sin\theta}=\frac{20\sqrt{3}}{20}\\\\ \Rightarrow \cot\theta =\sqrt{3} \\\\ \Rightarrow\quad \boxed{\theta=30^\circ}\end{gather*} Now, substitute the obtained angle into one of the equations $R_x=0$ or $R_y=0$ and solve for $F$. \begin{gather*}R_x=F\cos \theta-20\sqrt{3}=0\\ F\cos 30^\circ=20\sqrt{3} \\\Rightarrow \boxed{F=40\,{\rm N}}\end{gather*} where we set $\cos 30^\circ=\frac{\sqrt{3}}2$.
Problem (22): In the figure below, the rope $OB$ is horizontal, and the tension force in the rope $OA$ equals $60\sqrt{2}$. The system is in equilibrium. What is the mass of the hanging object?
a. $\sqrt{2}$ b. $6$ c. $3\sqrt{2}$ d. $3$
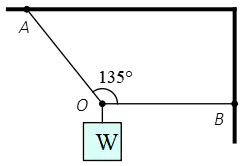
Solution: This setup is in equilibrium, so the net or resultant force on the body must be zero. Three forces are acting on the block. Two tension forces in the ropes and one weight force.
The tension force in the rope $OA$, $T_1$, is directed at an angle of $180^\circ-135^\circ=45^\circ$ with the horizontal as shown in the free-body diagram below. Resolve this tension into its components, then find the net force vector resulting from these three forces.
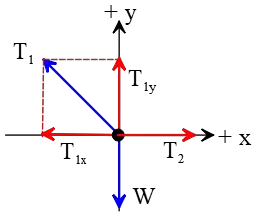
The components of the tension force $T_1$ are found to be \begin{align*} T_{1x}&=T_1\cos 45^\circ\\&=60\sqrt{2}\times \frac{\sqrt{2}}2\\&=60\,{\rm N}\\\\T_{1y}&=T_1\sin 45^\circ\\&=60\sqrt{2}\times \frac{\sqrt{2}}2\\&=60\,{\rm N}\end{align*} The object does not move vertically, so the net force in this direction must be zero, i.e., $T_{1y}=W$. Therefore, we have \[T_{1y}=W \Rightarrow W=60\,{\rm N}\] Using the definition of weight as $W=mg$, the mass of the object is \[m=\frac{W}{g}=\frac{60}{10}=6\,{\rm kg}\] Hence, the correct answer is b. (Find the tension in the rope $OB$.)
Problem (23): If the resultant of the following three vectors is zero, find $a$ and $b$, respectively.
\begin{gather*} \vec{A}=3\,\hat{i}+2\,\hat{j}\\ \vec{B}=-5\,\hat{i}+3\,\hat{j}\\\vec{C}=a\,\hat{i}+b\,\hat{j}\end{gather*}
Solution: In all the AP Physics exams, the resultant vector means the addition of vectors. We call it $\vec{R}$. So, we must find the addition of the three above vectors, set it to zero, and solve the obtained equations for the unknowns. \[\vec{R}=\vec{A}+\vec{B}+\vec{C}=0\] We summarize each vector as below for simplicity \[\vec{A}=(3,2) \, , \vec{B}=(-5,3) \, , \vec{C}=(a,b)\] By adding the corresponding components with each other, we will have \begin{align*} R_x &=3+(-5)+a\\R_y &= 2+3+b \end{align*} These are the components of the resultant vector, setting these to zero yields \begin{gather*} R_x=0 \Rightarrow \boxed{a=2} \\ R_y=0 \Rightarrow \boxed{b=-5} \end{gather*}
Author: Dr. Ali Nemati
Page Published: 10/19/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
