Vector Practice Problems in Physics for High Schools
A set of practice problems on vectors that appear in physics courses are collected. Designed specifically for high school and college students, these straightforward problems are aimed at helping you strengthen your understanding of vector concepts.
Vector Problems
Problem (1): Find the x and y components of the following vectors in physics
(a) A 10-m displacement vector that makes an angle of $30^\circ$ with the $+x$ direction.
(b) A 20-m/s velocity vector that makes an angle of $37^\circ$ counterclockwise from the $-x$ direction.
(c) An 80-N force vector that makes an angle of $135^\circ$ counterclockwise from the $-y$ direction.
Solution: The length and direction (angle) of a vector are given. Recall that with this information, we can relate them to the components of a vector using the following formulas: \begin{gather*} R_x=|\vec{R}|\cos\theta\\ R_y=|\vec{R}|\sin\theta\end{gather*} Where $\theta$ is the angle that the vector $\vec{R}$ makes with the positive $x$ axis and is measured in a counterclockwise direction.
(a) Here, the components are: \begin{align*}R_x&=|\vec{R}|\cos\theta\\&=(10)\cos 30^\circ\\&=5\sqrt{3}\quad {\rm m}\\\\R_y&=|\vec{R}|\sin\theta\\&=(10)\sin 30^\circ\\&=5\quad {\rm m}\end{align*}
(b) In this section, the angle with the negative x-axis is given as shown in the figure. To measure it from the $+x$ axis in the counterclockwise direction, we must add it to $180^\circ$. Therefore, the final angle is $180^\circ+37^\circ=217^\circ$. The components are: \begin{align*}v_x&=|\vec{v}|\cos\theta\\&=(20)\cos 217^\circ\\&=-16\quad {\rm m/s}\\\\v_y&=|\vec{v}|\sin\theta\\&=(20)\sin 217^\circ\\&=-12\quad {\rm m/s}\end{align*}
(c) Here, the direction of the force vector is measured from the $-y$ direction as shown in the figure below. As you can see, the vector makes an angle of $45^\circ$ with the $+x$ axis in the counterclockwise direction.
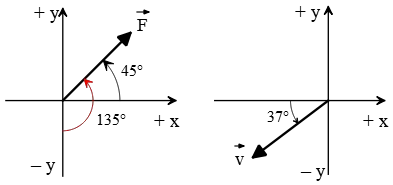
The components are not given, but we can find them using the following formulas: \begin{align*}F_x&=|\vec{F}|\cos\theta\\&=(80)\cos 45^\circ\\&=40\sqrt{2}\quad {\rm N}\\\\F_y&=|\vec{F}|\sin\theta\\&=(80)\sin 45^\circ\\&=40\sqrt{2}\quad {\rm N}\end{align*}
Problem (2): A vector has an x-component of -10 units and y-components of 13 units. Find the magnitude and direction of the vector.
Solution: The components of a vector, denoted as $\vec{A}$, are related to the magnitude and direction of the vector by the following formula: \begin{align*} |\vec{A}|&=\sqrt{A_x^2+A_y^2}\\&=\sqrt{(-10)^2+(13)^2}\\&=16.4\\\\ \theta&=\arctan\frac{A_y}{A_x}\\&=\arctan\frac{13}{-10}\\&=-52^\circ\end{align*} It is important to note that there is a subtle point about the formula for the vector direction.
If the vector lies in the first or fourth quadrant, then the angle obtained from the above formula is correct. However, if the vector lies in the second or third quadrant, we must add $180^\circ$ to the angle obtained from the formula to obtain the correct angle.

Here, the components show that the original vector lies in the second quadrant, so the correct angle with the $+x$-axis in a counterclockwise direction (the standard angle measured for a vector) is obtained as below \[\alpha=180^\circ-52^\circ=128^\circ\] Consequently, the vector has a length of 16.4 units and makes an angle of $128^\circ$ with the $+x$-axis.
Problem (3): In each of the following cases, the components of the vectors are given. Write each vector in terms of its magnitude and direction.
(a) A velocity vector with an x component of -2.5 m/s and a y component of +3 m/s.
(b) A Displacement in the third quadrant with an x component of 1 m and a y component of 2.7 m.
Solution: We can use the Pythagorean theorem and the tangent function to relate the components of a vector, say $\vec{A}$, to its magnitude and direction with the following equations: \begin{gather*} |\vec{A}|=\sqrt{A_x^2+A_y^2} \\ \theta=\arctan\frac{A_y}{A_x}\end{gather*}
(a) The components of the velocity vector are $v_x=-2.5\,{\rm m/s}$ and $v_y=+3\,{\rm m/s}$. The magnitude and direction of this vector are found as \begin{align*} |\vec{v}|&=\sqrt{v_x^2+v_y^2}\\&=\sqrt{(-2.5)^2+3^2}\\&=3.9\quad {\rm m/s} \\\\ \theta&=\arctan\frac{v_y}{v_x}\\&=\arctan\frac{+3}{-2.5}\\&=-50.2^\circ\end{align*} Since the vector lies in the second quadrant, we must add $180^\circ$ to the answer obtained from the above vector direction formula which gives \[\alpha=180^\circ-50.2^\circ=129.8^\circ\]
(b) Because the vector lies in the third quadrant, its $x$ and $y$ components must be negative as $d_x=-1\,{\rm m}$ and $d_y=-2.7\,{\rm m}$. Therefore, by knowing the components, the magnitude and direction of the displacement vector are computed as below \begin{align*} |\vec{D}|&=\sqrt{d_x^2+d_y^2}\\&=\sqrt{(-1)^2+(-2.7)^2}\\&=2.8\quad {\rm m} \\\\ \theta&=\arctan\frac{d_y}{d_x}\\&=\arctan\frac{-2.7}{-1}\\&=69.6^\circ\end{align*} Because the vector is in the third quadrant, so add $180^\circ$ to the above angle to get the correct angle as below \[\alpha=180^\circ+69.6^\circ=249.6^\circ\]
Problem (4): A cannonball is fired at an angle of $37^\circ$ with a speed of $100\,{\rm m/s}$. What is the component of the cannonball's velocity with the horizontal?
Solution: All thing given is a description of a vector in physics called velocity. Recall that the velocity vector has a magnitude, called speed, and a direction.
In this example, the magnitude, $|\vec{v}|=100\,{\rm m/s}$, and direction, $\theta=37^\circ$, of a vector are given and wants its components.
The $x$ component of the vector is found by the following formula \begin{align*} \vec{v}_x&=|\vec{v}|\cos \theta\\&=100\times \cos 37^\circ\\&=100\times 0.8 \\&=80\quad {\rm m/s}\end{align*} Indeed, these kinds of vectors, are used frequently in projectile motion problems.
If you want to solve more problems on the projectile motion refer to the following page:
Problems on projectile motion
Problem (5): Find a unit vector $\hat{u}$ in the direction of the vector $\vec{w}=3\hat{i}+11\hat{j}$.
Solution: If all components of a vector are divided by its magnitude, then by definition, a unit vector in the direction of the original vector is constructed.
The magnitude of the given vector is computed as \[|\vec{w}|=\sqrt{3^2+11^2}=\sqrt{130}\] Therefore, the unit vector is found as below \begin{align*} \hat{u}&=\frac{\vec{w}}{|\vec{w}|}\\\\&=\frac{(3,11)}{\sqrt{130}}\\\\&=\left(\frac{3}{\sqrt{130}},\frac{11}{\sqrt{130}}\right)\end{align*} One of the main properties of unit vectors is that its magnitude must be 1.
You can check that the unit vector obtained above satisfies this condition.
There are also more solved problems about unit vectors that you must see.
Vector Word Problems
Problem (6): A cruise ship travels 200 km due east from point A to B and then 300 km due south from B to the final destination, point C. (a) Write the displacement vector in component form. (b) How far is the direct distance between A to C? (c) What angle does the displacement vector make with the positive $x$-axis?
Solution: The goal is to find the displacement between start to finish. There are two methods to achieve this.
One is using the graphical method and applying the Pythagorean theorem to find the hypotenuse of the right triangle (which is the direct distance) as the figure below.
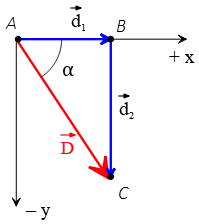
The second is using vectors in component form as follows.
(a) The expression of 200 km due east in vector language is written as $\vec{d}_1=200\,\hat{i}$ and similarly, 300 km due south is $\vec{d}_2=-300\,\hat{j}$. Adding the above vectors yields the displacement vector \begin{align*} \vec{D}&=\vec{d}_1+\vec{d}_2\\&=200\,\hat{i}-300\,\hat{j}\end{align*}
(b) The direct distance across the whole path is found by calculating the magnitude of the displacement vector. Therefore, \begin{align*} |\vec{D}|&=\sqrt{D_x^2+D_y^2}\\&=\sqrt{(200)^2+(-300)^2}\\&=500\quad {\rm km}\end{align*}
(c) The angle that a vector makes with the $+x$ axis in the counterclockwise direction is found by the formula below \begin{align*} \alpha&=\tan^{-1}\left(\frac{D_y}{D_x}\right)\\\\&=\tan^{-1}\left(\frac{-300}{200}\right)\\\\&=-56.3^\circ\end{align*} Note that this formula does not give always the correct angle!
If the vector lies in the first and fourth quadrant, then this gets the correct angle but for vectors in the second and third quadrant, we must add $180^\circ$ to the angle obtained by the formula above. In this way, you will always get the right angle.
Here, the resultant vector lies in the fourth quadrant so the negative in the angle obtained above indicates that it is below the positive $x$-axis.
Problem (7): A plane flies from point A to B, a distance of 300 km in the direction of $32^\circ$ east of north. After military operations, the plane flies to point C which is 340 km away and $63^\circ$ west of north. (a) Write each displacement in vector components form. (b) Find the displacement and direction from start to finish. (c) What is the total distance traveled by plane?
Solution: The magnitude and direction of each flight path were given. Each direct path is assumed as a vector. In this problem, pay attention to the given angles.
The angle in the formula of decomposition of a vector into its components is measured from the $+x$-axis in a counterclockwise direction. \begin{gather*} A_x=|\vec{A}|\cos\theta\\A_y=|\vec{A}|\sin\theta\end{gather*} Here, the east of north means that you first stand facing to the north, then move as much as $32^\circ$ to the east. But this angle is measured from the +y direction in the CW direction. To convert it from the +x axis, we have $90^\circ-32^\circ=58^\circ$.
Similarly, $63^\circ$ west of north corresponds to $90^\circ+63^\circ=153^\circ$ measured from the $+x$-axis in a CCW direction (figure below).
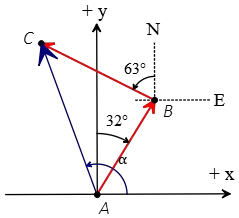
(a) With this information, the components of the vectors are written as below \begin{align*} \vec{d}_{AB}&=|\vec{d}_{AB}|\cos 58^\circ\,\hat{i}+|\vec{d}_{AB}|\sin 58^\circ\,\hat{j}\\&=(300)(0.53)\,\hat{i}+(300)(0.85)\,\hat{j}\\&=159\,\hat{i}+255\,\hat{j}\end{align*} And similarly, for the second path we have \begin{align*} \vec{d}_{BC}&=|\vec{d}_{BC}|\cos 153^\circ\,\hat{i}+|\vec{d}_{BC}|\sin 153^\circ\,\hat{j}\\&=(340)(-0.9)\,\hat{i}+(340)(0.45)\,\hat{j}\\&=-306\,\hat{i}+153\,\hat{j}\end{align*} Therefore, each displacement in vector components are summarized as $\vec{d}_1=(159,255)$ and $\vec{d}_2=(-306,153)$.
(b) Total displacement is the sum of the two displacements above which is a vector addition problem. To accomplish this, we must sum the corresponding components with each other. \begin{align*} \vec{D}&=\vec{d}_1+\vec{d}_2\\&=(159,255)+(-306,153)\\&=(159-306,255+153)\\&=(-147,408)\end{align*} Therefore, the total displacement from start to finish is written like a vector as below \[\vec{D}=-147\,\hat{i}+408\,\hat{j}\] The angle that this vector makes with the positive x-axis is computed as below \begin{align*} \alpha&=\tan^{-1}\left(\frac{D_y}{D_x}\right)\\\\&=\tan^{-1}\left(\frac{408}{-147}\right)\\\\&=-70^\circ\end{align*} In this vector problem, the displacement vector lies in the second quadrant so the right angle with the positive x-axis will be obtained as \[\alpha=180^\circ-70^\circ=110^\circ\]
Problem (8): Someone kicks a soccer ball. In his first attempt, the path of the ball in two dimensions is described as $\vec{d}_1=10\hat{i}+20\hat{j}$. In the second hit, the ball follows the path of $\vec{d}_2=5\hat{i}-40\hat{j}$ in a straight line. (a) In which hit did the ball travel farther distance? (b) At what distance do the balls fall to the ground from each other?
Solution: The paths of balls are given as vectors. The magnitude of these vectors will give the distances that the balls traveled.
(a) The magnitude of the first vector is \[|\vec{d}_1|=\sqrt{10^2+20^2}=22.36\] Similarly, the magnitude of the second vector which is distance is calculated as \[|\vec{d}_2|=\sqrt{5^2+(-40)^2}=40.31\] Therefore, the ball in the second attempt has traveled more distance.
(b) The goal is to find the difference between two vectors. We do this with the help of vector components as follows \begin{align*} \vec{C}&=\vec{d}_2-\vec{d}_1\\&=(5,-40)-(10,20)\\&=(5-10,-40-20)\\&=(-5,-60)\end{align*} Therefore, the difference between the two vectors is a vector as $\vec{C}=-5\hat{i}-60\hat{j}$ whose magnitude gives the required distance. \[|\vec{C}|=\sqrt{(-5)^2+(-60)^2}=60.2\]
Problem (9): Someone walks 400 m due west, then jogs 200 m north, then walks 300 m in a direction of $30^\circ$ east of north. Determine the distance and direction of the motion from the starting point to the ending point.
Solution: The problem asks us to find the vector sum of three displacement vectors. We can start by drawing the third displacement vector as $30^\circ$ east of north. To do this, we face north and then turn $30^\circ$ to the east.
To resolve this vector into its components, we note that it makes an angle of $90^\circ-30^\circ=60^\circ$ with the positive $x$-axis in the counterclockwise direction. Using the components formula, we have: \begin{align*}\vec{d}_3&=|\vec{d}_3|\cos 60^\circ\hat{i}+\vec{d}_3\sin 60^\circ\hat{j}\\&=(300)(1/2)\hat{i}+(300)(\sqrt{3}/2)\hat{j}\\&=150\hat{i}+150\sqrt{3}\hat{j}\end{align*}
If we take east and north as the positive $x$ and $y$ axes, respectively, then the first two displacement vectors in vector form are $\vec{d}_1=-400\,\hat{i}$, $\vec{d}_2=200\,\hat{j}$.
Adding up the components of the above vectors gives the components of the total displacement vector from start to finish: \begin{align*} \vec{D}&=\vec{d}_1+\vec{d}_2+\vec{d}_3\\&=(-400,0)+(0,200)+(150,150\sqrt{3})\\&=(-400+0+150,0+200+150\sqrt{3})\\&=(-250,460)\end{align*} Therefore, the vector that shows the total displacement is written as: \[\vec{D}=-245\,\hat{i}+460\,\hat{j}\] The magnitude of the above vector gives the direct distance between the start to finish as \[|\vec{D}|=\sqrt{(-245)^2+(460)^2}=524\quad {\rm m}\] And its direction with respect to the horizontal is: \begin{align*} \theta&=\arctan\frac{D_y}{D_x}\\&=\arctan\frac{460}{-245}\\&=-62^\circ\end{align*} Since the vector lies in the second quadrant, we must add $180^\circ$ to the angle to get the correct direction: \[\alpha=180^\circ+(-62^\circ)=118^\circ\]
Problem (10): A plane is flying in the direction of $23^\circ$ west of south. After 250 km, the pilot changes its direction and flies due $30^\circ$ south of west for 200 km. What is the displacement and bearing from the starting point?
Solution: For each path, a magnitude and an angle (direction) have been given. These values are characteristics of a vector. In this case, these are displacement vectors.
To find the total displacement throughout the flight, we must first write each displacement vector in its component form and then add the corresponding components.
First, put magnitudes and directions into a coordinate system to form the vectors as in the figure below
Keep in mind that in such problems, the given angles must be measured from a reference axis in a clockwise direction. Here, we choose the positive $x$ axis as the reference.
Because it is easier to reach the $23^\circ$ west of south from the $+x$ axis in a counterclockwise direction, after adding $90^\circ$ to $23^\circ$, we must insert a negative in front of the result.
Therefore, the angles of $23^\circ$ west of south and $30^\circ$ east of south are measured from $+x$ axis as $\alpha=90^\circ+23^\circ=-113^\circ$ and $180^\circ+30^\circ=210^\circ$.
For the first flight, the components of the displacement vector are obtained as below \begin{align*} A_x&=|\vec{A}|\cos \alpha\\&=250\times \cos (-113^\circ) \\&=-97.68\quad {\rm m} \\\\ A_y&=|\vec{A}|\sin \alpha\\&=250\times \sin (-113^\circ) \\&=-230.12\quad {\rm m}\end{align*} Similarly, for the second flight, the components for the displacement vector $\vec{B}$ are \begin{align*} B_x&=|\vec{B}|\cos \theta\\&=200\times \cos (210^\circ) \\&=-173.20\quad {\rm m} \\\\ B_y&=|\vec{A}|\sin \theta\\&=200\times \sin (210^\circ) \\&=-100\quad {\rm m}\end{align*}
Now, adding the corresponding components gives the components of the displacement vector $\vec{D}$ \begin{align*} D_x&=A_x+B_x\\&=-97.68-173.20\\&=-270.88\quad {\rm m}\\\\ D_y&=A_y+B_y\\&=-230.12-100\\&=-330.12\quad {\rm m}\end{align*} Recall from physics that, the magnitude of the displacement vector is the direct distance between start and end points.
Problem (11): A ball is fired with an initial speed of 15 m/s at an angle of $37^\circ$ with the horizontal. Find the vertical and horizontal components of the velocity.
Solution: Speed and angle are the characteristics of the velocity vector in physics. The components of a vector $\vec{v}$ in the Cartesian coordinate system are found as $v_x=|\vec{v}|\cos\theta$ and $v_y=|\vec{v}|\sin\theta$ where $theta$ is measured from the positive x-axis in a clockwise direction.
Recall from physics that the magnitude of the velocity vector is called speed. With this reminder, the components of the ball's velocity are computed as below \begin{align*} v_x&=15\times \cos 37^\circ\\&=12\quad {\rm m/s}\\\\v_y&=15\sin 37^\circ\\&=9\quad {\rm m/s}\end{align*}
Problem (12): Two forces with the following properties are applied to a body. Find the resultant force, acting on the body.
Force $F_1$: 40 N at $37^\circ$ and force $F_2$: 60 N at $225^\circ$ with the positive x-axis.
Solution: The goal is to find the sum of two vectors. First, decompose the force vectors into their components, and then add the corresponding components to find the components of the resultant vector.
The components of a vector $\vec{F}$ with magnitude of $|\vec{F}|$ that makes an angle of $\theta$ with the positive x axis in a clockwise direction, is found by the following formula \begin{gather*} F_x=|\vec{F}|\cos\theta\\F_y=|\vec{F}|\sin\theta\end{gather*} The components of the forces in this problem are \begin{align*}F_{1x}&=|\vec{F}_1|\cos 37^\circ\\&=40\times 0.8\\&=32\quad {\rm N}\\\\F_{1y}&=|\vec{F}_2|\sin 37^\circ\\&=40\times 0.6\\&=24\quad {\rm N}\end{align*} And similarly, for the force vector $\vec{F}_2$ \begin{align*}F_{2x}&=|\vec{F}_2|\cos 225^\circ\\&=60\times \left(-\sqrt{2}/2\right)\\&=-30\sqrt{2}\quad {\rm N}\\\\F_{2y}&=|\vec{F}_2|\sin 225^\circ\\&=60\times \left(-\sqrt{2}/2\right)\\&=-30\sqrt{2}\quad {\rm N}\end{align*} The resultant force is the vector addition of these two vectors. Therefore, \begin{align*} F_x&=F_{1x}+F_{2x}\\&=32-30\sqrt{2}\\&=-10.42\quad {\rm N}\\\\F_y&=F_{1y}+F_{2y}\\&=24-30\sqrt{2}\\&=-18.42\quad {\rm N}\end{align*} Hence, the resultant force vector is described in a vector notation as \[\vec{F}=-10.42\hat{i}-18.42\hat{j}\] The magnitude of the net force is also computed as \[|\vec{F}|=\sqrt{(-10.42)^2+(-18.42)^2}=21.17\,{\rm N}\] The angle of the net force vector that makes with the positive x axis is found by the following formula \begin{align*} \alpha &=\tan^{-1}\frac{F_y}{F_y}\\\\&=\tan^{-1}\left(\frac{-18.42}{-10.42}\right)\\\\&=60.5^\circ\end{align*}
Problem (13): A car moving and has a bearing of $S\,29^\circ\, W$. The speed of the car is 30 km/h. How many kilometers south and how many kilometers west will the car have moved for 4 hours?
Solution: A bearing is an acute angle that a straight path makes with a fixed north-south line.
In this problem, the direction and magnitude of a vector were given but its direction is not in the standard form to resolve it into its components.
A bearing of $S\,29^\circ\, W$ means that first stands to the south and then moves at an angle of $29^\circ$ to the west as the figure below
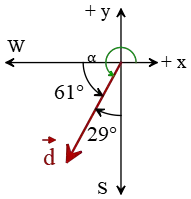
This angle is measured from the $-y$ axis. To decompose a vector, the angle must be measured from the positive $x$ axis in a counterclockwise direction.
From the $+x$ axis, we can reach the above angle in a counterclockwise direction. Thus, the angle obtained in this way is $\alpha=180^\circ+61^\circ=241^\circ$.
Using the uniform kinematic equation, $x=vt$, we can find the total distance traveled by the car in the given direction for 4 hours. \[x=(30)(4)=120\quad{\rm km}\] Therefore, the length and direction of the movement are known. Now, we can find the components of the vector, say $\vec{d}$, with these properties as below \begin{align*} d_x&=|\vec{d}|\cos \theta\\&=(120)\cos 241^\circ\\&=-58\quad {\rm km}\\\\d_y&=|\vec{d}|\sin\theta\\&=(120)\sin 241^\circ\\&=-105\quad {\rm km}\end{align*} In the above, the negatives indicate the direction of the distance traveled by the car.
Therefore, the car traveled 58 km due west and 105 km toward the south.
Summary:
In this article, a couple of questions about vectors in physics are solved. The direction and magnitude of vectors, unit vectors, and projectile motion vectors were some of the solved problems.
Author: Ali Nemati
Page Published: 6-29-2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
