Grade 12: Physics Worksheet on Projectile Motion
Looking to master projectile motion in your physics class? Check out our comprehensive worksheet with detailed solutions to help you understand the concepts and excel in your studies!
There is also a pdf for worksheets with answers.
A summary of projectile motion:
Any motion having the following conditions is called a projectile motion.
(i) Follows a parabolic path (trajectory).
(ii) Moves under the influence of gravity.
The projectile motion formulas applied to solve two-dimensional projectile motion problems are as follows \begin{gather*} x=(v_0\cos\theta)t+x_0\\\\y=-\frac 12 gt^2+(v_0\sin\theta)t+y_0\\\\ v_y=v_0\sin\theta-gt\\\\v_y^2-(v_0\sin\theta)^2=-2g(y-y_0)\end{gather*}
Projectile motion problems and answers
Problem (1): A person kicks a ball with an initial velocity of 15 m/s at an angle of 37° above the horizontal (neglecting the air resistance). Find
(a) the total time the ball is in the air.
(b) the horizontal distance traveled by the ball
Solution: The initial step in answering any projectile motion questions is to establish a coordinate system and sketch the path of the projectile, including its initial and final positions and velocities.
By doing so, you will be able to solve the relevant projectile equations easily.
Hence, we choose the origin of the coordinate system to be at the throwing point, $x_0=0, y_0=0$.

(a) Here, we are seeking the time it takes for the projectile to travel from the point of release to the ground.
In reality, projectiles have two independent motions: one in the horizontal direction with uniform motion at a constant velocity (i.e., $a_x=0$), and the other in the vertical direction under the effect of gravity (with $a_y=-g$).
The kinematic equations that describe the horizontal and vertical distances are as follows: \begin{gather*} x=x_0+(\underbrace{v_0\cos \theta}_{v_{0x}})t \\ y=-\frac 12 gt^2+(\underbrace{v_0\sin \theta}_{v_{0y}})t+y_0\end{gather*} By substituting the coordinates of the initial and final points into the vertical equation, we can find the total time the ball is in the air.
Setting $y=0$ in the second equation (because the projectile lands at the same level as the throwing point.), we have: \begin{align*} y&=-\frac 12 gt^2+(v_0\sin \theta)t+y_0\\\\ 0&=-\frac 12 (9.8)t^2+(15)\sin 37^\circ\,t+0 \end{align*} By rearranging the above expression, we can obtain two solutions for $t$: \begin{gather*} t_1=0 \\\\ t_2=\frac{2\times 15\sin37^\circ}{9.8}=1.84\,{\rm s}\end{gather*} The first time represents the starting moment, and the second represents the total time the ball was in the air.
(b) As previously mentioned, projectile motion consists of two independent motions with different positions, velocities, and accelerations, each described by distinct kinematic equations.
The time it takes for the projectile to reach a specific point horizontally is equal to the time it takes to fall vertically to that point. Therefore, time is the common factor in both the horizontal and vertical motions of a projectile.
In this particular problem, the time calculated in part (a) can be used in the horizontal kinematic equation to determine the distance traveled.
Substituting the obtained time into the equation, we find that the projectile travels a distance of 22.08 meters. \begin{align*} x&=x_0+(v_0\cos \theta)t \\ &=0+(15)\cos 37^\circ\,(1.84) \\ &=22.08\quad {\rm m}\end{align*}
Be sure to check the following questions.
If you are getting ready for the AP Physics exam, these problems on the kinematics equation (or these AP Physics Kinematics Problems) are probably also useful to you.
Problem (2): A ball is thrown into the air at an angle of 60° above the horizontal with an initial velocity of 40 m/s from a 50-m-high building. Find
(a) The time to reach the top of its path.
(b) The maximum height the ball reached from the base of the building.
Solution: In the previous question, we found that the motion of a projectile consists of two distinct vertical and horizontal movements.
We learned about how to find distances in both directions using relevant kinematic equations.
There is also another set of kinematic equations that discuss the velocities in vertical and horizontal directions as follows \begin{gather*} v_x=v_{0x}=v_0\cos\theta \\ v_y=v_{0y}-gt=v_0\sin\theta-gt\end{gather*} As you can see, the horizontal component of the velocity, $v_x$, is constant throughout the motion, but the vertical component varies with time.
As an important note, keep in mind that in the problems about projectile motions, at the highest point of the trajectory, the vertical component of the velocity is always zero, i.e., $v_y=0$.
To solve the first part of the problem, specify two points as the initial and final points, then solve the relevant kinematic equations between those points.
Here, setting $v_y=0$ in the second equation and solving for the unknown time $t$, we have \begin{align*} v_y&=v_{0y}-gt \\\\ &=v_0\sin\theta-gt \\\\ 0&=(40)(\sin 60^\circ)-(9.8)(t) \\\\ \Rightarrow t&=\boxed{3.53\, {\rm s}}\end{align*} Thus, the time taken to reach the maximum height of the trajectory (path) is 3.53 seconds from the moment of the launch. We call this maximum time $t_{max}$.
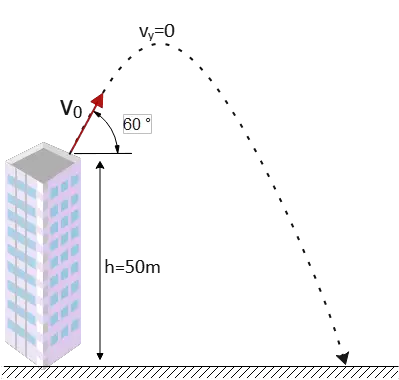
(b) Let the origin be at the throwing point, so $x_0=y_0=0$ in the kinematic equations. In this part, the vertical distance traveled to the maximum point is requested.
By substituting $t_{max}$ into the vertical distance projectile equation, we can find the maximum height as below \begin{align*} y-y_0&=-\frac 12 gt^2 +(v_0 \sin \theta)t\\ \\ y_{max}&=-\frac 12 (9.8)(3.53)^2+(40 \sin 60^\circ)(3.53)\\\\ &=61.22\quad {\rm m}\end{align*} Therefore, the maximum height at which the ball is reached from the base of the building is \[H=50+y_{max}=111.22\quad {\rm m}\]
For further reading about uniform motion along the horizontal direction, see speed, velocity, and acceleration problems.
Problem (3): A person standing on the edge of a 50-m-high cliff throws a stone horizontally at a speed of 18 m/s.
(a) What is the initial position of the stone?
(b) What are the components of the initial velocity?
(c) What are the $x$- and $y$-components of the velocity of the stone at any arbitrary time $t$?
(d) How long will it take the stone to strike the bottom of the cliff?
(e) With what angle and speed does the stone strike the ground below the cliff?
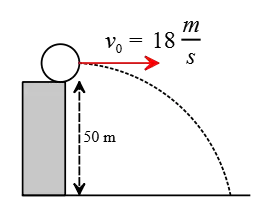
Solution: As mentioned repeatedly, as a first step to solving a projectile motion problem, choose a relevant coordinate system.
(a) Usually, we place the origin of the coordinate system at the point where the projectile is thrown. In this case, the coordinate of the initial position is $x_0=0\, , \, y_0=0$.
If we had chosen the coordinate at the base of the cliff and placed the origin at that point, the position of the initial point would have been $x_0=0\, , \, y_0=50\,\rm m$.
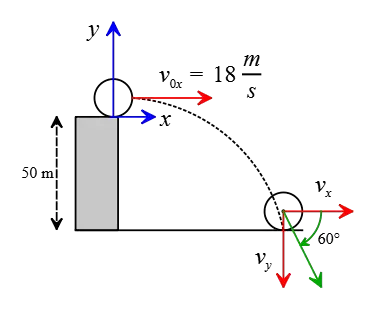
(b) The stone is thrown horizontally with $\theta=0$, so there is no vertical velocity component. Consequently, its initial speed components are $v_{0x}=18\,\rm m/s$ and $v_{0y}=0$.
(c) Remember that the velocity components of a projectile change over time according to the following formula. Substituting the given values into it, we get: \begin{align*} v_x&=v_{0x}=18\,\rm m/s \\\\ v_y&=v_{0y}-gt\\&=-9.8t \end{align*}
(d) If we take the top of the cliff to be the origin of our coordinate system, with $x_0=y_0=0$, the stone hits the ground $50\,\rm m$ below our chosen origin. Therefore, the coordinates of that point would be $x_0=?\, ,\, y=-50\,\rm m$.
Use the vertical displacement kinematic equation below, substitute the numerical values into that, and solve for time $t$ get \begin{gather*} y-y_0=-\frac 12 gt^2+v_{0y}t \\\\ -50-0=-\frac 12 (9.8)t^2-0 \\\\ \Rightarrow \quad \boxed{t=3.2\,\rm s} \end{gather*}
(e) First, find the velocity components just before the stone hits the ground. We know that it takes about $3.2\,\rm s$ for the stone to reach the bottom of the cliff. Thus, put this time value into the formulas of velocity components at any time $t$. \begin{align*} v_x&=v_{0x}=18\,\rm m/s \\\\ v_y&=v_{0y}-gt\\&=-9.8\times 3.2 \\&=-31.36\,\rm m/s \end{align*} Notice that the negative sign here indicates that the vertical velocity component just before hitting the ground points downward, as expected.
Recall from the section on vector practice problems that when we have the components of a vector, we can find its magnitude using the Pythagorean theorem. This gives us: \begin{align*} v&=\sqrt{v_x^2+v_y^2} \\\\ &=\sqrt{18^2+(-31.36)^2} \\ &=\boxed{36.15\,\rm m/s} \end{align*} We can also find the angle of impact with the ground using the velocity components: \begin{align*} \tan\theta&=\frac{v_y}{v_x} \\\\ &=\frac{-31.36}{18} \\\\ &=-1.74 \end{align*} Taking the inverse tangent of both sides gives: \[\theta=\tan^{-1}(-1.74)=\boxed{-60.1^\circ} \] Therefore, the stone hit the ground at an angle of about $60^\circ$ with a speed of $36.15\,\rm m/s$. The negative angle indicates that it is below horizontal, which is to be expected.
Problem (4): A book slides off a frictionless tabletop with a constant speed of 1.1 m/s, and 0.35 seconds later strikes the floor.
(a) How high is the tabletop from the floor?
(b) What is the horizontal distance to that point where the book strikes the floor?
(c) How fast and at what angle does the book strike the floor?
Solution: The total time the book is in the air is $t=0.35\,\rm s$, and the initial speed with which the book leaves the table horizontally is $v_{0x}=1.1\,\rm m/s$, and $v_{0y}=0$.
Contrary to the earlier question, in this case, for practice, we place the origin at the bottom of the tabletop. Thus, the coordinates of the initial position would be $x_0=0\, ,\, y_0=h=?$ and the coordinates of the landing point would be $x=? \, , \, y=0$.
(a) If we substitute the given values into the vertical displacement kinematic equation, we will have \begin{gather*} y-y_0=-\frac 12 gt^2+v_{0y}t \\\\ 0-h=-\frac 12 (9.8)(1.1)^2+0 \\\\ \Rightarrow \quad \boxed{h=5.93\,\rm m} \end{gather*} Thus, the table is 3-m-high.
(b) Remember that projectile motion involves two motions that are uniformly accelerated in the horizontal and vertical directions. The time taken by the projectile in the vertical direction is equal to the horizontal time to the landing point.
Between the start and final points in the horizontal direction of the projectile path, we can write $\Delta x=v_{0x}t$. Substituting the given values into is get \begin{gather*} x-0=1.1\times (0.35) \\ \Rightarrow \quad \boxed{x=0.385\,\rm m} \end{gather*} where $\Delta x=x-x_0$. Therefore, the book strikes the floor about $39\,\rm cm$ ahead of the base of the table.
(c) This part is straightforward. Substitute the given numerical values into the velocity vector component formulas as below to find the velocity components just before the book strikes the floor. \begin{align*} v_x&=v_{0x}=1.1\,\rm m/s \\\\ v_y&=v_{0y}-gt \\\\ &=0-(9.8)(0.35) \\&=-3.43\,\rm m/s \end{align*} The square root of the sum of the velocity components squared gives the velocity of the book at the instant of hitting \begin{align*} v&=\sqrt{v_x^2+v_y^2} \\\\ &=\sqrt{1.1^2+(-3.43)^2} \\\\ &=\boxed{3.6\,\rm m/s} \end{align*} and angle of impact with the ground is found as below \begin{align*} \theta&=\tan^{-1}\left(\frac{v_y}{v_x}\right) \\\\ &=\tan^{-1}\left(\frac{-3.43}{1.1}\right) \\\\ &=\tan^{-1}(-3.11) \\\\&=\boxed{-72.17^\circ} \end{align*} Overall, the book hit the ground at an angle of about $72^\circ$ with a speed of nearly $3.6\,\rm m/s$.
Problem (5): A cannonball is fired from a cliff with a speed of 800 m/s at an angle of 30° below the horizontal. How long will it take to reach 150 m below the firing point?
Solution: First, choose the origin to be at the firing point, so $x_0=y_0=0$. Now, list the known values as follows
(i) Projectile's initial velocity = $800\,{\rm m/s}$
(ii) Angle of projectile: $-30^\circ$, the negative sign is because the throw is below the horizontal.
(iii) y-coordinate of the final point, 150 m below the origin, $y=-150\,{\rm m}$.
In this problem, the time it takes for the cannonball to reach 100 m below the starting point is required.
Since the displacement to that point is known, we apply the vertical displacement projectile formula to find the needed time as below \begin{align*} y-y_0&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\-150&=-\frac 12 (9.8)t^2+(800)\sin(-30^\circ)t\\\\ \Rightarrow & \ 4.9t^2+400t-150=0\end{align*} The above quadratic equation has two solutions, $t_1=0.37\,{\rm s}$ and $t_2=-82\,{\rm s}$. It is obvious that the second time is not acceptable.
Therefore, the cannonball takes 0.37 seconds to reach 150 meters below the firing point.
Problem (6): Someone throws a stone into the air from ground level. The horizontal component of velocity is 25 m/s and it takes 3 seconds for the stone to come back to the same height as before. Find
(a) The range of the stone.
(b) The initial vertical component of velocity
(c) The angle of projection.
Solution: The known values are
(i) The initial horizontal component of velocity, $v_{0x}=25\,{\rm m/s}$.
(ii) The time between the initial and final points, which are at the same level, $t=3\,{\rm s}$.
(a) The range of projectile motion is defined as the horizontal distance between the launch point and impact at the same elevation.
Because the horizontal motion in projectiles is a motion with constant velocity, the distance traveled in this direction is obtained as $x=v_{0x}t$, where $v_{0x}$ is the initial component of the velocity.
If you put the total time the projectile is in the air into this formula, you get the range of the projectile.
In this problem, the stone is thrown from the ground level and, after 3 seconds, reaches the same height. Thus, this is the total time of the projectile.
Hence, the range of the stone is found as below \begin{align*} x&=v_{0x}t\\&=(25)(3)\\&=75\,{\rm m}\end{align*}
(b) The initial vertical component of the projectile's velocity appears in two equations, $v_y=v_{0y}-gt$ and $y-y_0=-\frac 12 gt^2+v_{0y}t$.
Using the second formula is more straightforward because the stone reaches the same height, so its vertical displacement between the initial and final points is zero, i.e., $y-y_0=0$. Setting this into the vertical distance projectile equation, we get \begin{align*} y-y_0&=-\frac 12 gt^2+v_{0y}t\\\\ 0&=-\frac 12 (9.8)(3)^2+v_{0y}(3) \\\\ \Rightarrow v_{0y}&=14.7\quad{\rm m/s}\end{align*} To use the first formula, we need some extra facts about projectile motion in the absence of air resistance, as below
(i) The vertical velocity is zero at the highest point of the path of the projectile, i.e., $v_y=0$.
(ii) If the projectile lands at the same elevation from which it was launched, then the time it takes to reach the highest point of the trajectory is half the total time between the initial and final points.
The second note, in the absence of air resistance, is only valid.
In this problem, the total flight time is 3 s because air resistance is negligible, so 1.5 seconds are needed for the stone to reach the maximum height of its path.
Therefore, using the second equation, we can find $v_{0y}$ as below \begin{align*} v_y&=v_{0y}-gt\\0&=v_{0y}-(9.8)(1.5) \\\Rightarrow v_{0y}&=14.7\quad {\rm m/s}\end{align*}
(c) The projection angle is the angle at which the projectile is thrown into the air and performs a two-dimensional motion.
Once the components of the initial velocity are available, using trigonometry, we can find the angle of projection as below \begin{align*} \theta&=\tan^{-1}\left(\frac{v_{0y}}{v_{0x}}\right)\\\\&=\tan^{-1}\left(\frac{14.7}{25}\right)\\\\&=+30.45^\circ\end{align*} Therefore, the stone is thrown into the air at an angle of about $30^\circ$ above the horizontal.
Problem (7): A ball is thrown at an angle of 60° with an initial speed of 200 m/s. (Neglect the air resistance.)
(a) How long is the ball in the air?
(b) Find the maximum horizontal distance traveled by the ball.
(c) What is the maximum height reached by the ball?
Solution: We choose the origin to be the ball's initial position so that $x_0=y_0=0$. The given data is
(i) The projection angle: $60^\circ$.
(ii) Initial speed : $v_0=200\,{\rm m/s}$.
(a) The initial and final points of the ball are at the same level, i.e., $y-y_0=0$.
Thus, the total time the ball is in the air is found by setting $y=0$ in the projectile equation $y=-\frac 12 gt^2+v_{0y}t$ and solving for time $t$ as below \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\0&=-\frac 12 (9.8)t^2+(200)(\sin 60^\circ)t\\\\\Rightarrow \quad & \boxed{(-4.9t+100\sqrt{3})t=0} \end{align*} The above expression has two solutions for $t$. One is the initial time, $t_1=0$, and the other is computed as $t_2=35.4\,{\rm s}$.
Hence, the ball has been in the air for about 35 s.
(b) The horizontal distance is called the range of the projectile. By inserting the above time (total flight time) into the horizontal distance projectile equation $x=v_{0x}t$, we can find the desired distance traveled. \begin{align*} x&=(v_0\cos\theta)t\\&=(200)(\cos 60^\circ)(35.4)\\&=3540 \quad {\rm m}\end{align*} Therefore, the ball hits the ground 3540 meters away from the throwing point.
(c) Using the projectile equation $v_y^2-v_{0y}^2=-2g(y-y_0)$, setting $v_y=0$ at the highest point of the path, and solving for the vertical distance $y$, the maximum height is found as follows \begin{align*} v_y^2-v_{0y}^2&=-2g(y-y_0)\\0-(200\sin 60^\circ)^2&=-2(9.8)y\\\Rightarrow y&=1531\quad {\rm m}\end{align*} Another method: As mentioned above, the ball hits the ground at the same level as before, so by knowing the total flight time and halving it, we can find the time it takes the ball to reach the highest point of its trajectory.
Therefore, by setting the half of the total flight time in the following projectile kinematic formula and solving for $y$, we can find the maximum height as \begin{align*} y-y_0&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\y&=-\frac 12 (9.8)(17.7)^2+(200\sin60^\circ)(17.7)\\\\&=1531\quad {\rm m}\end{align*} Hence, the ball reaches 1531 meters above the launch point.
Problem (8): What are the horizontal range and maximum height of a bullet fired with a speed of 20 m/s at 30° above the horizontal?
Solution: first, find the total flight time, then insert it into the horizontal displacement projectile equation $x=v_{0x}t$ to find the range of the bullet.
Because the bullet lands at the same level as the original, its vertical displacement is zero, $y-y_0=0$, in the following projectile formula we can find the total flight time \begin{align*} y-y_0&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\0&=-\frac 12 (9.8)t^2+(20)(\sin30^\circ)t\\\\ \Rightarrow & (-4.9t+10)t=0\end{align*} Solving for time $t$ gives two solutions: one is the initial time $t_1=0$, and the other is $t_2=1.02\,{\rm s}$. Thus the total time of flight is 2.04 s.
Therefore, the maximum horizontal distance traveled by the bullet, which is defined as the range of the projectile, is calculated as \begin{align*} x&=(v_0\cos\theta)t\\&=(20\cos 30^\circ)(2.04)\\&=35.3\quad {\rm m}\end{align*} Hence, the bullet lands about 17 m away from the launch point.
Because the air resistance is negligible and the bullet lands at the same height as the original, the time it takes to reach the highest point of its path is always half the total flight time.
On the other hand, recall that the vertical component of velocity at the maximum height is always zero, i.e., $v_y=0$. By inserting these two notes into the following projectile equation, we have \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\&=-\frac 12 (9.8)(1.02)^2+(20\sin 30^\circ)(1.02)\\\\&=5.1\quad {\rm m}\end{align*} We could also use the kinematic equation $v_y^2-v_{0y}^2=-2g(y-y_0)$, to find the maximum height as below \begin{align*} v_y^2-(v_0 \sin \theta)^2 &=-2g(y-y_0) \\ 0-(20\sin 30^\circ)^2 &=-2(9.8)H\\ \Rightarrow H&= 5.1\quad {\rm m} \end{align*} I think the second method is much simpler.
Problem (9): A projectile is fired horizontally at a speed of 8 m/s from an 80-m-high cliff. Find
(a) The velocity just before the projectile hits the ground.
(b) The angle of impact.
Solution: In this problem, the angle of the projectile is zero because it is fired horizontally.
The velocity at each point of a projectile trajectory (path) is obtained by the following formula: \[v=\sqrt{v_x^2+v_y^2}\] where $v_x$ and $v_y$ are the horizontal and vertical components of the projectile's velocity at any instant of time.
(a) Recall that the horizontal component of the projectile's velocity is always constant and, for this problem, is found as \begin{align*} v_x&=v_0\cos\theta\\&=8\times \cos 0^\circ\\&=8\quad {\rm m/s}\end{align*} To find the vertical component of the projectile velocity at any moment, $v_y=v_0\sin\theta-gt$, we should find the time taken to reach that point.
In this problem, that point is located just before striking the ground, whose coordinates are $y=-80\,{\rm m}, x=?$.
Because it is below the origin, which is assumed to be at the firing point, we inserted a minus sign.
Because displacement in the vertical direction is known, we can use the projectile formula for vertical distance.
By setting $y=-80$ into it and solving for the time $t$ needed the projectile reaches the ground, we get \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t\\\\-80&=-\frac 12 (9.8)t^2+(8\times \sin 0^\circ)t\\\\\Rightarrow t&=\sqrt{\frac{2(80)}{9.8}}\\\\&=2.86\quad {\rm s}\end{align*} Now insert this time into the $y$-component of the projectile's velocity to find $v_y$ just before hitting the ground \begin{align*} v_y&=v_0\sin\theta-gt\\ &=8\sin 0^\circ-(9.8)(2.86)\\&=-28\quad {\rm m/s}\end{align*} Now that both components of the velocity are available, we can compute its magnitude as below \begin{align*} v&=\sqrt{v_x^2+v_y^2}\\\\&=\sqrt{8^2+(-28)^2}\\\\&=29.1\quad {\rm m/s}\end{align*} Therefore, the projectile hits the ground at a speed of 29.1 m/s.
(b) At any instant of time, the velocity of the projectile makes some angle with the horizontal, whose magnitude is obtained as the follows: \[\alpha=\tan^{-1}\left(\frac{v_y}{v_x}\right)\] Substituting the above values into this formula, we get \[\alpha =\tan^{-1}\left(\frac{-28}{8}\right)=-74^\circ\] Therefore, the projectile hits the ground at an angle of 74° below the horizontal.
Problem (10): From a cliff 100 m high, a ball is kicked at $30^\circ$ above the horizontal with a speed of $20\,{\rm m/s}$. How far from the base of the cliff did the ball hit the ground? (Assume $g=10\,{\rm m/s^2}$).
Solution: Again, similar to any projectile motion problem, we first select a coordinate system and then draw the path of the projectile as shown in the figure below,
We choose the origin to be at the kicking point above the cliff, setting $x_0=y_0=0$ in the kinematic equations.
The coordinate of the hitting point to the ground is $y=-100\,{\rm m}, x = ?$. A negative is inserted because the final point is below the origin.
Now, we find the common quantity in projectile motions—that is, the time between the initial and final points, called total flight time.
To find the total time the ball was in the air, we can use the vertical equation and solve for the unknown $t$ as follows \begin{align*} y&=-\frac 12 gt^2 +(v_0\sin \theta)t \\\\ -100&=-\frac 12 (10) t^2+(20\sin 30^\circ)t\\\\&\Rightarrow \quad \boxed{t^2-2t-20=0} \end{align*} The solutions of a quadratic equation $at^2+bt+c=0$ are found by the formula below \[t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] By matching the above constant coefficients with the standard quadratic equation, we can find the total time as below \[t=\frac{-(-2)\pm\sqrt{(-2)^2-4(1)(-20)}}{2(1)}\] After simplifying, two solutions are obtained, $t_1=5.6\,{\rm s}$ and $t_2=-3.6\,{\rm s}$.
It is obvious that time cannot be negative in physics, so the acceptable answer is $t_1$.
It is the time it takes the ball to travel in the vertical direction. On the other hand, it is also the time it takes the ball to travel the horizontal distance between kicking and hitting points.
We insert this time into the horizontal equation to find the horizontal distance traveled, known as the projectile's range. \begin{align*} x&=(v_0\cos \theta)t\\ &=(20)(\cos 30^\circ)(5.6)\\&=97\quad {\rm m}\end{align*}
Problem (11): A cannonball is fired from the top of a $200\,{\rm m}$ cliff with a speed of $60\,{\rm m/s}$ at an angle of $60^\circ$ above the horizontal. Where does the ball land closest to which of the following choices? (Neglect air resistance.)
(a) 90m (b) 402 m (c) 151 m (d) 200 m
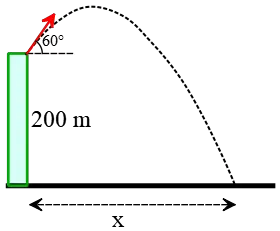
Solution: The horizontal distance from the point where the cannonball fired is wanted, $x=?$. The appropriate kinematic equation for this is \[x=(v_0\cos\theta)t\] The only thing we need is the total time the ball is in the air before landing.
If we take the firing point as the origin, then the cannonball lands $200\,{\rm m}$ below the origin. So, the ball's vertical displacement is $\Delta y=-200\,{\rm m}$. Set this in the vertical displacement equation, $\Delta y=-\frac 12 gt^2+(v_0\sin\theta)t$, and solve for $t$. \begin{gather*} \Delta y=-\frac 12 gt^2 +(v_0\sin\theta)t \\\\ -200=-\frac 12 (10)t^2 +(60\sin 60^\circ)t \\\\ \Rightarrow\quad 5t^2-30\sqrt{3}t-200=0 \\\\ \boxed{t^2-6\sqrt{3}t-40=0}\end{gather*} where we used $\sin 60^\circ=\frac{\sqrt{3}}2$. Using a graphing calculator plot this equation and find its intersections with the horizontal. Consequently, the total flight time is \[\boxed{t=13.4\,{\rm m}}\] Now, substitute this into the horizontal displacement projectile equation below \begin{align*} x&=(v_0\cos\theta)t \\\\ &=(60\,\cos 60^\circ)(13.4) \\\\ &=402\,{\rm m}\end{align*} Thus, the correct answer is (b).
Problem (12): During a kicking drill, a soccer player kicks two successive balls at different angles but with exactly the same speed. The paths that the balls follow are depicted in the figure shown. Which ball remains in the air for a longer time? Neglect air resistance.
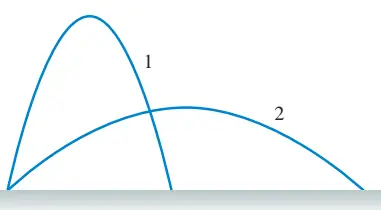
Solution: both balls land at the same level (or the ground), so the total vertical displacement of both is the same, $\Delta y_1=\Delta y_2=0$. The initial kicking speeds are equal $v_{01}=v_{02}$ and as seen from the figure, ball $1$ has greater kicking angle than ball $2$, i.e., $\theta_1>\theta_2$. Setting $\Delta y=0$ in the following equation and solving for $t$, gives us the total time the ball is in the air \begin{gather*} \Delta y=-\frac 12 gt^2+(v_0 \sin\theta)t \\\\ 0=-\frac 12 gt^2+(v_0 \sin\theta)t \\\\ \Rightarrow \boxed{t=\frac{2v_0 \sin\theta}{g}} \end{gather*} Now, substitute the given data into the equation to compare the flight time of both balls \begin{gather*} \theta_1>\theta_2 \\ \sin\theta_1 > \sin\theta_2 \\\\ \frac{2v_0 \sin\theta_1}{g} > \frac{2v_0 \sin\theta_2}{g} \\\\ \Rightarrow \boxed{t_1>t_2} \end{gather*} Thus, ball $1$ will be in the air for a longer time.
Author: Dr. Ali Nemati
Date Published: 6/15/2021
Updated: Jun 22, 2023
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
