Problems and Solutions about displacement and distance are presented which is helpful for high school and college students.
In the following, displacement is computed for simple cases.
Displacement Problems:
Problem (1): An object moves from point A to B, C, and D finally, along a rectangle.
(a) Find the magnitude and direction of the displacement vector of the object?
(b) Find the distance traveled by that object?
(c) Suppose the object returns to point A, its initial position. Now, Find the displacement and distance.
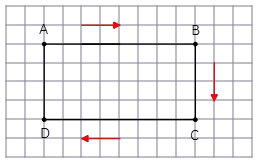
Solution: (a) By definition of displacement, connect the initial (A) and final (D) points together. As shown, displacement is toward the negative of the y-axis and its magnitude is equal to the width of the rectangle. Displacement is used for solving speed and velocity problems
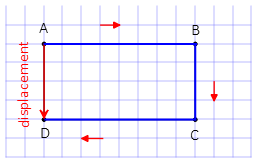
(b) distance is equal to the length of AB+BC+CD.
(c) Since the initial and final positions are the same, so by definition of displacement, the difference between them is zero. But distance, in this case, is the perimeter of the rectangle.
It is also possible to find the displacement of a moving object along a straight line using a position vs. time graph.
Problem 2: An object moves along a right triangle from point A to B to C shown in the figure below. (Consider the sides as $3\,{\rm m}$ and $4\,{\rm m}$)
(a) Find the magnitude and direction of the displacement vector?
(b) How much distance is traveled by this moving object?
(c) Suppose the object returns to point A, its initial position. Now, Find the displacement and distance.
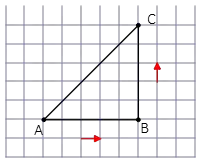
Solution: (a) Connect the initial (A) and final (C) points together by the straightest line. The magnitude and direction of that line represent the displacement vector. Here, the displacement is the hypotenuse of the right triangle. So using the Pythagorean theorem, one finds its magnitude as \begin{align*} c^2 &= a^{2} + b^{2} \\ \Rightarrow c&=\sqrt{a^{2} +b^{2}}\\ &= \sqrt{3^{2} + 4^{2}}=5\,{\rm m} \end{align*} the direction of displacement is shown in figure (to the northeast).
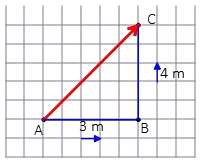
(b) Adding the base and height of this triangle gets the distance traveled from (A) to (C).
\begin{align*} \text{distance} &= a + b\\ &= 3 + 4\\ &= 7\,{\rm m} \end{align*}
(c) Displacement is zero since the object returns to the initial position. Distance is also computed as the perimeter of the triangle.
Problem (3): A kid rides on his bicycle with an average velocity of $12.5\,\rm km/h$ due south in a straight line for 15 minutes. How far has he traveled?
Solution: Recall from average velocity problems that it defines as the displacement divided by the time elapsed, $\bar{v}=\frac{\Delta x}{\Delta t}$. In this displacement problem, the kid does not change its direction of motion and continues moving in the same direction, so its displacement is obtained using the above formula by rearranging it and solving for $\Delta x$. \begin{align*} \Delta x&=\bar{v}t \\ &=(12.5)(\frac 14) \\ &=3.125\,\rm km \end{align*} where in above, we converted $15\,\rm min$ into hours with this fact that every four to $15$ minutes is equal to one hour.
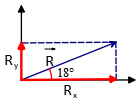
Problem (4): A displacement vector has a magnitude of $810\,{\rm m}$, and points at an angle of $18^\circ$ above the positive x-axis. What are the $x$ and $y$ components of this vector?
Solution: Given the length and direction of a vector such as displacement $\vec{R}$ , one can find its components by the following formulas \begin{align*} R_x &= |\vec{R}|\cos \theta \\ &=(810)\cos 18^\circ=770.35\,{\rm m}\\ \text{And}\\ R_y&=|\vec{R}|\sin \theta \\ &=(810)\sin 18^\circ=250.30\,{\rm m} \end{align*}
Problem (5): A displacement vector is $23\,{\rm km}$ in length and directed $65^\circ$ south of east. What are the components of this vector?
Solution: Like previous problem, displacement in the components form is as $\vec{R}=|\vec{R}|\,\cos \theta \hat{i}+|\vec{R}|\,\sin \theta \hat{j}$ where $\theta$ is measured with the positive $x$-axis. Here, the given angle is below the $x$-axis so we have
\begin{align*} R_x &= |\vec{R}|\cos \theta \\ &=(23)\cos (-65^\circ)=9.72\,{\rm m}\\ \text{And}\\ R_y&=|\vec{R}|\sin \theta \\ &=(23)\sin (-65^\circ)=-20.84\,{\rm m} \end{align*} The minus sign of the y-component indicates the south direction.
Problem (6): A race car will make one lap around a circular track of radius $R$. When the car has traveled halfway around the track, what is the magnitude of displacement of the car from the starting point? Find the distance of the car.
Solution: Displacement is the difference between initial and final points so in this case, that difference is the diameter of the circular track. Thus, \[\text{displacement}=2R\] Distance is also the circumference of the semi-circle that is $2\,\pi R$.
Problem (7): You walk $5\,{\rm km}$ due south then $4\,{\rm km}$ due west. What is the magnitude of your displacement?
Solution: $5\,{\rm km}$ south means a position vector of magnitude $5\,{\rm km}$ from the origin toward the south. The other journey starts from the tail of the previous vector with magnitude and a direction of $4\,{\rm km}$ and west, respectively.
In the mathematical language the above two vectors are written as $\vec{R}_1=5\,(-\hat{j})$ and $\vec{R}_2=4\,(-\hat{i})$. To find the displacement we have two options, either using the drawing vector or the algebraic method which is efficient for more involved problems.
Method I: The vector that is constructed from connecting the tip of the first vector to the tail of the second vector is displacement (triangle method). Recall from the vector practice problems that we used the Pythagorean theorem to get the magnitude of the desired vector.
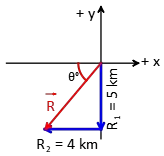
Method II: In the case of several journey segments, displacement can be determined using the methods of vector addition. Here, the whole journey is formed of the two segments with the corresponding vectors $\vec{R}_1=5\,(-\hat{j})$ and $\vec{R}_2=4\,(-\hat{i})$. Thus, using the vector addition method we get \begin{align*} \vec{R}&=\vec{R}_1+\vec{R}_2\\ &=5\,(-\hat{j})+4\,(-\hat{i})\\ \text{or} \ &=-4\,\hat{i}-5\,\hat{j} \end{align*} The magnitude and direction of the above vector is determined by the following formulas \begin{align*} |\vec{R}|&=\sqrt{R_1^2 + R_2^2}\\ &=\sqrt{(-5)^2 + (-4)^2}\\ &=\sqrt{41}\,{\rm km}\\ \text{And}\\ \theta &=\tan^{-1}\left(\frac{R_y}{R_x}\right)\\ &=\tan^{-1}\left(\frac{-5}{-4}\right)\\ &=51.34^\circ \end{align*} Since the $x$ and $y$ components of the displacement place in the third quadrant so the above angle is toward the west south.
Important notes about solving problems on displacement and distance:
- If the initial and final points are the same, so the total displacement is zero.
- Distance is measured as the perimeter of the path traveled by the moving object.
Last Updated: Oct 1, 2022

 kinematic
kinematic
 Electrostatic
Electrostatic
 Magnetism
Magnetism