- Home
- Physics Problems
- Problems
Solved Problems
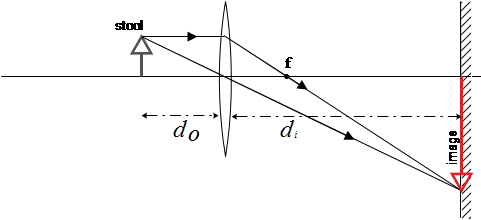
A $0.75\, {\rm m}$ footstool is placed in front of a lens. On a screen $4.00\,{\rm m}$ away from the stool is displayed the stool's image. The image of the stool is $3.00\,{\rm m}$ tall on the screen.
(a) Is the lens used a positive or negative lens? Characterize the image formed on the screen.
(b) Determine $d_i\,\ d_o$ and $f$ for this lens.
(c) Construct a ray-tracing diagram for the situation.
(a) Note: properties of lenses:
- A converging lens has a positive focal length. If $d_o>f$ then the image distance $d_i$ is positive (that is, the image is formed on the other side of the lens, inverted and real). If $d_o<f$ then $d_i<0$ (that is, object and image is located in the same side, virtual and larger)
- A diverging lens has a negative focal length and the object and image are on the same side so $d_i<0$.
This lens has properties of the converging lens due to the larger image and image formed on the other side of the lens, as well. Thus, this is a problem about a converging lens.
(b) The object-image relationship for lens are similar to the spherical mirrors.
\[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\ \ \ {\rm and\ \ }\ M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}\]
In this problem $d_i=L-d_o$ where $L$ is the distance between image and object so
\[\left|-\frac{L-d_o}{d_o}\right|=\frac{h_i}{h_o}=\frac{0.75}{3}=4\ \Rightarrow L-d_o=4d_o\]
\[4-d_o=4d_o\to d_o=0.8{\rm m\ \ and\ \ }{{\rm d}}_{{\rm i}}{\rm =L-}{{\rm d}}_{{\rm o}}==3.2\ {\rm m}\]
\[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\to f=\frac{d_od_i}{d_o+d_i}=\frac{0.8\times 3.2}{3.2+0.8}=0.64\ {\rm m}\]
Note: the object is placed at $f<d_o<2f$, just what is needed for real and inverted image on screen.
(c)
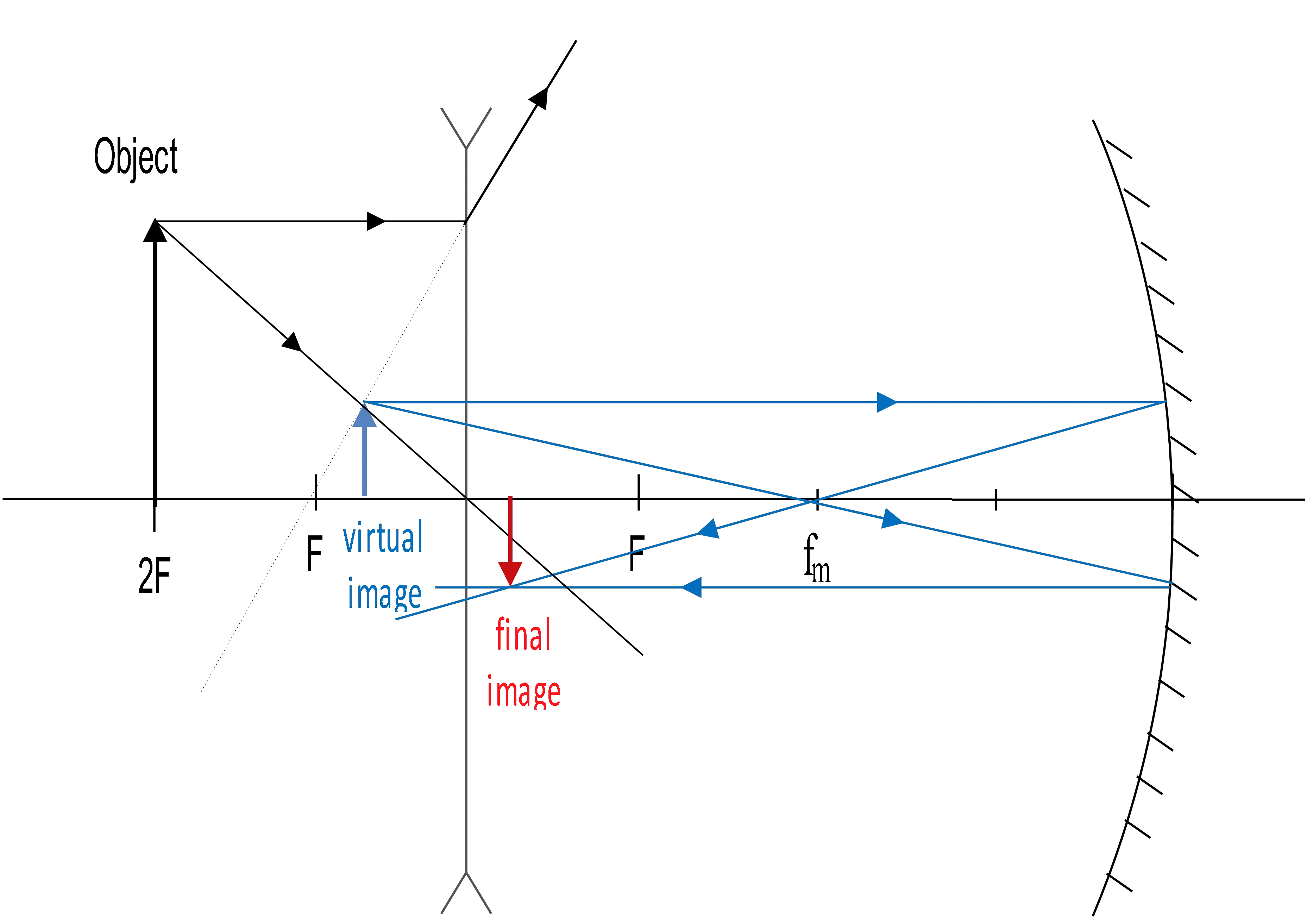
An object is placed $10\, {\rm cm}$ to the left of a diverging lens ($f=-5\,{\rm cm}$). A concave mirror ($R=20\,{\rm cm}$) is placed $20\,{\rm cm}$ to the right of the lens. Calculate the location of the final image with respect to the lens.
First, from the thin lens equation (same as the mirror equation), find the location of the image from lens(figure 1):
\[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\to \frac{1}{d_i}+\frac{1}{10}=\frac{1}{-5}\to d_i=-\frac{10}{3}{\rm cm}=-3.33\ {\rm cm}\]
This virtual image (the minus sign indicates this) acts as the object for the mirror. So find its image distance.
By definition, the focal length of the mirror is: $f_m=\frac{R}{2}=10\,{\rm cm}$ and the distance of the object to it as shown in the figure 2, is $d_{om}=3.33+20=23.33\ {\rm cm}$.
Use the mirror equation to find the image distance
\[\frac{1}{d_{im}}+\frac{1}{d_{om}}=\frac{1}{f_m}\to \ \frac{1}{23.3}+\frac{1}{d_{im}}=\frac{1}{10}\to d_{im}=17.5\ {\rm cm}\]
This is final image formed at $17.5\ {\rm cm}$ to the left of the mirror.
Object $O_1$ is $15\, {\rm cm}$ to the left of a converging lens of $10\, {\rm cm}$ focal length. A second lens is positioned $10\, {\rm cm}$ to the right of the first lens and is observed to form a final image at the position of the original object $O_1$.
(b) What is the focal length of the second lens?
(b) What is the overall magnification of this system?
(c) Is the final image real or virtual, upright or inverted? Justify your answer.
(a) The object distance and focal length of the lens $1$ are given. So use the thin lens equation to determine the image distance of this lens 1:
\[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f_1}\to \frac{1}{d_i}=\frac{1}{10}-\frac{1}{15}=\frac{1}{30}\ \Rightarrow d_i=+30\,{\rm cm\ }\]
Now use again the thin lens equation, to find the focal length of the lens $2$:
\[\frac{1}{d_{i_2}}+\frac{1}{d_{O_2}}=\frac{1}{f_2}\to \ \frac{1}{25}+\frac{1}{30-10}=\frac{1}{f_2}\ \Longrightarrow f_2=+11.1\ {\rm cm}\ \]
Since the focal length is positive, this lens is converging lens.
(b) Overall magnification is defined as the multiplication of each of the magnification of the lenses. Thus
\[M_{tot}=m_1m_2=\left(-\frac{d_{i1}}{d_{o1}}\right)\left(-\frac{d_{i_2}}{d_{o_2}}\right)=\left(-\frac{30}{15}\right)\left(-\frac{25}{20}\right)=2.5\ \]
(c) Final image is
(i) Erect since M is positive.
(ii) is positive.

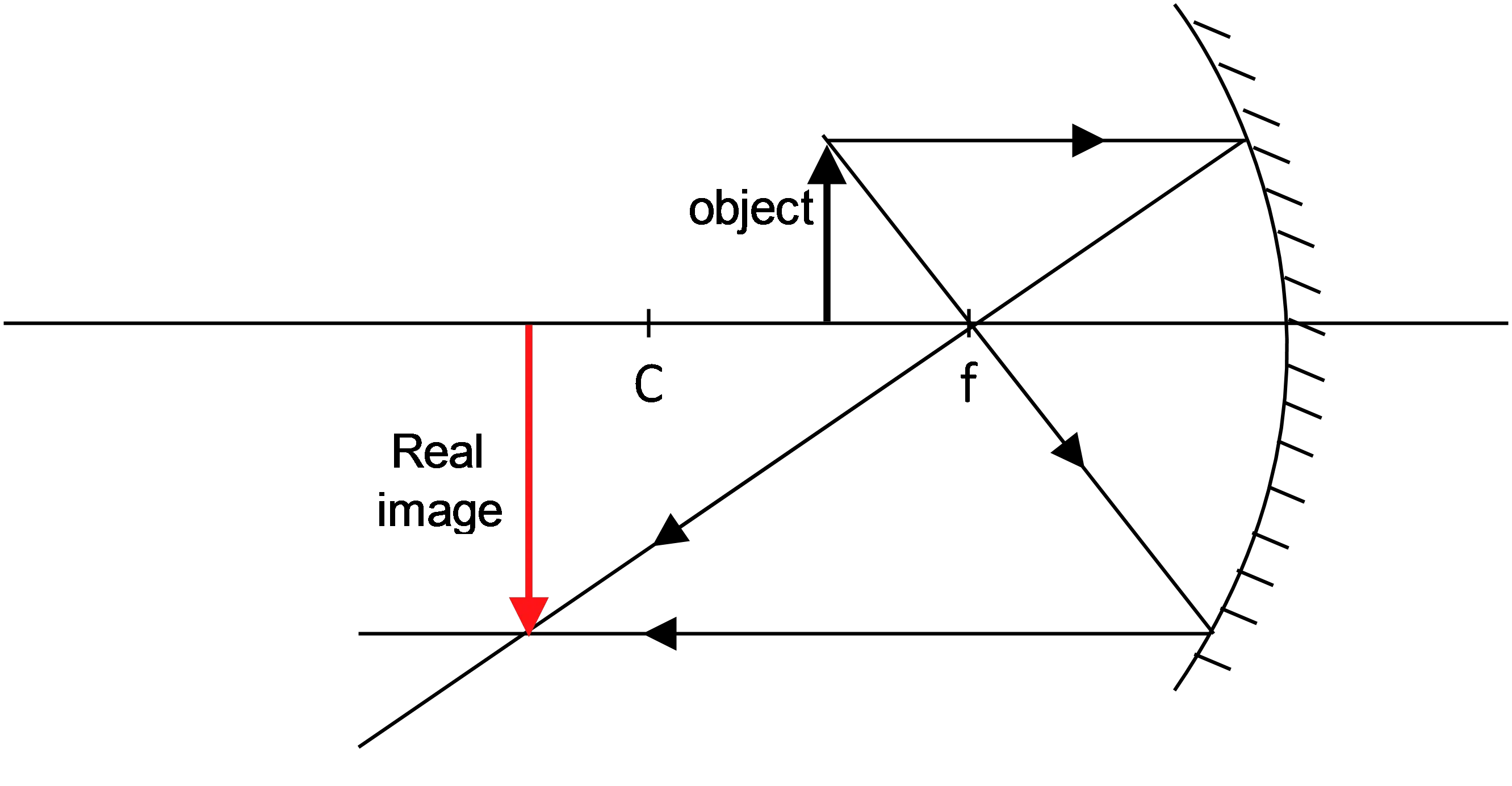
A $10\,{\rm cm}$ tall candle is placed $40\,{\rm cm}$ in front of a concave mirror of radius $R=60\,{\rm cm}$.
(a) Determine the position and size of the image of the candle formed by this mirror.
(b) Characterize this image and draw a ray diagram on the above figure.
(c) A second mirror (convex) whose radius $R=60\,{\rm cm}$ is placed $10\,{\rm cm}$ to the left of the candle. The convex surface is the surface facing the candle. Determine the position and size of the image of the candle formed by the convex mirror.
(d) Determine the position and size of the image of the candle formed by the convex mirror coming from the rays reflected from the concave mirror.
This is a concave mirror problem in which an object stands between the focal point and the center of the mirror.
(a) Use the mirror equation to find the image distance ($f=\frac{R}{2}=30\,{\rm cm}$)
\[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\to \ \ d_i=\frac{fd_o}{d_o-f}=\frac{30\times 40}{40-30}=120{\rm cm}\]
By definition of magnification, we can obtain Size of the image:
\[M=\frac{h_i}{h_0}=-\frac{d_i}{d_o}\Rightarrow \ \ h_i=h_o\left(\frac{d_i}{d_o}\right)=10\left(\frac{120}{40}\right)=30\ {\rm cm\ }\]
(b) In concave mirror $d_i>0$ and $M<0$ denotes the real image and inverted, respectively.
In addition, this image is larger. To draw the ray-tracing diagram of this mirror, we must at least reflect two rays from the mirror. One is parallel to the optical axis reflects through the focal point and the other ray through the focal point reflects parallel to the axis.
(c) $d^{'}_o=10\,{\rm cm}$ and $f^{'}=-\frac{R}{2}=-30\,{\rm cm}$ (in convex mirror $f<0$)
\[\frac{1}{d^{'}_i}+\frac{1}{d^{'}_o}=\frac{1}{f^{'}}\to d^{'}_i=\frac{f^{'}d^{'}_o}{d^{'}_o-f^{'}}=\frac{-30\times 10}{10-\left(-30\right)}=-7.5\ {\rm cm}\]
Use the definition of the magnification to find the image height.
\[h^{'}_i=h_o\left(\frac{d^{'}_i}{d^{'}_o}\right)=10\left(\frac{7.5}{10}\right)=7.5\ {\rm cm}\]
As expected, in the convex mirror image distance must be negative (virtual image) and the height of the image smaller than the object. Ray tracing for a convex mirror:
- A ray travelling parallel to the principal (optical) axis virtually emerges from the virtual focal point of the mirror.
- A ray that aims at the virtual center of the convex mirror is reflected back along its own path

(d) The image of the concave mirror is now the object for the convex mirror i.e. $d^{''}_o=-70\,{\rm cm}$ and $f^{'}=-30\, {\rm cm}$
Note: due to the object is behind the convex mirror so in this case $d_o<0$!
\[\frac{1}{d^{''}_i}+\frac{1}{d^{''}_o}=\frac{1}{f^{'}}\to d^{''}_i=\frac{f^{'}d^{''}_o}{f^{'}-d^{''}_o}=\frac{-30\times -70}{-30-\left(-70\right)}=-52.5\ {\rm cm}\]
\[h^{''}_i=h^{''}_o\left(\frac{d^{''}_i}{d^{''}_o}\right)=30\left(\frac{52.5}{70}\right)=22.5\ {\rm cm}\]
A spherical mirror is used to form an image, five times as tall as an object, on a screen positioned $5.0\,{\rm m}$ from the mirror.
(a) Describe the mirror (convex or concave, radius of curvature and focal length).
(b) Where the mirror should be placed relative to the object?
(a) The given data are $d_i=5\,{\rm m}$ and ${\rm M}=\frac{h_i}{h_o}=\pm 5$ (since we don't know type of the mirror, so we have inserted both signs to incorporate both erected and inverted image)
If $M=-\frac{d_i}{d_o}=5\to d_o=-1\,{\rm m}$ but this case is not possible because the source cannot be behind the mirror and make an image.
If $M=-\frac{d_i}{d_o}=-5\to d_o=1\,{\rm m}$. So use the mirror equation to find the focal length.
\[\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}\ \Rightarrow f=\frac{d_id_o}{d_i+d_o}=\frac{1\times 5}{1+5}=0.83{\rm m}\]
\[R=2f=1.66\,{\rm m}\]
$f$ is positive so the mirror is concave.
(b) $d_o=1\, {\rm m}$ , i.e. $1m$ in front of the mirror (between mirror and screen)
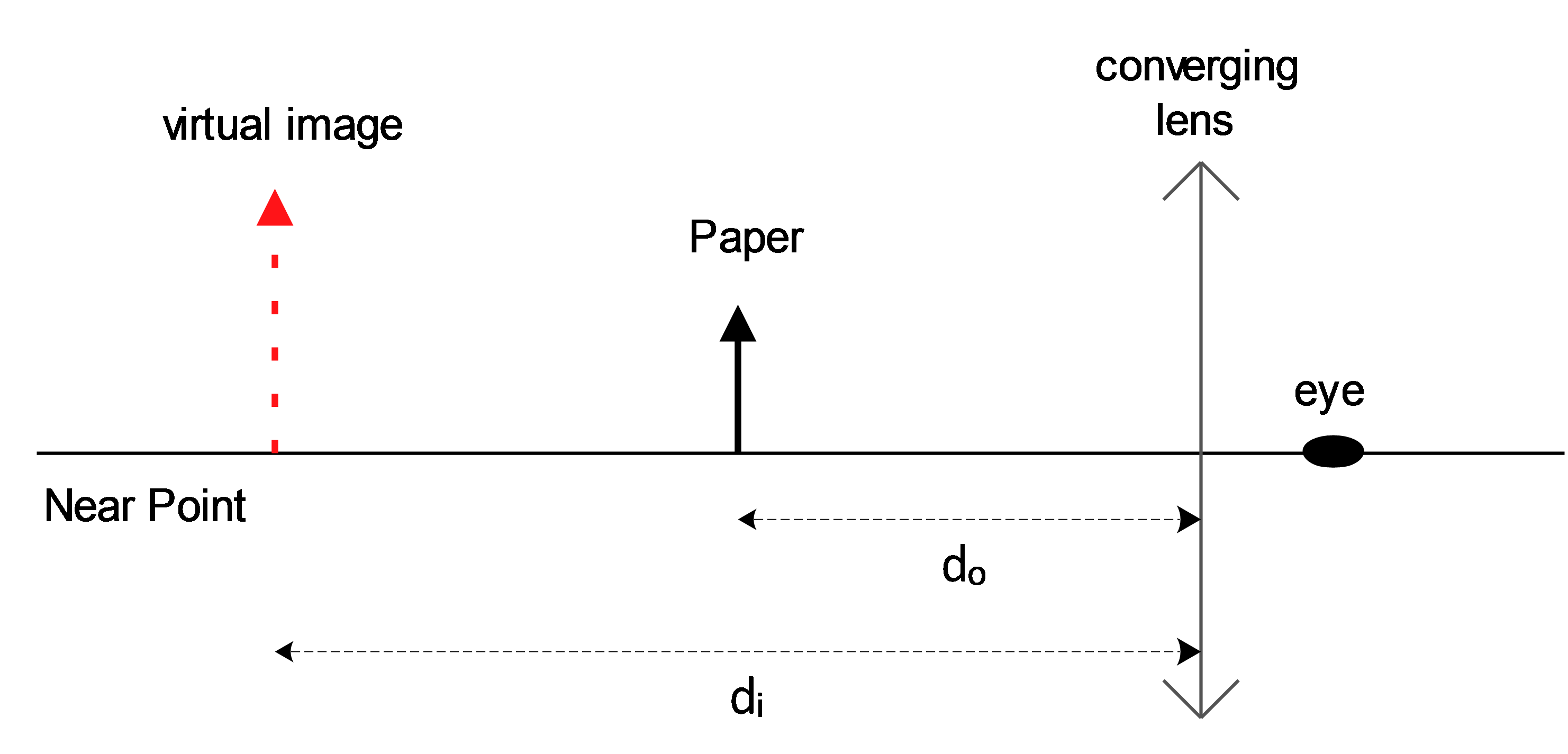
An optometrist prescribes contact lens that have a focal length of $55\,{\rm cm}$.
(a) Are the lenses converging or diverging? Justify your answer.
(b) Is the person wearing the lenses nearsighted or farsighted?
(c) Where is the unaided near point of the person located, if the lenses are designed so that objects no closer than $35\,{\rm cm}$ can be seen clearly?
(a) Converging, because $f$ is positive.
(b) A farsighted person cannot see objects nearer than the near point distance. Whereas the near point of a normal eye is $25\, {\rm cm}$, the near point of a farsighted eye is farther away than that. An image focused behind retina can be focused on the retina by a converging lens. Farsighted people focus near objects behind the retina and need the converging lens.
(c) These lenses create a virtual image from an object located at the near point. In this case near point of the lens-eye system is $35\, {\rm cm}$ that is $d_o=35\, {\rm cm}$. so use the mirror equation and find the virtual image distance $d_i$:
\[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}\ \Rightarrow \frac{1}{55}=\frac{1}{35}+\frac{1}{d_i}\to d_i=-96.25\,{\rm cm}\]
so near point is $96.25\,{\rm cm}$.
A farsighted person has a near point that is $48\,{\rm cm}$ from her eyes. She wears eyeglasses that are designed to enable her to read a newspaper held at a distance of $26\,{\rm cm}$ from her eyes. Find the focal length of the eyeglasses if they are worn $2\,{\rm cm}$ from the eyes.
A farsighted person can see distant objects clearly and farsightedness is corrected with a converging (positive) lens.
Note: For a farsighted person, a sharp image of an object located between the near point and the eye forms behind the retina.
With a converging lens, this image is moved onto the retina. Recall that the image of a first lens acts as the object for a second lens.
In the lens-eye system, the eye is the second lens. The goal is for the person can focus on an object located at a near point (normal vision).
A converging lens forms an upright, virtual image at the person’s actual near point($NP=26 \,{\rm cm}$). This image acts as an object for the eye.
Since after wearing the glasses, she is able to read normally so she has gained normal vision.
In general, normal vision will allow a person to focus on an object $26\,{\rm cm}$ away. The $48\, {\rm cm}$ near point of this person means she can see objects at $48\,{\rm cm}$. using maximum accommodation, we must use a lens that creates a virtual image at position $d_i=-46\,{\rm cm}$ (in lenses if image and object are in the same side then $d_i$ is virtual and negative)from an object at $d_o=24\,{\rm cm}$.
\[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}\ \Rightarrow f=\frac{d_id_o}{d_i+d_o}=\frac{-46\times 24}{-46+24}=+50.2\,{\rm cm}\]
The positive sign indicates that the lens is converging, as expected.
Josh is farsighted and has a near point located $119\,{\rm cm}$ from his eyes. Anne is also farsighted, but her near point is $72\,{\rm cm}$ from her eyes. Both have glasses that correct their visions to a normal near point ($35\,{\rm cm}$ from the eyes), and both wear glasses $3.0\,{\rm cm}$ from the eyes. Relative to the eyes, what is the closet object that can be seen by Josh when he wears Anne's glasses?
First, determine the focal length of Anne's glasses:
Near point of Anne's eyes relative to the glasses is $d_i=72-3=69\,{\rm cm}$ (in this cases $d_i$ should be inserted negative in the relations!). Normal near point considered as object distance, so $d_o=35-3=32\,{\rm cm}$.
\[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\to f=\frac{d_id_o}{d_i+d_o}=\frac{-69\times 32}{-69+32}=+59.67\, {\rm cm}\]
Now if Josh wears the Anne's glasses, we have ($f=59.67\,{\rm cm\ ,\ }d^{'}_i=119-3=116\,{\rm cm}$)
\[d^{'}_o=\frac{d_if}{d_i-f}=\frac{-116\times 59.67}{-116-59.67}=39.4\ {\rm cm}\]
Therefore, when Josh wears the Anne's glasses, this lens creates a virtual image at distance $d^{'}_i=116\ {\rm cm}$ from an object located at $d^{'}_o=39.4+3=42.4\, {\rm cm}$ in front of the Josh's eye. Alternatively, when the objects places at $42.4\, {\rm cm}$ and farther away from the Josh's eye, he can see a focused image on the retina.
Two identical diverging lenses are separated by $18\,{\rm cm}$. The focal length of each lens is $-8.0\,{\rm cm}$. A $6{\rm cm}$ tall object is located $4.0\,{\rm cm}$ to the left of the lens that is on the left. Clearly label all images.
(a) Construct the ray diagram.
(b) Determine the final image distance relative to the lens on the right.
(c) How tall is the final image?
(a) The ray diagram for this diverging lens problem is shown.
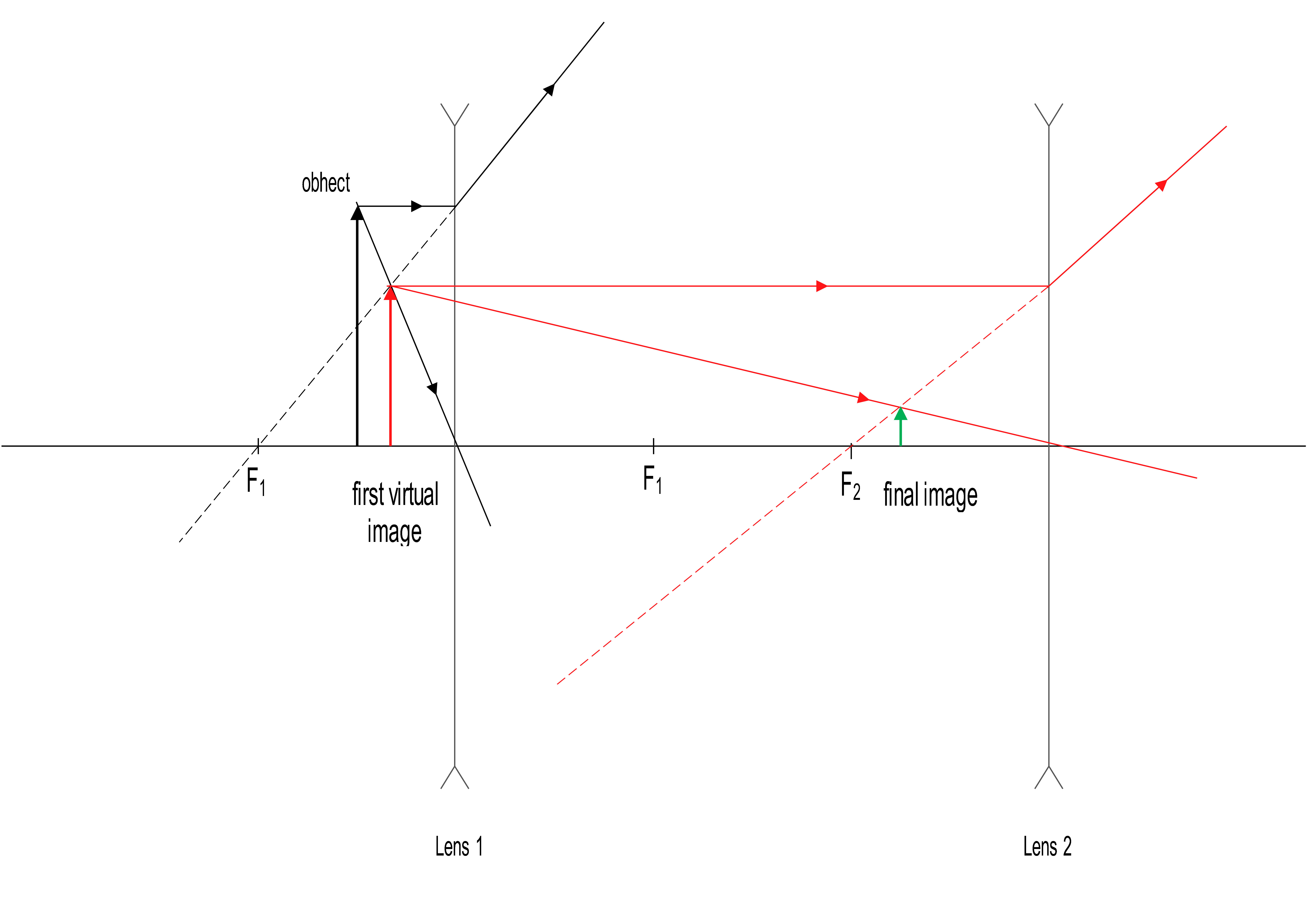
(b) The image of the first lens serves as object for the second lens.
\[\frac{1}{f_1}=\frac{1}{d_{i1}}+\frac{1}{d_{o1}}\to \ \ d_{i1}=\frac{fd_{o1}}{d_{o1}-f}=\frac{-8\times 4}{4-\left(-8\right)}=-2.66\,{\rm cm}\]
Minus sign indicating the virtual image (as we expected). Therefore, distance from the second lens is $d_{o2}=L+\left|d_{i1}\right|=18+2.66=20.66\,{\rm cm}$. Now use again the mirror equation and find the final image distance.
\[\Rightarrow d_{i_2}=\frac{fd_{o_2}}{d_{o_2}-f}=\frac{-8\times 20.66}{20.66-\left(-8\right)}=-5.77\,{\rm cm}\]
(c) Total magnification is defined by
\[M_{tot}=M_1M_2=\left(-\frac{d_{i_1}}{d_{o_1}}\right)\left(-\frac{d_{i_2}}{d_{o_2}}\right)=\frac{2.66\times 5.77}{4\times 20.66}=0.186\]
\[\therefore h_{i_f}=M_{tot}h_{o_f}=0.186\times 6=1.11\ {\rm cm}\]
A candle is placed $12\,{\rm cm}$ in front of a convex mirror. When the convex mirror is replaced with a plane mirror, the image moves $8.5\,{\rm cm}$ farther away from the mirror. Find the focal length of the convex mirror.
Plane mirror has exact reflection i.e. $d_i=-d_o$. Let $d_i$ and $d_{i_2}$as the image distances of convex and plane mirrors, respectively. So as shown in the figure, we have
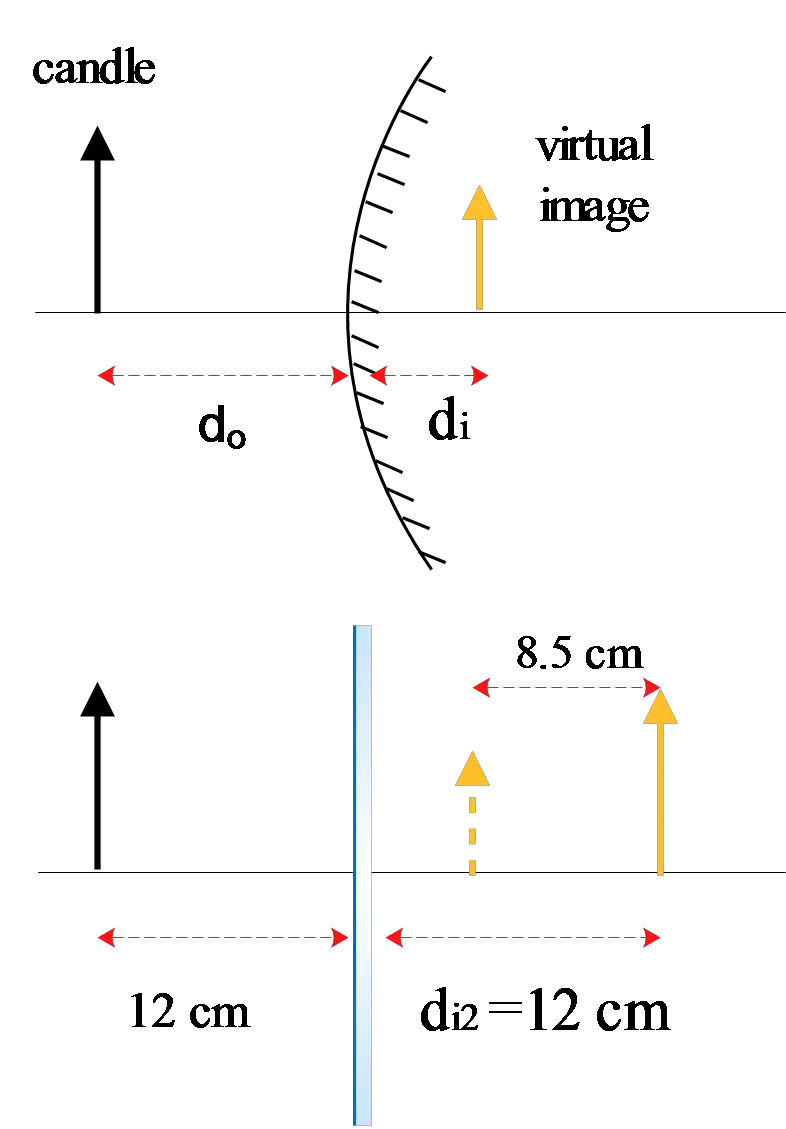
\[d_{i_2}-d_i=8.5\,{\rm cm}\to {{\rm d}}_{{\rm i}}=12-8.5=3.5\,{\rm cm}\]
Use the mirror equation to find the focal length of the convex mirror. Note that the image distance in the convex mirror is negative since image is virtual!
\[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{-3.5}+\frac{1}{12}\ \Longrightarrow f=-4.94\,{\rm cm}\]
Two identical converging lenses with $f=30\,{\rm cm}$ are $70\,{\rm cm}$ apart. A $12\,{\rm cm}$ tall object is placed $100\,{\rm cm}$ in front of the first lens. What is the final height of the object (including sign)?
First, by using thin-lens equation, calculate the image distance of the lens 1
\[\frac{1}{f}=\frac{1}{d_{o_1}}+\frac{1}{d_{i_1}}\to d_{i_1}=42.857\ {\rm cm}\]
\[d_{o_2}=L-d_{o_1}=70-42.857=27.143\ {\rm cm}\]
Now the image of the lens 1 serves as the object for the lens 2. So use again the thin-lens equation and find the final image distance as follows:
\[\frac{1}{f}=\frac{1}{d_{i_2}}+\frac{1}{d_{o_2}}\to d_{i_2}=\frac{fd_{o_2}}{d_{o_2}-f}=\frac{30\times 27.143}{27.143-30}=-285.01\,{\rm cm}\]
The image distance is negative, indicating that the image is virtual and located to the left of the second lens.
The total magnification of the combined optical systems is defined by
\[M_{tot}=M_1M_2=\left(-\frac{d_{i_1}}{d_{o_1}}\right)\left(-\frac{d_{i_2}}{d_{o_2}}\right)=\left(\frac{42.857}{100}\right)\left(-\frac{285.01}{27.143}\right)=-4.5\]
\[M_{tot}=\frac{H_f\left(final\ height\right)}{H_i(initial\ height)}\ \Rightarrow H_f=H_iM_{tot}=12\times \left(-4.5\right)=-54\ {\rm cm}\ \]
Negative indicates that the final image is inverted.
An object is located $14\,{\rm cm}$ in front of a concave mirror, with the image $7\,{\rm cm}$ in front of the mirror. A second object, one third as tall as the first one, is placed in front of the mirror, but at a different location. The image of this second object has the same height (in magnitude only) as the first image, but the orientation is flipped. How far in front of the mirror, is the second object located?
First, use the mirror equation to find the focal length of the mirror:
\[\frac{1}{f}=\frac{1}{d_{i_1}}+\frac{1}{d_{o_1}}=\frac{1}{7}+\frac{1}{14}\to f=\frac{14}{3}\,{\rm cm}\]
Using the definition of the magnification, we obtain
\[m_1=-\frac{d_{i_1}}{d_{o_1}}=-\frac{7}{14}=-\frac{1}{2}\ \ ,\ inverted\ image\]
Let $h_{i_1}=h_{i_2}\ $and $h_{o_2}=\frac{1}{3}h_{o_1}$, now use again the definition of the magnification to determine the magnification of the second object in terms of $m_1$
\[m_2=-\frac{d_{i_2}}{d_{o_2}}=\frac{h_{i_2}}{h_{o_2}}=\frac{h_{i_1}}{\left(\frac{1}{3}\right)h_{o_1}}=3m_1=-\frac{3}{2}\]
The first definition of the magnification, gives the image distance of the second object:
\[\Rightarrow m_2=-\frac{d_{i_2}}{d_{o_2}}=-\frac{3}{2}\to d_{i_2}=\frac{3}{2}d_{o_2}\]
Using the relation above and knowing the focal length of the mirror, we can find the object distance of the second object as follows
\[\left\{ \begin{array}{lcl} \frac{1}{f} & = &\frac{1}{d_{i_2}}+\frac{1}{d_{o_2}}=\frac{1}{\left(\frac{3}{2}\right)d_{o_2}}+\frac{1}{d_{o_2}}=\frac{5}{3d_{o_2}} \\ f & = &\frac{14}{3} \end{array}\right.\ \Rightarrow \ f=\frac{3d_{o_2}}{5}\]
\[\therefore \ d_{o_2}=\frac{5}{3}\left(\frac{14}{3}\right)=\frac{70}{9}\ {\rm cm}\]
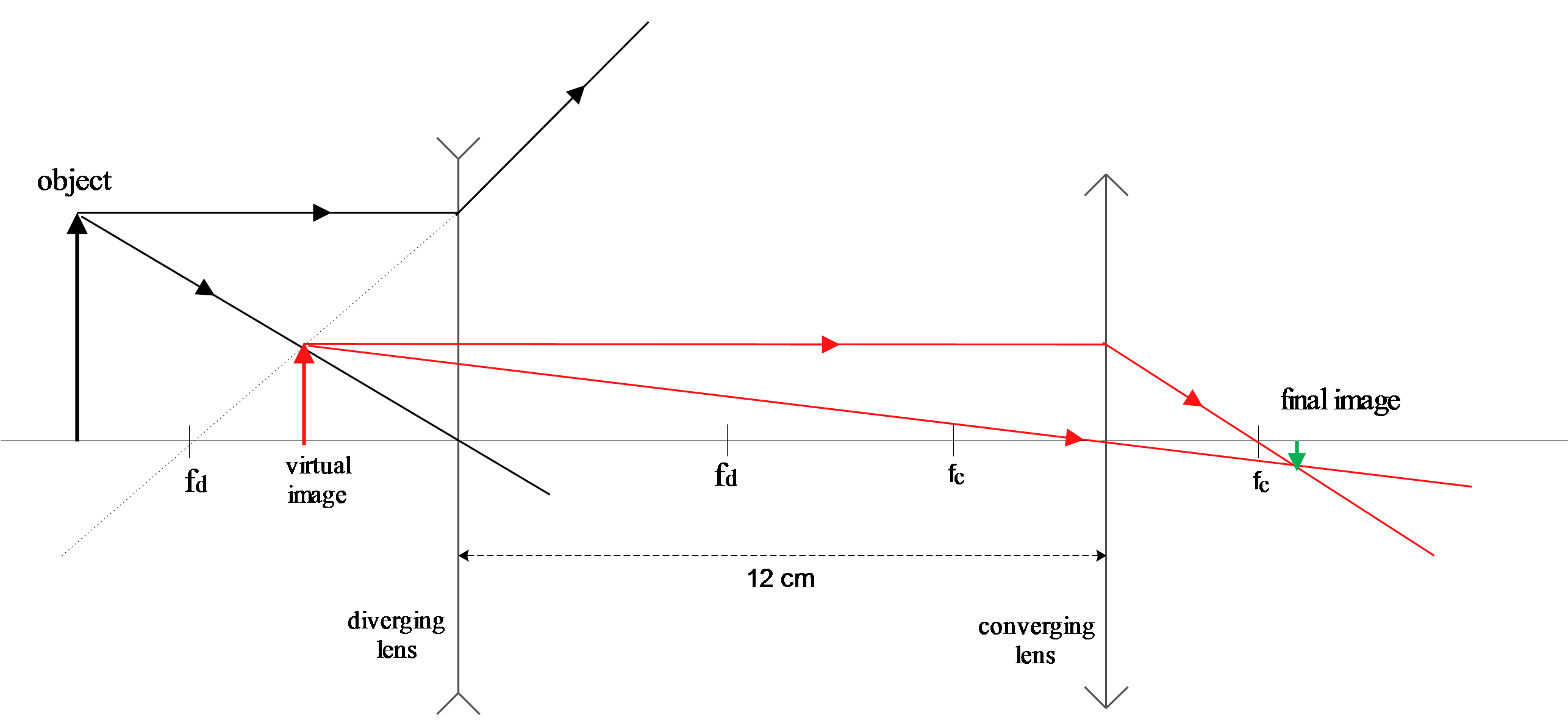
An object is standing to the left of a diverging lens ($f=-8\, {\rm cm}$). A converging lens ($f=6.3\,{\rm cm}$) is $21\,{\rm cm}$ to the right of the diverging lens. The image created by the diverging lens is a distance of $5\,{\rm cm}$ from the diverging lens.
(a) How far is the final image from the object?
(b) What is the height of the final image if the object is $2.0\,{\rm cm}$ tall?
(c) Is the final image virtual or real?
(d) Is the final image inverted or upright?
(a) This is a diverging lens problem so use the lens-thin equation to determine the object distance of the diverging lens
\[\frac{1}{f_d}=\frac{1}{d_i}+\frac{1}{d_o}\to d_o=\frac{f_dd_i}{d_i-f}=\frac{-8\times \left(-5\right)}{-5-\left(-8\right)}=\frac{40}{3}=13.3\ {\rm cm}\]
Note: image in the diverging lens is virtual i.e. $d_i=-5\, {\rm cm}$ and forms in the same side of the object. Now this image serves as the object for the converging lens and its object distance is located at $d^{'}_o=21+5=26\, {\rm cm}$ from the converging lens. so
\[\frac{1}{f_c}=\frac{1}{d^{'}_i}+\frac{1}{d^{'}_o}\to d^{'}_i=\frac{f_cd^{'}_o}{d^{'}_o-f_c}=\frac{6.3\times 26}{26-6.3}=8.31\ {\rm cm}\]
The final image is located at the following distance from the true object.
\[d=d_o+21+d^{'}_i=42.6\ {\rm cm}\]
(b) First, find each of the magnifications and then multiply them together to get the total magnification of combined lenses.
\[m^{'}=-\frac{d^{'}_i}{d^{'}_o}=-\left(\frac{8.31}{26}\right)=-0.31\]
\[m=-\frac{d_i}{d_o}=-\left(\frac{-5}{13.3}\right)=0.37\]
\[M_{tot}=m_1m_2=\frac{H_i}{H_o}\to H_i=2\left(0.37\times \left(-0.31\right)\right)=-0.2294\ {\rm cm}\]
(c) By definition of the magnification, that is $M_{tot}=-D_i/D_o$, we observe that $D_i>0$ then the final image is real.
(d) Because $M_{tot}<0\ $then the final image is inverted
An object sits to the left of a lens at a distance of $74.2\, {\rm cm}$. An inverted image is formed on the right of the lens that is $2.88$ times the size of the object.
(a) Where is the image formed with respect to the lens and is it real or virtual?
(b) What is the focal length of the lens and is this a diverging or converging lens?
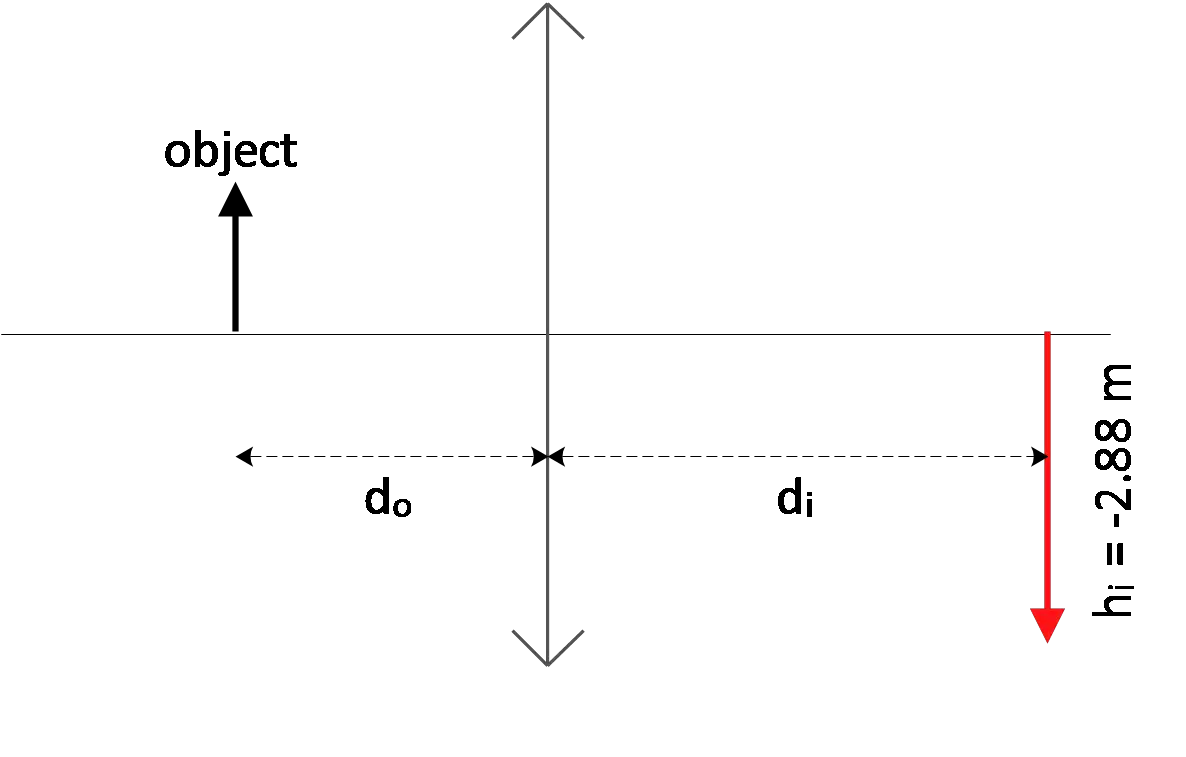
(a) The magnification in the lenses is defined by $M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}$, where $h_i$ and $h_o$are the heights of the image and object, respectively.
Given data: $d_o=74.2\, {\rm cm\ ,\ }h_i=-2.88h_o$. (The negative inserted since the image is inverted). From the magnification equations, we have:
\[-\frac{d_i}{d_o}=\frac{h_i}{h_o}\Rightarrow d_i=-d_o\frac{h_i}{h_o}=-74.2\ \left(\frac{-2.88h_i}{h_i}\right)=213.696\ {\rm cm\ \sim +}214\, {\rm cm}\]
In lenses if the image and object are in the same side then $d_i<0\ $and the image is virtual otherwise is real. Since $d_i>0$ so the image is real.
(b) Use the mirror equation to find the focal length
\[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}\Rightarrow \frac{1}{f}=\frac{1}{214}+\frac{1}{74.2}=0.0181\Rightarrow f=55.09\, {\rm m}\]
Since $f>0$ the lens is converging.
For an object of height $9.00\,{\rm cm}$ located at a distance $1.1\,{\rm m}$ from a mirror, find the height of the image and its distance to the mirror for each of following three cases. In each case also state whether the image is in front or behind the mirror and whether the image is upright or inverted.
(a) Convex mirror with radius of curvature of $R=1.6\,{\rm m}$
(b) Concave mirror with radius of curvature of $R=1.6\,{\rm m}$
(c) Plane mirror.
(a) Use the mirror equation as $\frac{1}{f}=\frac{1}{p}+\frac{1}{q}$ ,where $p$ and $q$ are the distances of object and image from mirror respectively, to find the image distance.
Note: in convex mirrors focal length is negative so $f=-\frac{R}{2}=-0.8\,{\rm m}$ ,
\[\Longrightarrow \frac{1}{-0.8}=\frac{1}{1.1}+\frac{1}{q}\to q=-\frac{0.8\times 1.1}{0.8+1.1}=-0.463\,{\rm m}\]
Since $q<0\ $ then image is virtual. In this mirror image is always located behind the mirror (virtual).
(b) Note: In concave mirror, focal length is positive.($f=+\frac{R}{2}=+0.8\, {\rm m}$)
\[\Rightarrow \frac{1}{f}=\frac{1}{p}+\frac{1}{q}\to q=\frac{fp}{p-f}=-\frac{0.8\times 1.1}{1.1-0.8}=2.93{\rm m}\]
Note: In concave mirrors, depend on the location of the object, both virtual (minus) and real (positive) images can appears.
In above $q>0$ so image is real and located in front of the mirror.
We also specify whether the image is upright or inverted by seeing the sign of the magnification $M=-q/p$ as follows:
In (a) $M=-\frac{-0.463}{1.1}=+0.42$. Since $M>0\ $so image is upright.
In (b) $M=-\frac{2.93}{1.1}=2.6$. Since$M<0$ so image is inverted.
(c) Plane mirror have exact reflection $p=-q=1.1\,{\rm m}$ and image forms as virtual that is image creates in the behind of mirror. So in this mirrors always $M=1>0$ and the image is upright.
A single concave spherical mirror is used to create an image of a $5\,{\rm cm}$ tall source that is located at position$x=0\,{\rm cm}$, which is $20\,{\rm cm}$ to the left point C, the center of the mirror, as shown in the figure below. The magnitude of the radius of curvature for the mirror is $10{\rm cm}$.
(a) What is the source distance $s$ from the mirror?
(b) What is the magnitude and sign of the mirror's focal length?
(c) Using three principal rays, show the resulting image?
(d) Calculate the position $x_i$ where the image is formed?
(d) What is the height $h_i$ of the image?
(e) Is the image upright or inverted? Is it real or virtual?

(a) $p=20+10=30\,{\rm cm}$
(b) The focal length is half of the radius of the curvature of the mirror and is negative for convex mirrors. Therefore, $f=\frac{R}{2}=\frac{10}{2}=+5\,{\rm cm}$
(c) All rays parallel to the optical axis, passing through the focal point and all rays through the center of mirror C, reflects back on them.
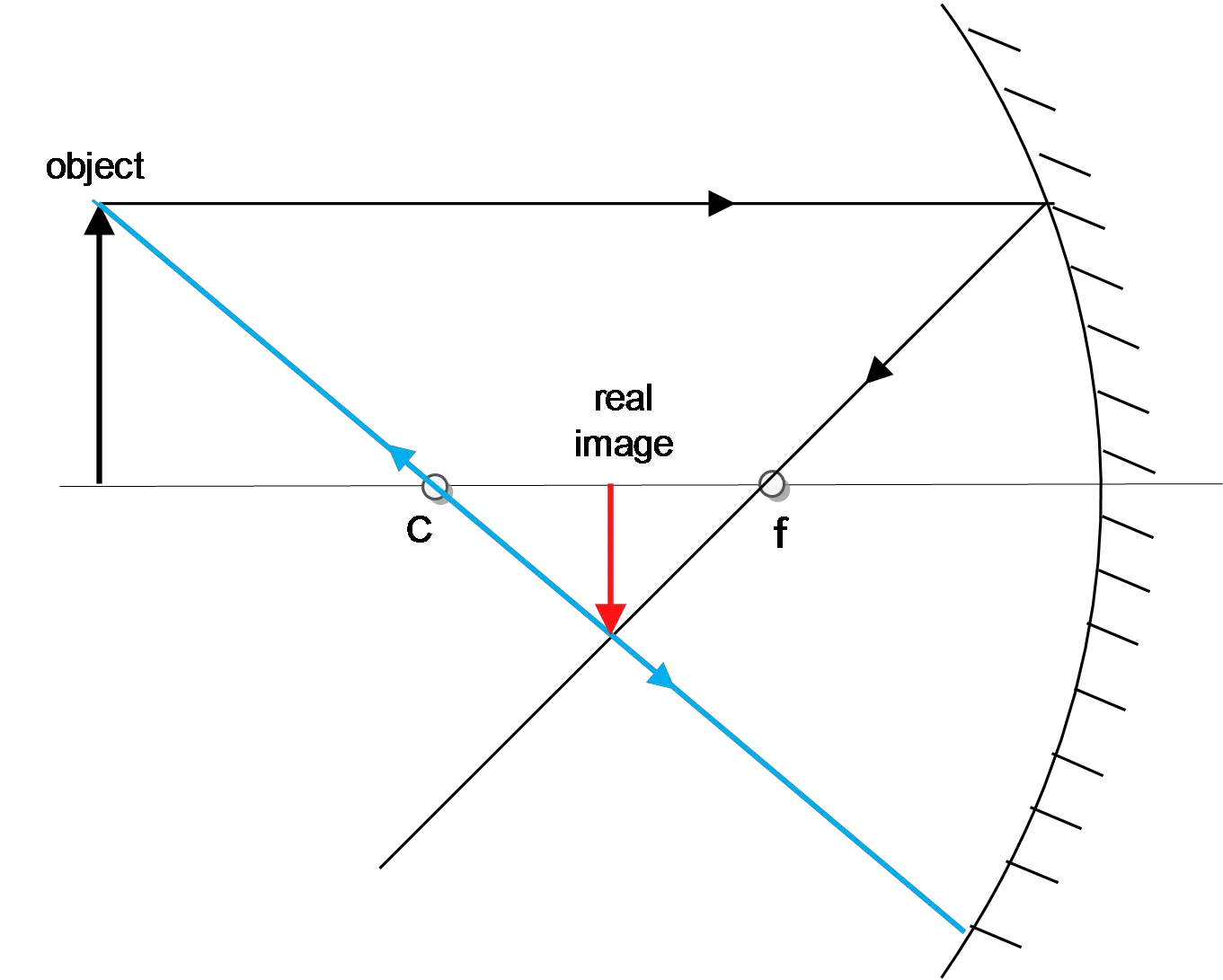
(d) Use the mirror equation as $\frac{1}{f}=\frac{1}{p}+\frac{1}{q}\to q=\frac{fp}{p-f}=\frac{5\times 30}{30-5}=+6\,{\rm cm}$ from the mirror, $x_i=30-6=24\,{\rm cm}$ from $x=0$. Since $q>0$, so the image is real.
(e) Using the magnification equation for a concave mirror problem $M=-\frac{q}{p}=\frac{h_i}{h_o}$, we can find the height of the image.
\[M=-\frac{6}{30}=-0.2\ ,\ \ \ M=\frac{h_i}{h_o}\ \Rightarrow h_i=\left(-0.2\right)\times \ 5=-1\,{\rm cm}\]
The minus sign indicates that the image is inverted!
The image formed by a convex mirror ($R=70\,{\rm cm}$) is located $6\,{\rm cm}$ from the mirror.
(a) What is the image distance?
(b)What is the object distance?
(c) If the height of the image if $4.84\, {\rm cm}$, what is the height of the object?
(d) Characterize the image.
(a) In convex mirror $f<0$ and due to the image is virtual then $d_i<0$ so $f=-\frac{R}{2}=-\frac{70}{2}=-35\,{\rm cm}$ and $d_i=-6\,{\rm cm}$
(b) Use the mirror equation
\[\frac{1}{f}=\frac{1}{d_o}+\frac{1}{d_i}\to d_o=\frac{fd_i}{d_i-f}=\frac{35\times 6}{-6-\left(-35\right)}=7.2\,{\rm cm}\]
(c) Magnification is $M=\frac{h_i}{h_o}=-\frac{d_i}{d_o}\ \Rightarrow h_o=-\frac{d_o}{d_i}h_i=-\left(\frac{7.2}{-6}\right)\left(4.84\right)=5.80\,{\rm cm}\ $
(d) Because $M=-\frac{d_i}{d_o}=-\frac{-6}{7.2}>0\ $ image is erect and since $q<0$ image is virtual (formed on the other side of mirror).
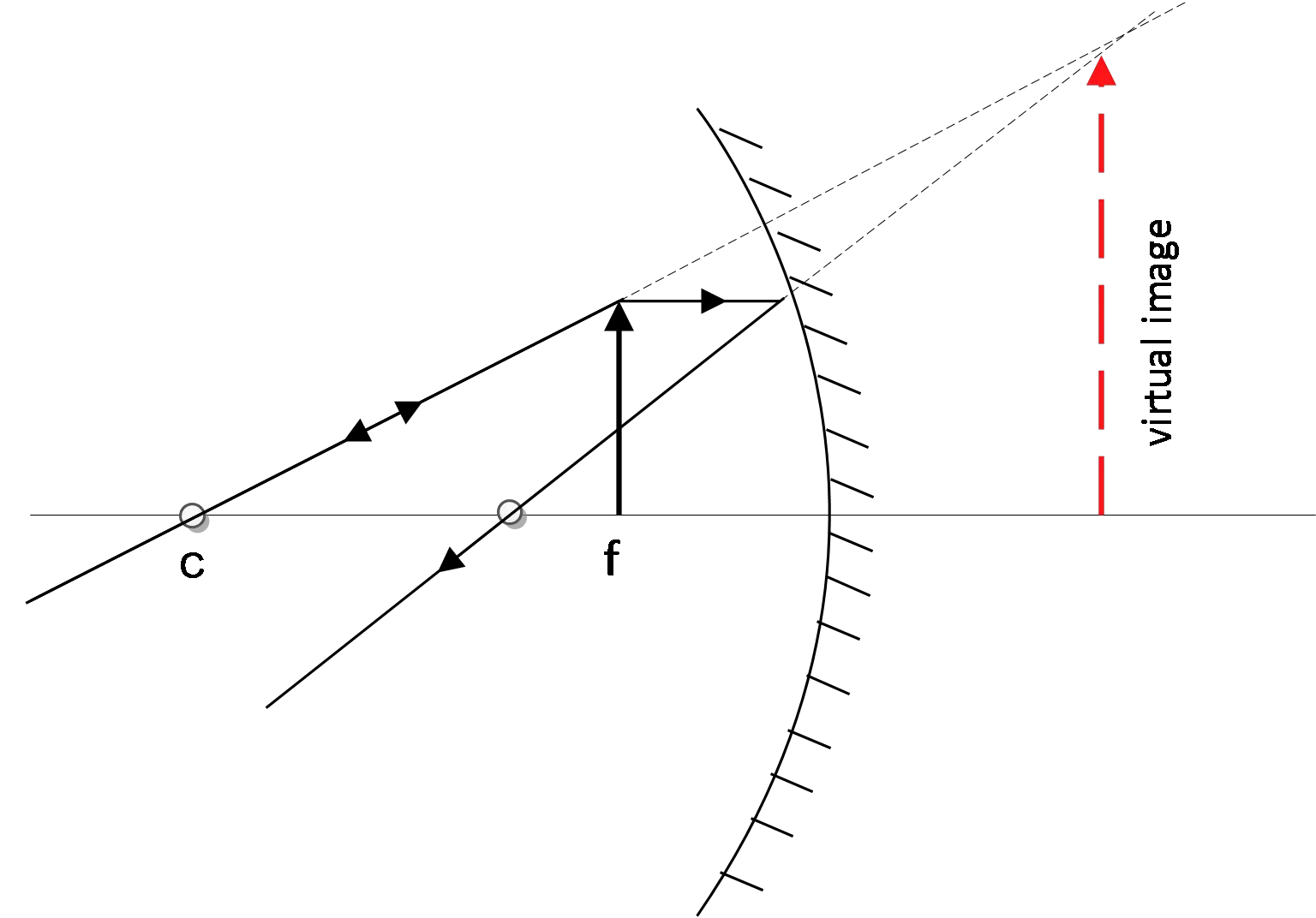
A concave make-up mirror produces an erect image that is $2.5$ times the size of the object when the object is placed $12\,{\rm cm}$ in front of the mirror.
(a) Determine the focal length of the mirror.
(b) Determine the image distance for this setup.
(c) Use an arrow for the object and construct a ray tracing for the situation above.
(a) The given data are: $d_o=12\, {\rm cm\ ,\ M=-}\frac{{{\rm d}}_{{\rm i}}}{d_o}=2.5$. Using the mirror equation, we can find the focal length of the concave mirror
\[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}\to f=\frac{d_id_0}{d_i+d_o}=\frac{-2.5d_o\times d_o}{-2.5d_o+d_o}=\frac{-2.5\times 12}{-1.5}=20\,{\rm cm}\]
(b) Using the magnification equation, we obtain
\[d_i=-Md_o=\left(-2.5\right)\left(12\right)=-30\,{\rm cm}\]
Since $d_i<0$ so the image is virtual.
(c) Apply the principles of the drawing the ray diagrams.
MOST USEFUL FORMULA IN OPTICS:
Lateral magnification in any reflecting or refracting situation:
\[m=\frac{image\ height}{object\ height}=\frac {h_i}{h_o}\]
$m>0 \Longrightarrow$ image is erect.
$m<0 \Longrightarrow$ image is inverted.
Object-Image relationship for mirrors and thin-lenses:
\[\frac 1 s+\frac {1}{s^{'}}=\frac 1 f\]
where $s$ and $s^{'}$ are the object and image distances, respectively.
Focal length and radius of curvature are related as
\[f=\frac R 2\]
© 2015 All rights reserved. by Physexams.com
