- Home
- Physics Problems
- Problems
Solved Problems
Between time $t=0\, {\rm s}$ and $t=8,{\rm s}$, a force ${{\vec{F}=\left(3\hat{i}-4.5\hat{j}\right)\,{\rm N}}}$ moves a $8.3\, {\rm kg}$ object along a trajectory $\Delta \vec{r}=(2.5\hat{i}-2\hat{j}){\rm m}$. How much work is done by this force?
The work done by a constant force $\vec{F}$ over a displacement $\vec{r}$ is $W=\vec{F}.\vec{r}=F\left|r\right|{\cos \theta\ }$ where $\theta$ is the angle between the force and displacement. So
\[W=\vec{F}.\Delta \vec{r}=F_x\Delta x+F_y\Delta y=\left(3\right)\left(2.5\right)+\left(-4.5\right)\left(-2\right)=16.5\, {\rm J}\]
A roller-coaster car moves around a vertical circular loop of radius$R=10.0\,{\rm m}$.
(a) What speed must the car have so that it will just make it over the top without any assistant the track?
(b) What speed will the car subsequently have at the bottom of the loop?
(c) What will be the normal force on a passenger at the bottom of the loop?
At the top, the normal force and gravity are in the same direction. These forces provide the centripetal force $F_r$ acting on the car. If the normal force $N$ becomes zero, then the car is on the verge of falling (but not yet falling). Apply Newton's second law and then set $N=0$. \begin{gather*} \Sigma F_r=ma_r\\\\ N_t+mg=\frac{mv^2_t}{r}\\\\ \Rightarrow\quad mg=\frac{mv^2_t}{r} \end{gather*} Substituting the numerical values into above, we will have \begin{align*}v_t&=\sqrt{Rg} \\ &=\sqrt{10\times 9.8} \\ &=9.9\quad \rm m/s \end{align*}
Use the conservation of mechanical energy between top and bottom points. \begin{gather*} U_{top}=mg(2R) \, , \, K_{top}=\frac{1}{2}mv^2_t \\\\ U_{bot}=0\, ,\, K_{bot}=\frac{1}{2}mv^2_b \\\\ E_{top}=E_{bot} \\\\ \Rightarrow 2mgR+\frac{1}{2}m(gR)=\frac{1}{2}mv^2_b \\\\ \Rightarrow \, \boxed{v_b=\sqrt{5gR}=22.1\,\rm m/s} \end{gather*}
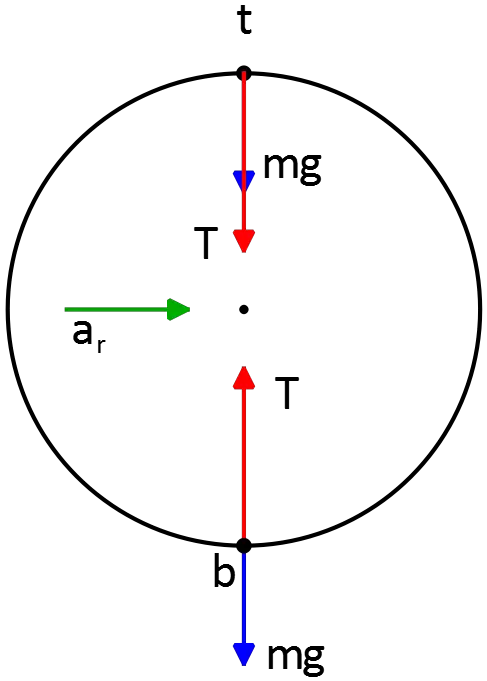
The forces act on the passengers at the bottom are shown in the figure.
Note: in this problems the normal and centripetal forces always are toward the center of the circle i.e. $-\hat{r}$ and the gravity is in outward i.e. $\hat{r}$ direction.\begin{gather*} \Sigma F_r=ma_r \\\\ N(-\hat{r})+mg\hat{r}=\frac{mv^2_b}{r}(-\hat{r}) \\\\ \Rightarrow N_b=mg+\frac{mv^2_b}{r}=mg+\frac{5mgR}{R}=6mg \\\\ \therefore \quad \boxed{N=6mg=14.7\,\rm kN}\end{gather*}
The drag force $F_D$ on the dragster is plotted as a function of distance s below. What is the magnitude of the work done by the drag force after the dragster has traveled $400\, {\rm m}$?
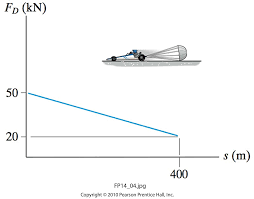
By definition, the area under the force- displacement represents the work done by this force. So $W=\int{\vec {F}.d\vec {x}}$ or $W={\rm area(F-x)}$. Therefore, in this case we must find the area of a trapezoid with lengths of parallel sides $a$ , $b$ and height $h$.

Area of a trapezoid: $A=\frac{a+b}{2}.h$
So the work done by this force is
\[W=\frac{(50{\rm kN}+20{\rm kN)}}{2}\left(400{\rm m}\right)=14\ {\rm MJ}\]
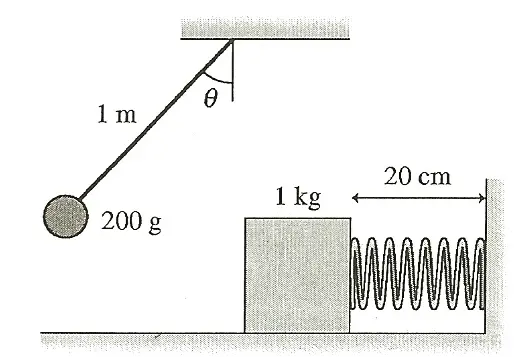
A $200\, {\rm g}$ rubber ball is tied to a $1.0\, {\rm m}$ long string and released from rest at angle $\theta$. It swings down and at the very bottom has a perfectly elastic collision with a $1.0\,{\rm kg}$ block. The block is resting on a frictionless surface and is connected to a $20\,{\rm cm}$ long spring of spring constant $2000\, {\rm N/m}$. After the collision, the spring compresses a maximum distance of $2.0\,{\rm cm}$. from what angle was the rubber ball released?
Conservation of mechanical energy gives the velocity of the ball before the collision: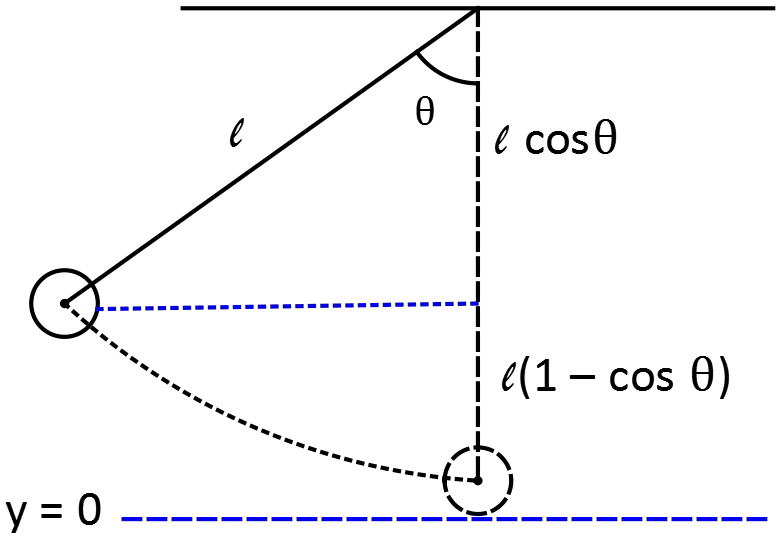
\[E_i=E_f\Rightarrow \ mg\,l\,\left(1-{\cos \theta\ }\right)=\frac{1}{2}mv^2_1\]
$\Rightarrow \ v_1=\sqrt{2gl\,\left(1-{\cos \theta\ }\right)}$
Because of elastic collision, kinetic energy and momentum are conserved.
let $m_1$be the ball and $m_2$ be the block
Use the conservation of momentum $P_i=P_f$ to determine the velocity of the ball and block after the collision:
\[\Rightarrow m_1v_1=m_1v_{1f}+m_2v_2\to v_1=v_f+\frac{m_2}{m_1}v_2\ \ \ \ \ ,\ \ {\rm (I)}\]
Conservation of K.E gives: $\frac{1}{2}m_1v^2_1=\frac{1}{2}m_1v^2_{1f}+\frac{1}{2}m_2v^2_2\to v^2_1=v^2_{1f}+\frac{m_2}{m_1}v^2_2$
From ${\rm (I)}$ we have: $v^2_{1f}=v^2_1-2\frac{m_2}{m_1}v_1v_2+{\left(\frac{m_2}{m_1}v_2\right)}^2$
\[\therefore v^2_1=v_1-2\frac{m_2}{m_1}v_1v_2+{\left(\frac{m_2}{m_1}\right)}^2v^2_2+\frac{m_2}{m_1}v^2_2\]
If the relation above divided by $\frac{m_2}{m_1}v_2$ we obtain:
\[0=-2v_1+\frac{m_2}{m_1}v_2+v_2\ \ \ \Longrightarrow \ \ v_2=\frac{2v_1}{1+\frac{m_2}{m_1}}\]
Now write the conservation of mechanical energy of spring:
\[\frac{1}{2}m_2v^2_2=\frac{1}{2}k{\left(\Delta x\right)}^2\ \ \Longrightarrow v_2=\sqrt{\frac{k}{m}}\Delta x=\sqrt{\frac{2000}{1}}\left(0.2\right)=0.894\frac{{\rm m}}{{\rm s}}\]
by substituting this into above relation for $v_2$ and solve for $v_1$, we obtain
\[v_1=\frac{1}{2}v_2\left(1+\frac{m_2}{m_1}\right)=2.68\frac{{\rm m}}{{\rm s}}\]
\[{\cos \theta\ }=1-\frac{v^2_1}{2gl}\to \theta=50.7{}^\circ \]
A Skier, whose mass is $70\, {\rm kg}$, stands at the top of a $10^\circ$ slope on her new frictionless skis. A strong horizontal wind blows against him with a force of $50\, {\rm N}$. Without using Newton's laws of motion, find the skier's speed after traveling $100\, {\rm m}$ down the slope.
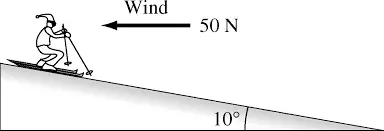
Using the conservation of mechanical energy between the initial and final points, we obtain \begin{gather*} K_i+U_i+W_{wind}=K_f+U_f \\\\ 0+mg(\underbrace{100\,\sin 10^\circ}_{h_i})-50\,{\cos 10^\circ}\times 100=\frac{1}{2}mv^2_f+0 \end{gather*} where $U_i$ is the initial potential energy of the skier. At the top of the slop, its height relative to the ground is $h_i=100\, sin 10^\circ$. $W_{wind}$ is the work done by the force of the wind on the skier. therefore, \begin{gather*} v^2_f=100\left(2g{\sin 10^\circ}-\frac{2\times 50\times {\cos 10^\circ}}{m}\right) \\\\ =100\left(2\times 9.8\times {\sin 10^\circ}-\frac{2\times 50\times {\cos 10^\circ}}{70}\right) \\\\ \Rightarrow\quad \boxed{v_f=14\quad \rm m/s}\end{gather*}
A bullet of mass $m$ and speed $v$ passes completely through a pendulum bob of mass $M$. The bullet emerges with a speed of $v/2$. The pendulum bob is suspended by a stiff rod of length $l$ and negligible mass. What is the minimum value of $v$ such that the pendulum bob will barely swing through a complete vertical circle?
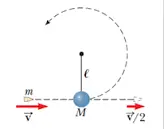
Use the conservation of the momentum to find the velocity of the bullet after the collision.
\[P_i=P_f\to mv=Mv_f+m\frac{v}{2}\ \Rightarrow v_f=\frac{m}{M}\frac{v}{2}\ \ \ (*)\]
Because there is no frictional effects, so mechanical energy of bob is conserved.
\[E_i=E_f\to \ U_i+K_i=U_f+K_f\]
Barely swing through a complete vertical circle means that the bob has some energy to reach only the top of the path. So use the conservation of the mechanical energy between bottom and top point of the circle. Let the lowest point of the pendulum as reference point $U_i(bottom)=0$ and $U_f(top)=Mg(2l)$
\begin{gather*} \frac{1}{2}Mv^2_f=Mg(2l)\to v_f=2\sqrt{gl} \\\\ \text{from} (*) \Rightarrow \boxed{v_{min}=\frac{4M}{m}\sqrt{gl}}\end{gather*}
A block of mass $M$ attached to a horizontal spring with force constant $k$ is moving in SHM with amplitude $A_1$. As the block passes through its equilibrium position, a lump of putty of mass $m$ is dropped from a small height and sticks to it.
(a) Find the new amplitude and period of the motion.
(b) Repeat the first part, find the new amplitude and period of the motion, if the putty is dropped from a small height onto the block, and stick to it when it is at one end of its path.
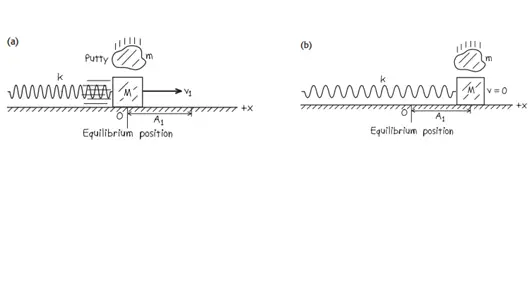
Recall that the total mechanical energy in SHM is $E=\frac{1}{2}mv^2+\frac{1}{2}kx^2=\frac{1}{2}kA^2$.
Where $A$ is the amplitude or maximum distance to the equilibrium. Therefore, before the collision, we have
\[E_1=U_1+K_1=\frac{1}{2}mv^2_1+0\left(in\ equilibrium\ position\right)=\frac{1}{2}kA^2_1\]
\[\Rightarrow v_1=\sqrt{\frac{k}{m}}A_1\]
Conservation of momentum states that $P_i=P_f\ \Rightarrow Mv_1=\left(M+m\right)v_2$
\[\Rightarrow v_2=\frac{M}{M+m}v_1\ \ ,\ after\ collision\]
So the total mechanical energy of the system after the collision is
\[E_2=U_2+K_2\ \Rightarrow \frac{1}{2}kA^2_2=0+\frac{1}{2}\left(m+M\right)v^2_2=\frac{1}{2}\frac{M^2}{M+m}v^2_1\]
\[\Rightarrow E_2=\frac{M}{M+m}E_1\]
\[\Rightarrow \frac{1}{2}kA^2_2=\frac{M}{M+m}\frac{1}{2}kA^2_1\to A_2=\sqrt{\frac{M}{M+m}}A_1\]
In SHM, period is given by $T=2p\sqrt{\frac{m}{k}}$ so $T_f=2p\sqrt{\frac{M_{tot}}{k}}=2p\sqrt{\frac{m+M}{k}}\ \ $
At one ends of a SHM $v=0$ and $E_{tot}=\frac{1}{2}kA^2$ so
\[K_1=K_2=0\ \ ,\ E_{tot,1}=E^{'}_{tot,2}\Rightarrow \ \frac{1}{2}kA_1=\frac{1}{2}kA^{'}_2\ \ \ \]
\[\therefore A_1=A^{'}_2\ {\rm ,\ does\ not\ change!}\]
The period of motion does not change.
Tarzan is in the path of a pack of stampeding elephants when Jane swings in, to the rescue on a rope vine, hauling him off to safety. The length of the vine is $25\,{\rm m}$, and Jane starts her swings with the rope horizontal. If Jane's mass is $54\,{\rm kg}$, and Tarzan's mass is $82\,{\rm kg}$, to what height above the ground will the pair swing after she rescues him?
The collision between Jane and Tarzan is considered a perfectly inelastic collision. We can use conservation of energy to find Jane's speed just before the collision, and then again to find how high they go after the collision.
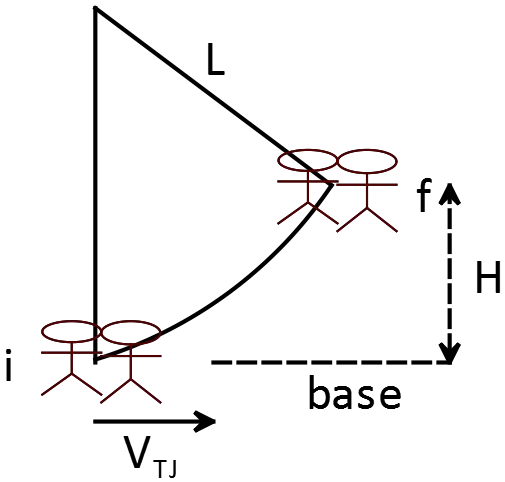
Stage 1: Jane swings
\begin{gather*} E_{i,mech}=U+K=m_{J}gL+0\\ E_{f,mech}=U_f+K_f=0+\frac{1}{2}m_{J}v^2_{J} \end{gather*} Apply conservation of mechanical energy as below \[E_i=E_f\to m_{J}gL=\frac{1}{2}m_{J} v^2_J\Rightarrow v_J={\left(2gL\right)}^{\frac{1}{2}}\]
Stage 2: Jane collide with Tarzan. Use conservation of momentum to find the combined velocity of Tarzan and Jane just after collision:
\begin{gather*} P_i=P_f \\\\ m_Jv_J=\left(m_T+m_J\right)V_{TJ}\\\\ \Rightarrow V_{TZ}=\frac{m_J}{m_J+m_T}v_J\end{gather*} Therefore,\[V_{TJ}=\frac{m_J}{m_J+m_T}{\left(2gL\right)}^{\frac{1}{2}}\]
Stage 3: now use again the conservation of the mechanical energy to determine the desired height:
\begin{gather*}E_i=U_i+K_i=0+\frac{1}{2}\left(m_T+m_J\right)V^2_{TJ}\\\\=\frac{1}{2}\left(m_T+m_J\right){\left(\frac{m_J}{m_J+m_T}\right)}^22gL \\\\E_f=U_f+K_f=\left(m_T+m_J\right)gH+0 \\\\ E_i=E_f\Rightarrow H={\left(\frac{m_T}{m_T+m_J}\right)}^2L={\left(\frac{54}{136}\right)}^225=3.9{\rm m}\end{gather*}
Note that in above $U_i=0$ because in this problem we chose the lowest point of the path as a reference point.
Released from rest at the same height, a thin spherical shell and solid sphere of the same mass $m$ and radius $R$ roll without slipping down an incline through the same vertical drop $H$. Each is moving horizontally as it leaves the ramp. The spherical shell hits the ground at a horizontal distance $L$ from the end of the ramp and the solid sphere hits the ground at a distance of $l'$ from the end of the ramp. Find the ratio $L'/L$.
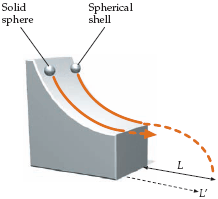
Working backward, if we know the horizontal velocities at the end of the ramp, the distances traveled are $L=V\Delta t$ and $L^{'}=V^{'}\Delta t$ where $\Delta t$ is the time for both to fall vertically from the bottom of the ramp to the ground.
Thus, we conclude $\frac{L}{L'}=\frac{V}{V'}$.
Using the conservation of mechanical energy, we can find $V$ and $V'$. (Let the end of the ramp to be as the reference point i.e. $U=0$)
\begin{gather*} E_i=mgH\\E_f=K_f+U_f=\frac{1}{2}I\omega^2+\frac{1}{2}mV^2\end{gather*}Recall that for a spherical shell, $I=\frac{2}{3}mR^2$, and for a solid sphere, $I'=\frac{2}{5}mR^2$. Thus, the conservation of mechanical energy for spherical shell is as below: \begin{align*}E_i&=E_f \\\\ mgH&=\frac{1}{2}\left(\frac{2}{3}\right)mR^2{\left(\frac{V}{R}\right)}^2+\frac{1}{2}mV^2\\\\&=\frac{5}{6}mV^2 \\\\ \Rightarrow \quad V&=\sqrt{\frac{6}{5}gH}\end{align*}
Similarly, the conservation of mechanical energy for solid sphere is written as below \begin{align*} E_i&=E_f\\\\ mgH&=\frac{1}{2}\left(\frac{2}{5}\right)mR^2{\left(\frac{V'}{R}\right)}^2+\frac{1}{2}m{V'}^2\\&=\frac{7}{10}m{V^{'}}^2\\\\ \Rightarrow\quad V'&=\sqrt{\frac{10}{7}gH}\end{align*} Therefore, the ratio between the two distances are as follows \begin{align*} \frac{L}{L'}&=\frac{V}{V'}\\\\&=\frac{\sqrt{\frac{6}{5}gH}}{\sqrt{\frac{10}{7}gH}}\\\\&=\sqrt{\frac{42}{50}}\\\\ \Rightarrow \quad \frac{L'}{L}&=1.09\end{align*}
The magnitude of a single force acting on a particle of mass m is given by $F=bx^2$, where $b$ is a constant. The particle starts from rest. After it travels a distance $L$, determines its
(a) Kinetic energy and
(b) Speed
(a) Work-energy theorem states that $\Delta K=k_f-K_i=W_{net}$, where $W_{net}$ is the total work done on the system. Work is related to force by the formula $W=\int{\vec{F}\cdot d\vec{x}}$
\begin{align*}W=\int^L_0{\vec{F}\cdot d\vec{x}}&=\int^L_0{F\,dx\,{\cos 0^\circ}}\\&=\int^L_0{bx^2dx}\\&=\frac{1}{3}b{\left.x^3\right|}^L_0\\&=\frac{1}{3}bL^3\end{align*} Particle starts at rest, so $K_i=0$.
\[K_f-K_i=W\Rightarrow K_f=\frac{bL^3}{3}\]
(b) Solving $K_f$ for speed, we obtain
\begin{gather*} K_f=\frac{1}{2}mV^2_f=\frac{bL^3}{3} \\\\ \Rightarrow \quad V_f=\sqrt{\frac{2}{3}\frac{bL^3}{m}}\end{gather*}
A box of mass $M$ is at rest at the bottom of a frictionless inclined plane. The box is attached to a string that pulls with a constant tension $T$.
(a) Find the work done by the tension $T$ as the box moves through a distance $x$ along the plane.
(b) Find the speed of the box as a function of $x$.
(c) Determine the power delivered by the tension in the string as a function of $x$.
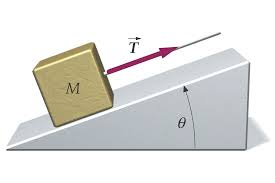
(a) Because the tension along the path is constant and parallel to the direction of motion so the physical work done by it is given by \[W_T=\int^x_0{\vec{F}.d\vec{l}}=\int^x_0{T\,dl}=Tx\]
For more problems on work in physics, refer to the following:
Work problems in physics
(b) Use the work-energy theorem to find the speed of the box.
\[K_f-K_i=W_{tot}=W_{weight}+W_{Tension}\]
\[W_{weight}=\int^x_0{{\vec{F}}_g \cdot d\vec{l}}= \begin{cases} \int^x_0{\left(mg\,{\sin \theta }\right)dx\, \cos 180^\circ} &=-mg\,x\,{\sin \theta } \\ \\ \int^x_0{\left(mg\,{\cos \theta }\right)dx\,\cos 90^\circ} & =0 \end{cases}\] The box starts at rest, $K_i=0$ so \begin{gather*}\frac{1}{2}mV^2_f=-mg\,x\,{\sin \theta\ }+Tx\\ \\ \Rightarrow V_f={\left(\frac{2Tx}{m}-2gx\,{\sin \theta\ }\right)}^{\frac{1}{2}}\end{gather*}
(c) Power is defined as the rate of the work done by the system \begin{gather*} P=\frac{dW}{dt}=\frac{d}{dt} \vec{F}\cdot\vec{x} \\\\ \xrightarrow{F\ is\ constant} P=\vec{F}\cdot\frac{dx}{dt}=\vec{F}\cdot\vec{x}=\vec{F}\cdot\vec{V} \end{gather*}
In this problem, $\vec{T}$ and $\vec{V}$ are parallel (weight is normal to velocity), so \[P=TV=T{\left(\frac{2Tx}{m}-2gx\,{\sin \theta}\right)}^\frac 12\]
An Atwood's machine consists of masses $m_1$ and $m_2$, and a pulley of  negligible mass and friction. Starting from rest, the speed of the two masses is $4.0\, {\rm m/s}$ at the end of $3.0\, {\rm s}$. At that time, the kinetic energy of the system is $80\, {\rm J}$ and each masses has moved a distance of $6.0\, {\rm m}$. Determine the values of $m_1$ and $m_2$.
negligible mass and friction. Starting from rest, the speed of the two masses is $4.0\, {\rm m/s}$ at the end of $3.0\, {\rm s}$. At that time, the kinetic energy of the system is $80\, {\rm J}$ and each masses has moved a distance of $6.0\, {\rm m}$. Determine the values of $m_1$ and $m_2$.
Apply work-energy theorem: $\Delta K=K_f-K_i=W_{tot}$
Starting from rest, i.e. $K_i=0$. Because the masses 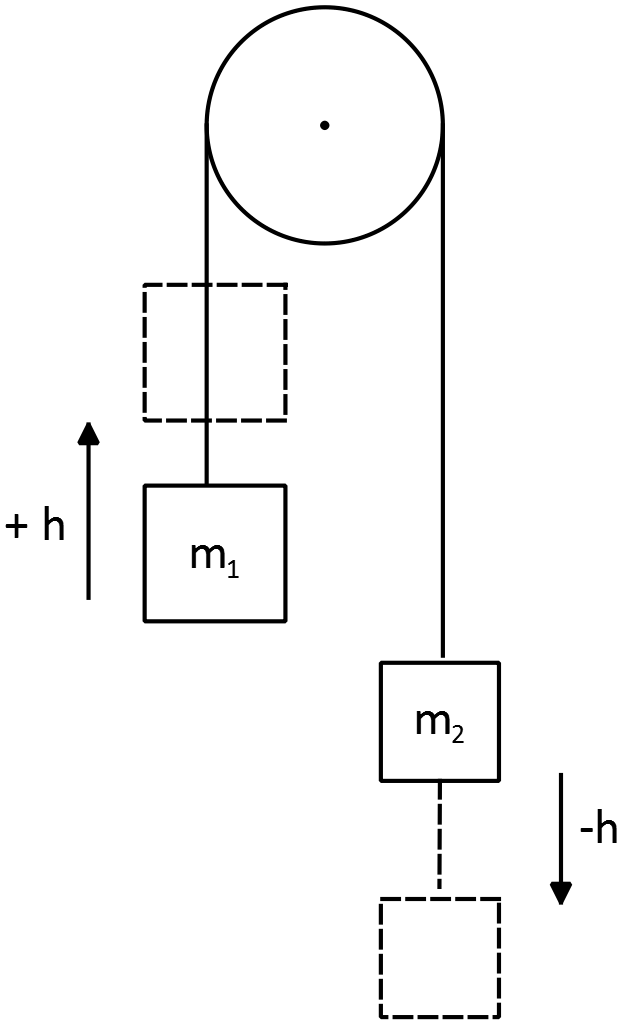 are moving in the opposite direction, so one of them has positive work and the other negative. Therefore
are moving in the opposite direction, so one of them has positive work and the other negative. Therefore
\[\left\{ \begin{array}{c} W_{tot}=m_1gh+\left(-m_2gh\right) \\ \Delta K=K_f-0=60{\rm J} \end{array} \right.\]
\[\Rightarrow 60=\left(m_1-m_2\right)gh\Rightarrow m_1-m_2=\frac{60}{gh}\ ,\ \ \ \left(*\right)\]
Where $h$ measures from the starting position.
The kinetic energy of the system after $3{\rm s}$ is $80\ {\rm J}$ .i.e.
\[K_f=\frac{1}{2}\left(m_1+m_2\right)v^2_f=80\Rightarrow m_1+m_2=\frac{160}{v^2_f}=\frac{160}{4^2}\ \ ,\ \ \left(**\right)\]
From (*) and (**):
\[\left\{ \begin{array}{c} m_1-m_2=\frac{60}{9.8\times 6}=1.36 \\ m_1+m_2=\frac{160}{4^2}=10 \end{array} \Rightarrow 2m_1=11.36\Rightarrow m_1=5.68{\rm kg}\ \right.\]
So $m_1+m_2=10\Rightarrow m_2=10-m_1=10-5.68=4.32{\rm kg}$
A block of mass $m$ rests on an inclined plane. The coefficient of static friction between the block and the plane is $\mu_{s}$. A gradually increasing force is pulling down on the spring (force constant $k$). Find the potential energy $U$ of the spring at the moment the block begins to move.
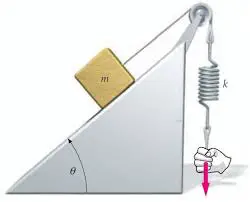
The free-body diagram of an object sliding on a ramp is as follows:
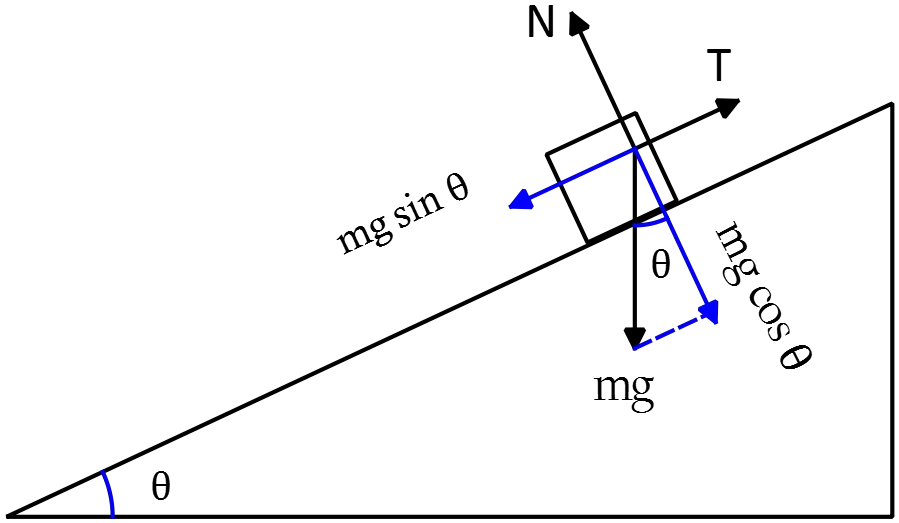
There is no movement in the perpendicular direction to the motion, i.e.,
\[\Sigma F_y=0\to N-mg\,{\cos \theta\ }=0\ \ ,\ \ (1)\]
On the other hand, along the inclined plane $\Sigma F_x=0$, since the block is at the threshold of the moving. \[\Rightarrow T-f-mg\,{\sin \theta\ }=0 \quad ,\quad (2)\] At the instant, the block begins to move, static friction has reached its maximum value, i.e. $f_{s,max}=\mu_{s}N=\mu_{s}mg\,{\cos \theta}$, thus, substituting this into $(2)$, we will have \[(2) \Rightarrow \ T=\mu_s mg\,{\cos \theta}+mg\,{\sin \theta}\]
If the spring is not accelerating, then the force pulling down must be equal to the tension force on the rope over the pulley so, $F_{spring}=kx$, where $x$ is the distance the spring is stretched. Therefore \begin{gather*} T=\mu_s mg\cos\theta+mg\sin\theta \\ T=kx \end{gather*} Equating these two expressions, we will have \[x=\frac{mg( \mu_s \cos\theta+\sin\theta)}{k}\]
The potential energy stored in the spring is calculated as follows \begin{align*} U_{spring}&=\frac{1}{2}kx^2 \\\\ &=\frac{1}{2k}[mg\left(\sin \theta+\mu_{s}\,\cos \theta)\right]^2\end{align*}
A box of mass $m$ on the floor is connected to a horizontal spring of force constant $k$. The coefficient of kinetic friction between the box and the floor is $\mu_k$. The other end of the spring is connected to a wall. The spring is initially unstressed. If the box is pulled away from the wall a distance $d_0$ and released, the box slides toward the wall. Assume the box does not slide so far that the coils of the spring touch.
(a) Obtain an expression for the distance $d_1$ the box slides before it first comes to a stop.
(b) Assuming $d_1>d_0$, obtain an expression for the speed of the box when it has slid a distance $d_0$ following the release.
(c) Obtain the special value of $\mu_k$ such that $d_1=d_0$.
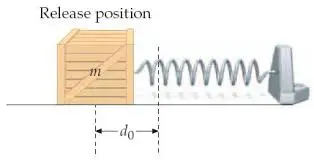
(a) Use conservation of mechanical energy in the presence of dissipating forces like friction. i.e. $\Delta E=E_f-E_i=W_f$, where $W_f$ is the work done by these forces.
Initially the box is at rest, $K_i=0$ and the spring is stretched, $U_{i,s}=\frac{1}{2}kd^2_0$.
When it comes to a stop, $K_f=0$ again and the final potential energy of the spring is $U_{f,s}=\frac{1}{2}k{\left(\Delta x\right)}^2$, where $\Delta x=d_1-d_0$ is the final displacement of the spring from equilibrium position.
Kinetic friction has done work over the block in this path so
\[W_{friction}=-f{{\rm d}}_{{\rm 1}}=-\mu_{k}mg\,d_1\]
Therefore:
\[E_f-E_i=W_f\to \left(U_f+K_f\right)-\left(U_i+K_i\right)=W_f\]
\[\frac{1}{2}k{\left(d_1-d_0\right)}^2-\frac{1}{2}kd^2_0=-\mu_{k}mg\,d_1\]
\[d^2_0-d^2_1+2d_1d_0-d^2_0=2\mu_{k}\,mg\,d_1\Rightarrow d_1=2d_0-2\mu_{k}\frac{mg}{k}\]
(b) Use conservation of mechanical energy, $\Delta E=W_f$
When the box reaches $d_0$ there is no spring potential energy (the box is on the equilibrium position) i.e. $U_{f,s}=\frac{1}{2}kd^2_0$ but at this point the box has velocity i.e. $K_f=\frac{1}{2}mv_{f2}$
\[E_f-E_i=W_f\Rightarrow \left(0+\frac{1}{2}mv^2_f\right)-\left(\frac{1}{2}kd^2_0+0\right)=-\mu_{k}mg\,d_0\]
\[v_f={\left(2\frac{k}{m}d^2_0-2\mu_kg\,d_0\right)}^{\frac{1}{2}}\]
\[\ \]
(c) Setting $d_1=d_0$ in the result of part (a) and solving for $\mu_k$, we obtain
$$d_1=2d_0-2\mu_k\frac{mg}{k}\ \ \xrightarrow{d_0=d_1} \mu_k=\frac{kd_0}{2mg}\ $$
A $5.00\,{\rm kg}$ block is firmly attached to a $120\,{\rm N/m}$ spring. The block is initially at rest and the entire setup is on a frictionless surface. A rope inclined at $36.9{}^\circ $ above the horizontal is used to slowly pull the block until the block-spring-rope system is again at rest. At this point, the spring is stretched by $40.0\, {\rm cm}$.
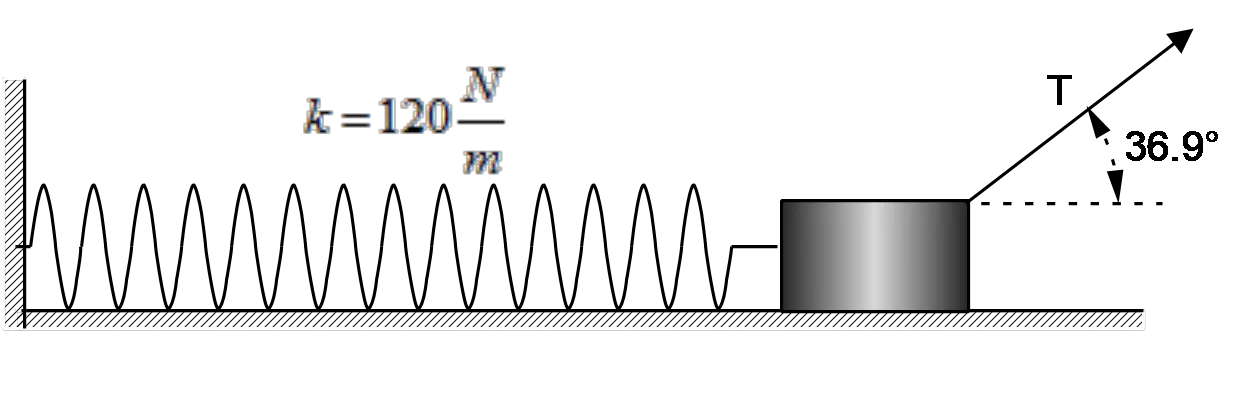
(a) Calculate the tension in the rope at this point( spring stretched by $40.0\, {\rm cm}$)
(b) Calculate the work done by the tension in the rope as the block moves from its initial position to this point.( spring stretched by $40.0\, {\rm cm}$)
(c) Suddenly the rope breaks. Calculate the speed of the block at the point where the spring is once again upstretched-uncompressed.
(a) Because at this point the system is at rest so \begin{gather*}\Sigma F_x=0\Rightarrow T{\cos 36.9^\circ}-kx=0\\\\ \Rightarrow T=\frac{kx}{{\cos 36.9{}^\circ \ }}=\frac{120\times 0.40}{{\cos 36.9{}^\circ \ }}=60.02\ {\rm N}\end{gather*}
(b) This part is related to the work-energy theorem problem. According to this theorem, we have $K_f-K_i=W_{net}$. Because the block is initially at rest and after $x=0.4\ {\rm m}$ again come to a stop, so $K_i=K_f=0$.
\[\Delta K=W_{net}\Rightarrow 0-0=W_T+W_s\]
Where $W_s=-\frac{1}{2}kx^2$ is the work done by the spring on the block and $x$ is distance to equilibrium. Therefore, \[W_T=\frac{1}{2}kx^2=\frac{1}{2}(120)(0.4)^2=9.6\quad {\rm J}\]
Important note: we cannot use the definition of the work done by a constant force $F$ on an object over a distance $x$ that is $W=\vec{F}\cdot d\vec{x}$, because, in this case, block attached to spring and so the tension in the rope is not a constant force so $W\ne \vec{T}\cdot d\vec{x}$.
(c) Use the conservation of mechanical energy between the instant that the rope breaks and when it is reached an equilibrium. \begin{gather*} E_2-E_1=W_{NC}=0 \quad \Rightarrow\quad E_2=E_1\\\\ K_2+U_2=K_1+U_1 \\\\ \frac{1}{2}mv^2_2+0=0+\frac{1}{2}kx^2 \\\\ \Rightarrow v=\sqrt{\frac{k}{m}}x=\sqrt{\frac{120}{5}}\left(0.4\right)=1.96\,{\rm \frac ms} \end{gather*}
In the above, $W_{NC}$ is the work done by the non-conservative forces such as friction.
Note: the potential energy stored in the spring is the negative of the work done by it that is \[U_s=-W_s=\frac{1}{2}kx^2\]
In the system drawn below, the coefficient of kinetic friction between the $6.00\, {\rm kg}$ block and the horizontal surface is $0.15$, and the entire system is being held at rest (by someone who is holding the hanging $2.00\, {\rm kg}$ block in place). This person releases the block. Calculate the speed of each block after the $2.00\, {\rm kg}$ block has fallen $30.0\, {\rm cm}$.
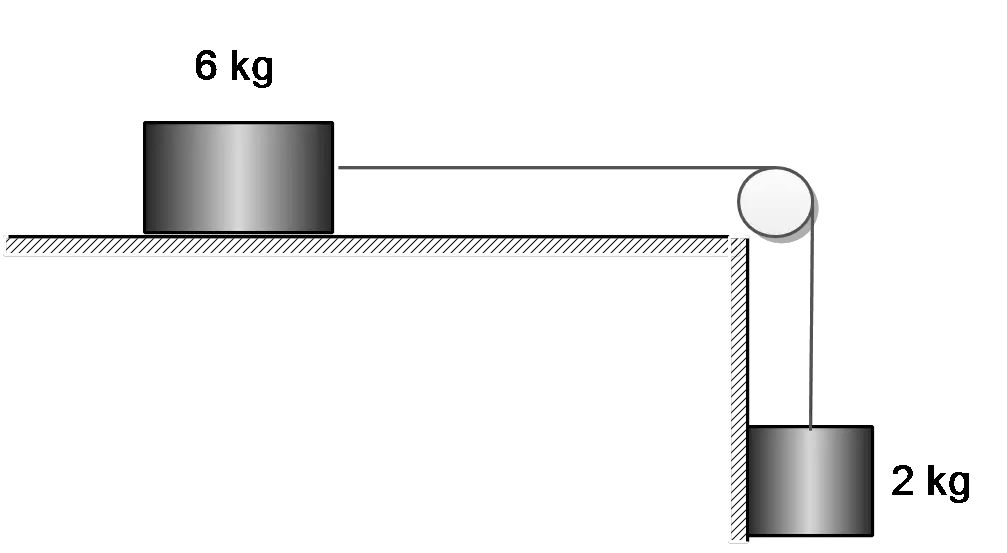
Because there is a non-conservative force acting on the $6\, {\rm kg}$ block so we must use the following version of conservation of the mechanical energy:
\[E_2-E_1=W_{NC}\]
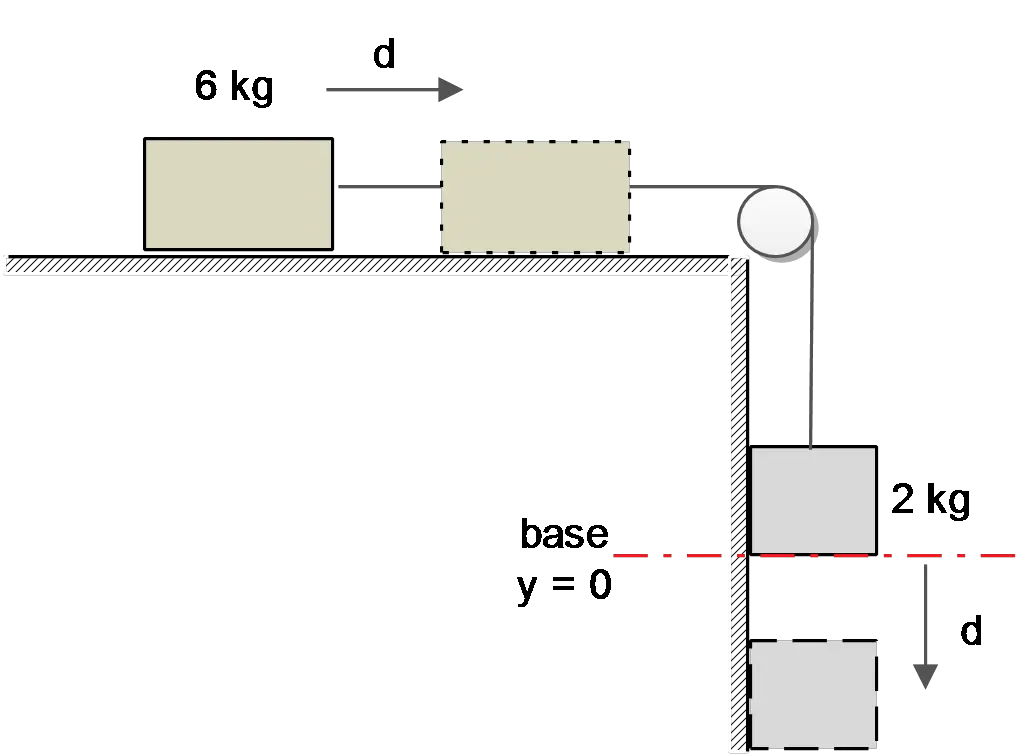
Let the initial position of the blocks be the origin of the coordinate systems, so the $2\, {\rm kg}$ block moves downward the coordinate. Conservation of energy gives,
\begin{gather*} E_f-E_i=W_f\\ \to \left(U_f+K_f\right)-\left(U_i+K_i\right)=-fd \end{gather*}
Where $d$ is the distance that the $6\ {\rm kg}$ block moves (or both blocks moves!)
\begin{gather*}\left(-m_2gd+\frac{1}{2}\left(m_6+m_2\right)v^2_f\right)-\left(0+0\right)=-\mu_km_6gd\\\Rightarrow \frac{1}{2}\left(m_6+m_2\right)v^2_f=gd\left(m_2-\mu_km_6\right)\\\end{gather*} Therefore, the final speed is obtained by solving the above equation for $v_f$
\begin{align*} v_f&=\sqrt{\frac{2gd\left(m_2-\mu_km_6\right)}{m_6+m_2}}\\\\&=\sqrt{\frac{2\times 9.8\times 0.30\times (2-0.15\times 6)}{6+2}}\\\\&=0.899\quad {\rm \frac ms} \end{align*}
Note: the friction work is always $W_f=-fd=\mu_kNd$, where $N$ is the normal force and $d$ is the displacement of the object.
Note: the $2\, {\rm kg}$ object is moving down the origin so its potential energy must be negative.
An $80\, {\rm g}$ arrow is fired from a bow whose string exerts an average force of $95\, {\rm N}$ on the arrow over a distance of $80\, {\rm cm}$. What is the speed of the arrow as it leaves the bow?
Use the work-kinetic energy theorem: $\Delta K=K_f-K_i=W_{net}$, where $W_{net}$ is the sum of works done on the object in the displacement $x$. Therefore,
\begin{align*}\frac{1}{2}m(v^2_f-v^2_i)&=Fx \\\\ \Rightarrow \quad v_f&=\sqrt{\frac{2Fx}{m}} \\\\ &=\sqrt{\frac{2\times 95\times 0.80}{0.080}} \\\\ &=44\quad \rm m/s \end{align*}
A force $\vec{F}=12\,\hat{i}-10\,hat{j}\,{\rm (N)}$ acts on an object. How much work does this force do as the objects moves from the origin to the point $\vec{r}=12\,\hat{i}+11\,\hat{j}\ {\rm (m)}$
By definition, the work done by a constant force $\vec{F}$ over a distance $\vec{x}$ is scalar product of vector force by the displacement vector $W=\vec{F}\cdot \vec{x}$ so \begin{align*} W&=(12\,\hat{i}-10\,\hat{j})\cdot (12\,\hat{i}+11\,\hat{j})\\ &=144(\hat{i}\cdot \hat{i})-110(\hat{j}\cdot \hat{j})\\ &=144-110\\ &=34\quad {\rm J} \end{align*} Note: the dot product or inner product of the unit vectors are defined as \[\hat{i}\cdot \hat{i}=|\hat{i}||\hat{i}|{\cos 0{}^\circ}=1\] And so on \[\hat{j}\cdot \hat{j}=\hat{k}\cdot\hat{k}=1\] And similarly, \[\hat{i}\cdot\hat{j}=|\hat{i}||\hat{j}|{\cos 90{}^\circ}=0\]
In the figure, a constant external force $P=160\, {\rm N}$ is applied to a $20\, {\rm kg}$ box, which is on a rough horizontal surface. While the force pushes the box a distance of $8\, {\rm m}$, the speed changes from $0.5\, {\rm m/s}$ to $2.6\, {\rm m/s}$. What is the work done by friction during this process?
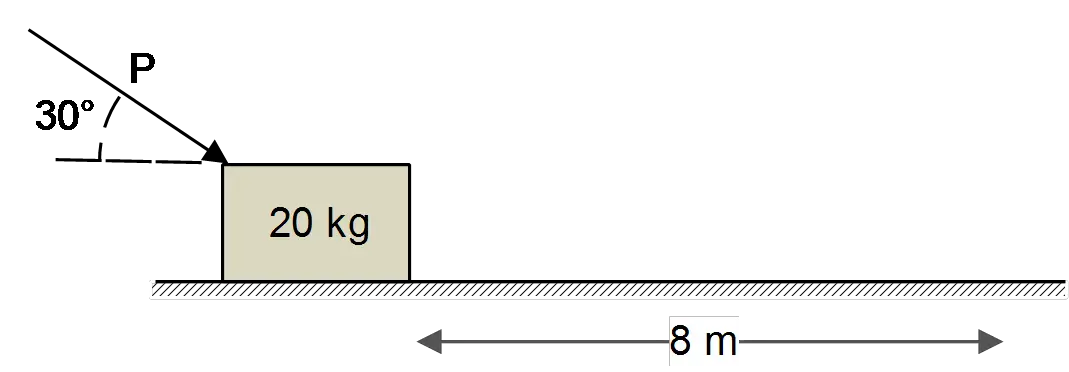
Use the work-energy theorem $\Delta K=W_{net}$, where $W_{net}$ is the total work done on an object. In this case, there are two works, due to the constant force and friction. First calculate the work $W_P$ and substitute it in the $\Delta K=W_{net}$, then solve for $W_f$.
\[W_P=P\left|x\right|{\cos \theta\ }=160\left(8\right){\cos 30{}^\circ \ }=1108.51\ {\rm J}\]
\[K_f-K_i=W_f+W_P\Rightarrow \frac{1}{2}m\left(v^2_f-v^2_i\right)=W_f+W_P\]
\[\frac{1}{2}\left(20\right)\left({\left(2.6\right)}^2-{\left(0.5\right)}^2\right)=W_f+1108.51\Rightarrow W_f=-1043.41\ {\rm J}\]
A net force along the $x$ axis $F\left(x\right)=-C+Dx^2$ is applied to a mass of $m$ that is initially at the origin moving in the $-x$ direction with a speed of $v_0$. What is the speed of the object when it reaches a point $x_f$?
Use the work-energy theorem but in this case, we have a varying force so
\[K_f-K_i=W_{net}=\int^{x_f}_{x_i}{F\left(x\right)dx}\]
\[\Rightarrow \frac{1}{2}m\left(v^2_f-v^2_i\right)=\int^{x_f}_{x_i=0}{\left(-C+Dx^2\right)dx}={\left(-Cx+\frac{D}{3}x^3\right)}^{x_f}_{x_i=0}\]
\[\Rightarrow v_f=\sqrt{v^2_0+\frac{2}{m}\left(-Cx_f+\frac{D}{3}x^3_f\right)}\ \ \]
A body of mass $M$ is seated on top of a hemispherical mound of ice of radius $R$ as shown below. He starts to slide down the ice and eventually flies off the mound of ice. The ice is frictionless. 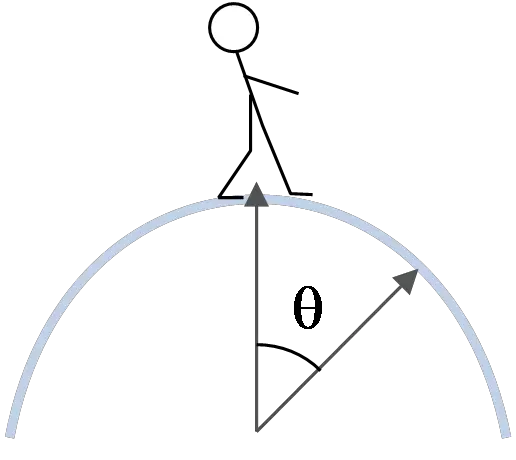
(a) Draw a free body diagram for the boy when he is at point $P$.
(b) At angle $\theta$, what is the boy's velocity?
(c) What is $\theta_0$ the angle at which the boy flies off the ice mound?
(a) There are two forces acting on the boy, one is the normal force and the other is gravity as shown in the figure below.
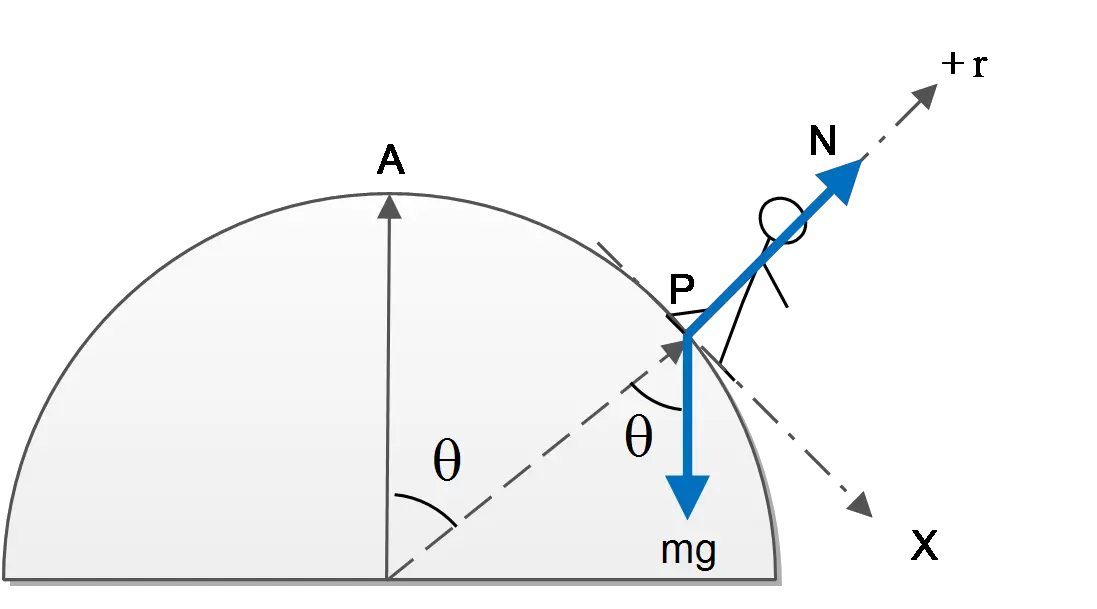
(b) Use the conservation of mechanical energy between points $A$ and $P$. Consider the center of the hemisphere as the reference level so at $P$ the distance to the base is $h=R\, \cos \theta$
\[E_A=E_P\Rightarrow U_A+K_A=U_P+K_P\]
\[\Rightarrow \ \ mgR=mgR\,{\cos \theta\ }+\frac{1}{2}mv^2_P\ \]
\[\Rightarrow v_P=\sqrt{2gR(1-{\cos \theta\ })}\]
This is the velocity of the boy everywhere on the hemisphere.
(c) When the normal force acting on the boy reaches zero, then the boy flies off. So first apply Newton's 2${}^{nd}$ law on the boy at point $P$, then set $N=0$:
\[\Sigma F_r=ma_r\Rightarrow N\hat{r}+mg\,{\cos \theta\ }\left(-\hat{r}\right)=\frac{mv^2}{R}\left(-\hat{r}\right)\]
\[\Rightarrow mg\,{\cos \theta\ }-N=\frac{mv^2}{R}\xrightarrow{N=0} v=\sqrt{Rg\,{\cos \theta\ }}\]
Note: we have used the polar coordinate. The centripetal acceleration is always towards the center i.e. $-\hat{r}$
In part (b) we have found the velocity of the boy at an arbitrary angle $\theta$. In part (c) the velocity at instant the boy flies off have found. Now set equal these velocities with each other to determine the angle at which the boy files off.
\[\sqrt{2gR\,\left(1-{\cos \theta\ }\right)}=\sqrt{Rg\,{\cos \theta\ }}\Rightarrow 2gR\,\left(1-{\cos \theta\ }\right)=Rg\,{\cos \theta\ }\]
\[\Rightarrow 2Rg=3Rg\,{\cos \theta\ }\Rightarrow \theta={{\cos }^{-1} \left(\frac{2}{3}\right)\ }\ \sim \ 48.19{}^\circ \]
A uniform solid sphere is rolling without slipping along a horizontal surface with a speed of $4.5\, {\rm m/s}$ when it starts up a ramp that makes an angle of $25{}^\circ $ with the horizontal. What is the speed of the sphere after it has rolled $3.00\, {\rm m}$ up the ramp, measured along the surface of the ramp?
Use the conservation of mechanical energy as $E_i=E_f$.
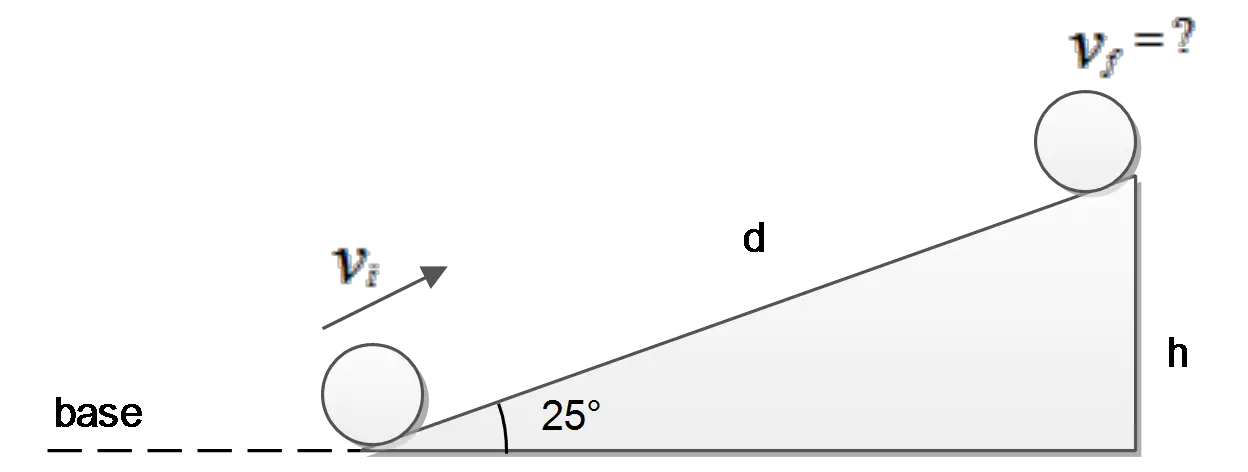
Here there is a rotational kinetic energy due to the rolling of the sphere, therefore
\[\frac{1}{2}mv^2_i+\frac{1}{2}I\omega^2+mgh=\frac{1}{2}mv^2_f+\frac{1}{2}I\omega^2+0\]
Where $I$ is the moment of inertial that for a sphere is $\frac{2}{5}mR^2$. Recall that in the rotational motion the angular velocity is related to the linear velocity via $v=r\omega$ so
\[\frac{1}{2}mv^2_i+\frac{1}{2}\left(\frac{2}{5}mR^2\right){\left(\frac{v_i}{R}\right)}^2+0=\frac{1}{2}mv^2_f+\frac{1}{2}\left(\frac{2}{5}mR^2\right){\left(\frac{v_f}{R}\right)}^2++mgd\,{\sin 25{}^\circ \ }\]
\[\frac{7}{10}mv^2_i=\frac{7}{10}mv^2_f+mgd\,{\sin 25{}^\circ \ }\Rightarrow v_f=\sqrt{v^2_i-\frac{10}{7}gd\,{\sin 25{}^\circ \ }}\]
\[\Rightarrow v_f=\sqrt{{\left(4.5\right)}^2-\frac{10}{7}\left(9.8\right)\left(3\right){\sin 25{}^\circ \ }}=1.58\frac{{\rm m}}{{\rm s}}\]
A huge cannon is assembled on an airless planet having insignificant axial spin. The planet has a radius of $5\times {10}^6\, {\rm m}$ and a mass of $3.95\times {10}^{23}\,{\rm \ kg}$. The cannon fires a projectile straight up at $2000\, {\rm m/s}$. An observation satellite orbits the planet at a height of $1000\, {\rm km}$. What is the projectile's speed as it passes the satellite?
Use the conservation of mechanical energy to find the desired speed.
\[E_1=E_2\Rightarrow \frac{1}{2}mv^2_1-\frac{GmM}{r_1}=\frac{1}{2}mv^2_2-\frac{GMm}{r_2}\]
Where the second term is the gravitational potential of an object of mass $m$ at a distance $r\ $from the center of a planet with mass $M$.
\[v^2_1-\frac{2GM}{r_1}=v^2_2-\frac{2GM}{r_2}\Rightarrow v_2=\sqrt{v^2_1+2GM\left(\frac{1}{R+h}-\frac{1}{R}\right)}\]
\[\Rightarrow v_2=\sqrt{{\left(2000\right)}^2+2\left(6.67\times {10}^{-11}\right)\left(3.95\times {10}^{23}\right)\left(\frac{1}{\left(5\times {10}^6+{10}^6\right)}-\frac{1}{5\times {10}^6}\right)}=1498\frac{{\rm m}}{{\rm s}}\]
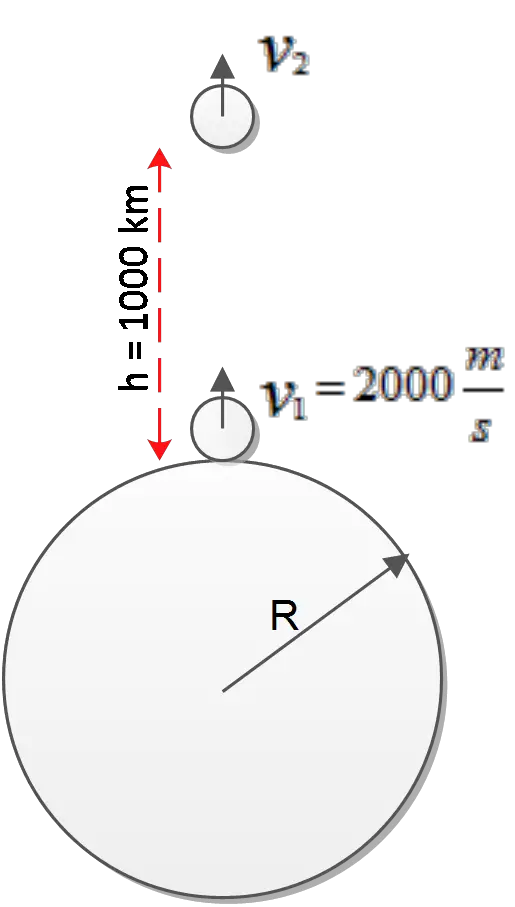
Note: the gravitational potential energy is equal to the work done against the gravity of an object with mass $M$ to bring a unit mass $m$ to a given point say $r$ from the center of it .so
\[U=-\frac{GmM}{r}\]
Where $G=6.67\times {10}^{-11}\, \rm N\cdot m^2/kg^2$ is the gravitational constant.
A roller coaster cart rolls from rest down a ${\rm 50.0\, m}$ tall hill and then goes around a circular vertical loop-the-loop of radius ${\rm 15.0\, m}$ as shown at right.
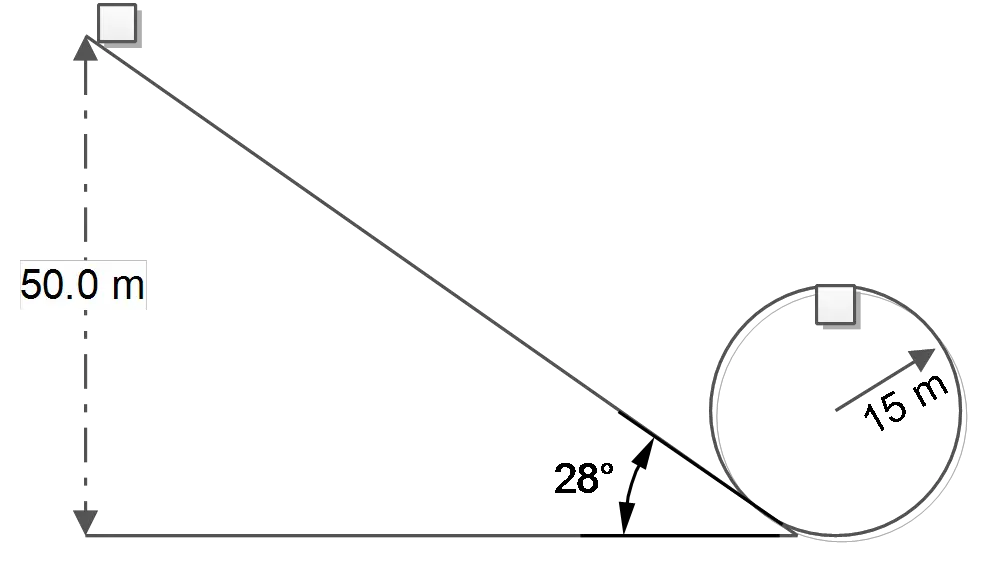
(a) How fast is the cart going when it gets to the top of the loop?
(b) If the mass of the cart (including all of its passengers) is $1.2\times 10^3\,\rm kg$, what is the magnitude of the normal force that acts on the cart at the top of the loop?
(a) Use the conservation of the mechanical energy between starting point $i$ and top of the loop $t$. (let the lowest point of the circle as the base)
\[E_i=E_t\Rightarrow U_i+K_i=U_t+K_t\Rightarrow \ mgh+0=mg\left(2R\right)+\frac{1}{2}mv^2_t\]
\[v_t=\sqrt{2g(h-2R)}=\sqrt{2\left(9.8\right)\left(50-2\left(15\right)\right)}=19.79\ {\rm m/s}\]
(b) There is a centripetal force acting on the cart provided by the normal force 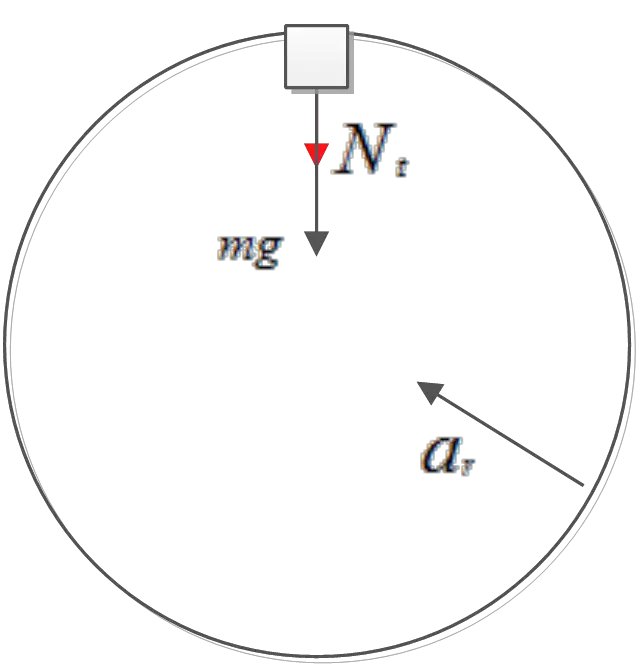 in the circular path. Recall that this force always is in direction of the center of the circle ($-\hat{r}$). So apply Newton's 2${}^{nd}$ law to the cart
in the circular path. Recall that this force always is in direction of the center of the circle ($-\hat{r}$). So apply Newton's 2${}^{nd}$ law to the cart
\[\Sigma {\vec{F}}_r=m{\vec{a}}_r\Rightarrow N\left(-\hat{r}\right)+mg\left(-\hat{r}\right)=\frac{mv^2}{2}\left(-\hat{r}\right)\]
\[N=\frac{mv^2}{r}-mg\]
Thus the normal force is, in general, as above. Put the velocity of the top point of the loop to find the normal force at that point
\[N=\frac{mv^2_t}{r}-mg=\left(1.2\times {10}^3\right)\left(\frac{{\left(19.79\right)}^2}{15}-9.8\right)\ \sim \ 19.6\ {\rm kN}\]
A uniform solid sphere of radius $r$starts from rest at a height $h$ and rolls without slipping along the loop track of radius $R$ as shown in the figure. ($r\ll R$).
(a) Draw the free body diagram for the sphere when it is at the top of the loop (point A) and moving fast enough to stay on the truck.
(b) What is the smallest height $h$ for which the sphere will not leave the truck at the top?
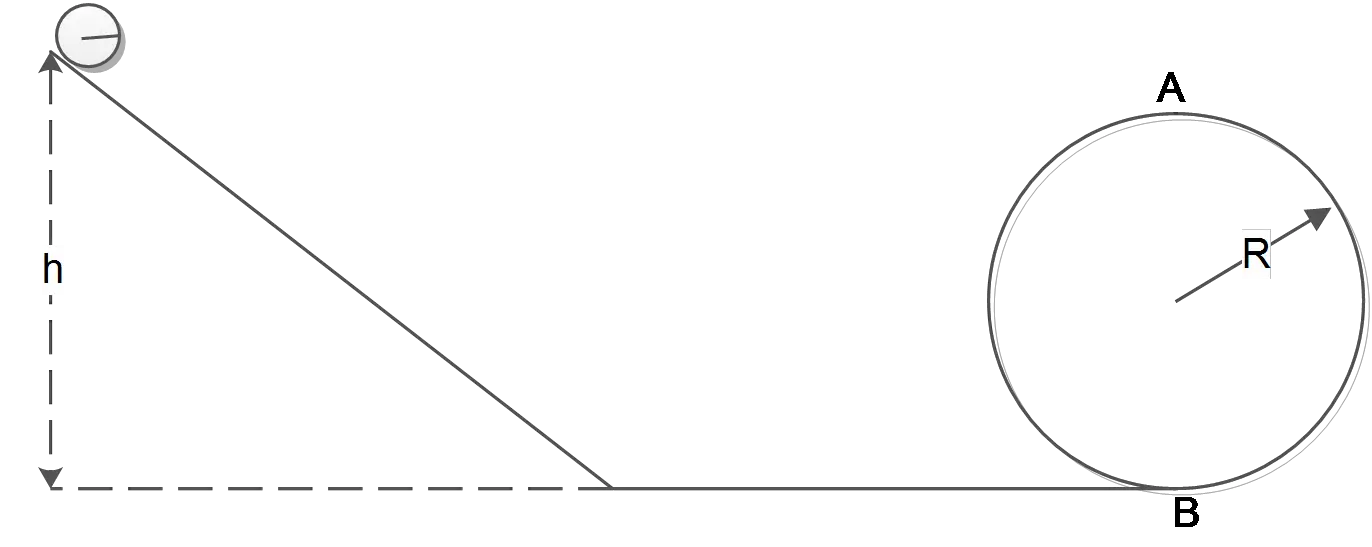
(a) Rolls without slipping means that the point of the contact of the object with the ground does not move. This type of motion is provided by static 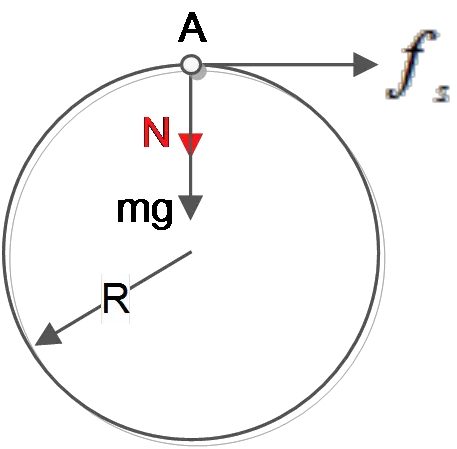 friction. Therefore, three forces act on the sphere. Gravity, normal force, and static friction.
friction. Therefore, three forces act on the sphere. Gravity, normal force, and static friction.
(b) The static force does not any work on the sphere since the sphere instantaneously does not slide but rolls! Therefore, use the conservation of mechanical energy to find the desired height.
\[E_f-E_i=W_{NC}=0\Rightarrow E_f=E_i\]
\[mgh=\frac{1}{2}mv^2_A+\frac{1}{2}I\omega^2+mg\left(2R\right)\]
If substitute $I=\frac{2}{5}mr^2$ and $\omega=v/r$ then we obtain
\[mgh=\frac{1}{2}mv^2_A+\frac{1}{2}\left(\frac{2}{5}mr^2\right){\left(\frac{v_A}{r}\right)}^2+mg\left(2R\right)\Rightarrow gh=\frac{7}{10}v^2_A+2gR\]
Now apply Newton's 2${}^{nd}$ law in the circular motion at the point A to find the $v_A$
\[\Sigma F_r=ma_r\Rightarrow N+mg=\frac{mv^2_A}{R}\ \]
If we set $N=0$, we find the minimum value of $v_A$ so $v^{min}_A=\sqrt{Rg}$. Put this value into the relation above
\[gh=\frac{7}{10}\left(Rg\right)+2gR\Rightarrow \ \ h_{min}=2.7R\]
An $8\, {\rm kg}$ block is released from rest, $v_1=0\, {\rm m/s}$, on a rough incline. The block moves a distance of $1.6\, {\rm m}$ down the incline, in a time interval of $0.8\, {\rm s}$, and acquires a velocity of $v_2=4.0\, {\rm m/s}$.
(a) Calculate the works done by the weight, friction, and normal forces.
(b) What is the average rate at which the block gains kinetic energy during the $0.8\, {\rm s}$ time interval?
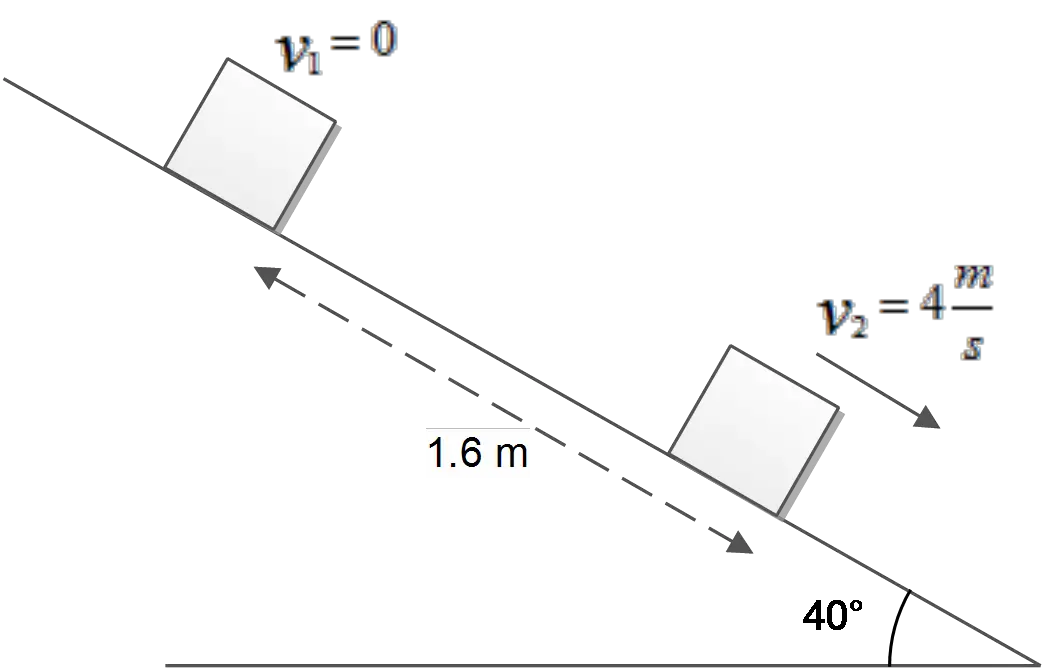
(a) By definition, the work done by a constant force $\vec{F}$ is the product of the magnitude $\Delta \vec x$ of the displacement of the point of application of the force and the component of the force along the direction of the displacement that is $F{\cos \theta\ }$. Therefore
\[W=\vec F.\Delta \vec x=F\left|\Delta x\right|{\cos \theta\ }\]
First, draw all of the forces act on a body on an incline plane as shown in the figure. Recall that the components along the direction of the displacement does work and the components perpendicular to the displacement does not work (since the angle between force and displacement is $\theta=90{}^\circ $)
\[W_g=\left(\underbrace{mg\,{\sin 40{}^\circ \ }}_{F_{\parallel }}\right)\times 1.6\times {\cos 0{}^\circ \ }=8\times 9.8\times {\sin 40{}^\circ \ }\times 1.6=+80\ {\rm J}\]
\[W_N=Nx\,{\cos 90{}^\circ \ }=0\]
\[W_f=fx\,{\cos 180{}^\circ \ }=-fx=-\mu_kNx\]
Since the coefficient of kinetic friction have not given so we must find the work done by the friction by applying the work-energy theorem as follows
\[\Delta K=W_{tot}=W_g+W_N+W_f\]
\[\frac{1}{2}m\left(V^2_2-V^2_1\right)=W_g+W_f+W_N\Rightarrow \frac{1}{2}\left(8\right)\left(4^2-0^2\right)=80+W_f+0\]
\[W_f=-16\ {\rm J}\]
(b) The time rate at which a force does work is called Power. Therefore, calculate the change in the kinetic energy of the block then use the definition of the power to find it
\[P=\frac{energy}{time}\]
\[P=\frac{\Delta K}{\Delta t}=\frac{\frac{1}{2}m\left(V^2_2-V^2_1\right)}{\Delta t}=\frac{\frac{1}{2}\left(4\right)\left(4^2-0^2\right)}{0.8}=80\ {\rm W}\]
Imagine a toy gun in which a ball is shot out when a spring is released. The force constant of the spring is $10\, {\rm N/m}$, and it is compressed by $0.05\, {\rm m}$. The mass of the ball is $0.02\, {\rm kg}$. If no energy is lost to friction, approximately what is the speed of the ball when it is shot out?
Initially, the spring is compressed so it has elastic potential energy. After shooting out all of its potential energy converts to kinetic energy. Using the conservation of mechanical, we obtain
\[E_f-E_i=W_{NC}\]
Where $W_{NC}$ is the work done by the non-conservative forces such as friction. In this case, $W_f=0$ so we have
\[E_f=E_i\]
\[\Rightarrow \underbrace{\frac{1}{2}kx^2_f}_{elastic\ potential}+\underbrace{\frac{1}{2}mv^2_f}_{kinetic\ energy}=\frac{1}{2}kx^2_i+\frac{1}{2}mv^2_i\]
When the spring reaches its unstretched length ($x=0$), the ball is shot. Therefore,
\[0+\frac{1}{2}mv^2_f=\frac{1}{2}kx^2+0\Rightarrow v_f=x\sqrt{\frac{k}{m}}=\left(0.05\right)\sqrt{\frac{10}{0.02}}=1.12\,\rm m/s\]
A $25\ {\rm kg}$ child plays on a swing having support ropes that are $3.0\ {\rm m}$ long. A friend pulls her back until the ropes are $45{}^\circ $ from the vertical and release her from rest.
(a) What is the height of the child above her lowest point, at the moment she is released?
(b) What is the potential energy for the child just as she is released, compared with the potential energy at the bottom of the swing?
(c) How fast will she be moving at the bottom of the swing?
(a) consider $h$ to be the height of the child from releasing point to the lowest point. From the sketch, we obtain 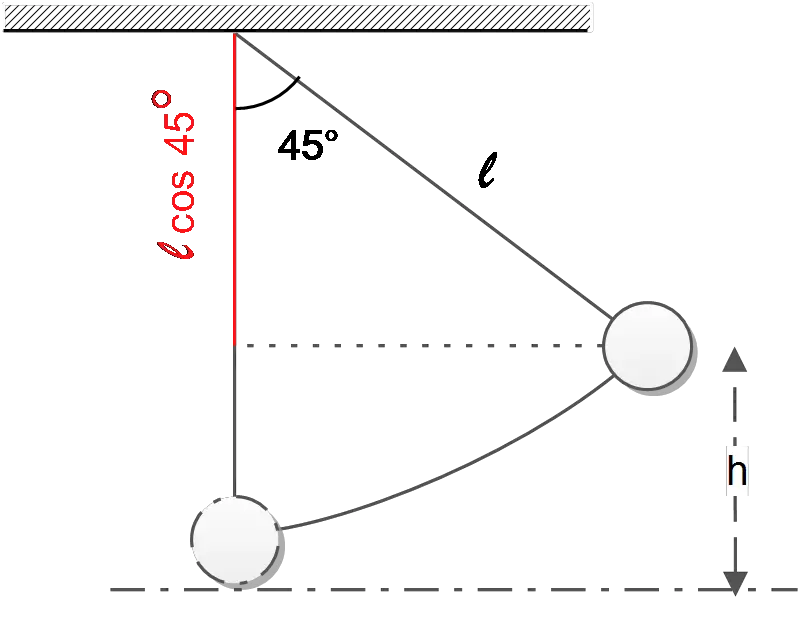
\[\ell\,cos\ 45{}^\circ +h=\ell \Rightarrow h=\ell\left(1-{\cos 45{}^\circ \ }\right)\]
\[\Rightarrow h=3\left(1-\frac{\sqrt{2}}{2}\right)=0.879\ {\rm m}\]
(b) The gravitational potential energy of mass $m$ at height $h$ is $U_{grav}=mgh$, so
\[U_{grav}=25\times 9.8\times 0.879=215\ {\rm J}\]
(c) Using the conservation of mechanical energy between the releasing point and the bottom of the swing, we get
\[E_{top}=E_{bot}\]
\[\Rightarrow mgh_i+\frac{1}{2}m\underbrace{v^2_i}_{v_i=0}=mg\underbrace{h_f}_{0}+\frac{1}{2}mv^2_f\]
\[\Rightarrow v_f=\sqrt{2gh}=\sqrt{2\times 9.8\times 0.879}=4.15\frac{{\rm m}}{{\rm s}}\]
A uniform solid cylinder starts from rest at a height of $1\ {\rm m}$ and rolls without slipping down a plane inclined at an angle of $20{}^\circ $ from the horizontal as shown.
(a) What is the speed of its center of mass when it reaches the bottom of the incline?
(b) What is the magnitude of the acceleration of its center of mass?
(c) What minimum coefficient of friction is required to prevent the cylinder from slipping?
(a) Since there is no friction in the system, so the mechanical energy of the cylinder is conserved so using this fact between initial and final points, we get \begin{gather*} E_i=E_f \\\\ mgh=\frac{1}{2}mv^2+\underbrace{\frac{1}{2}I\omega^2}_{\begin{array}{c}rotational \\ kinetic\ energy \end{array}}\end{gather*}
The required condition for rolling without slipping is $v=r\omega$ where $v$ is the tangential velocity of the cylinder (in this case the center of mass velocity) so
\begin{gather*}mgh=\frac{1}{2}mv^2+\frac{1}{2}\left(\frac{1}{2}mr^2\right){\left(\frac{v}{r}\right)}^2=\frac{3}{4}mv^2\\\\ \Rightarrow v_{CM}=\sqrt{\frac{4}{3}gh}\end{gather*}
Where we have used the moment of inertial of a hollow cylinder about the central axis i.e. $I_{cyl}=\frac{1}{2}mr^2$.
\[\Rightarrow v_{CM}=\sqrt{\frac{4}{3}(9.8)(1)}=3.61\, {\rm m/s}\]
(b) Now relate the initial and final velocities of the cylinder with the constant acceleration of it by the following equation
\begin{align*}v^2-v^2_0&=2a_{CM}\Delta s\\\\ \Rightarrow \ a_{CM}&=\frac{v^2}{2\Delta s}\\\\&=\frac{v^2{\sin 20^\circ}}{2h}\\\\&=\frac{{\left(3.61\right)}^2{\sin 20^\circ}}{2\times 1}\\\\&=2.23\,{\rm \frac{m}{s^2}}\end{align*}
From the geometry we see that the distance traveled by the cylinder $\Delta s$ is $h/{\sin 20^\circ}$.
(c) In part (b) the acceleration of the cylinder is obtained, so apply Newton's second law to the cylinder and find the desired quantity.
\begin{gather*} \Sigma F=ma\\\\ mg\,{\sin 20{}^\circ}-\mu_s\underbrace{mg\,{\cos 20^\circ}}_{N}=ma_{CM}\end{gather*} Solving the above for the unknown $\mu_s$, we have \begin{align*} \mu_s&=\frac{g\,{\sin 20^\circ}-a_{CM}}{g\,{\cos 20^\circ}}\\\\&=\frac{9.8\times {\sin 20^\circ}-2.23}{9.8\times {\cos 20^\circ}}\\\\&=0.121 \end{align*}
Important note: in the rolling without slipping motion, the ball is instantaneously at rest where it contacts the ground so we have used the static friction force equation.
Two rocks are thrown from a building $11\,{\rm m}$ high, each with a speed of $5\ {\rm m/s}$. one is thrown vertically upwards, the other horizontally. What is the speed at which each rock will hit the ground?
Solution 1 (kinematic language): use the kinematic relationships to find the speed of each rock after hitting the ground.
Let us consider the starting point as the reference point, thus the landing point has the coordinate ($x=?,y=-11\, {\rm m}$).
The first rock is thrown horizontally, so its motion is similar to a projectile with an angle of $\theta=0^\circ $. In the projectile motion, at every point, the velocity have two components as $v_x=v_{0x}=v_0\,{\cos \theta}$ and $v_y=v_0\,{\sin \theta}-gt$. Thus first calculate the elapsed time to the hitting point as follows
\begin{gather*} y=-\frac{1}{2}gt^2+v_0{\sin \theta}\ t+y_0 \\\\ -11=-\frac{1}{2}(9.8)t^2+5t\,{\sin 0^\circ}+0 \\\\ \Rightarrow \quad t_{tot}=\sqrt{\frac{22}{9.8}}=1.5\, {\rm s}\end{gather*}
Put it into the $y$ component of the velocity $v_y=5\,{\sin 0^\circ}-9.8\times 1.5=-14.7\, {\rm m/s}$. The negative indicates that the rock is moving toward the ground. Using the Pythagorean theorem, we get the velocity of the horizontally thrown rock as \begin{align*} v&=\sqrt{v^2_x+v^2_y} \\\\ &=\sqrt{(5\cos 0^\circ)^2+(-14.7)^2} \\\\ &=15.52\,\rm m/s \end{align*}
For the one which is thrown vertically, use the following kinematic relation to find its final velocity at the hitting point \begin{gather*} v^2-v^2_0=-2gh \\\\ v^2-5^2=-2(9.8)(-11) \\\\ \Rightarrow \quad v=15.52\, \rm m/s \end{gather*} As we can see, these two speeds are the same because they have the same mechanical energy at the moment of launch.
Solution 2 (energy approach):
\[E_i=E_f\Rightarrow \frac{1}{2}mv^2_i+mgh_i=mg\underbrace{h_f}_{0}+\frac{1}{2}mv^2_f\]
Dropping the mass of the rock and rearranging, we obtain
\[v_f=\sqrt{v^2_i+2gh_i}=\sqrt{5^2+2(9.8)(11)}=15.52\frac{{\rm m}}{{\rm s}}\]
Most useful formula for Work and Energy :
Definition of Work: $W=\vec F \cdot \vec s=Fs \,\rm{cos} \phi$
Kinetic energy: $K=\frac{1}{2}mv^2$
Work-Energy theorem : $W_{tot}=\Delta K=K_2-K_1$
Power: $P_{av}=\frac{\Delta W}{\Delta t}=\vec F \cdot \vec v$
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
