- Home
- Physics Problems
- Problems
Solved Problems
Three points charges are located on a circular arc as shown in the figure.
(a) What is the total electric field at P, the center of the arc?
(b) Find the electric force that would be exerted on an electron with charge $q=-e$ placed at P.
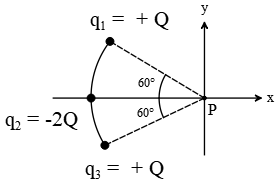
(a) First, find each of the electric fields, due to the charges, at P and then apply vector addition to calculate the resultant electric field at that point. We know that the electric field due to a point charge at distance $r$ from the source is given by
\[\vec E=\frac{1}{4\pi \epsilon_0} \frac{\left|q\right|}{r} \hat r\]
Where $\hat r$ is the unit vector lie along the line joining the source and the desired location of the field point. In some literature $\frac{1}{4\pi \epsilon_0}$ is called $k$. Therefore, \begin{gather*} {\vec{E}}_1=\frac{k\left|q_1\right|}{r^2_1}{\hat{r}}_1=\frac{kQ}{a^2}\left({\cos 60{}^\circ}\hat{i}+{\sin 60{}^\circ}(-\hat{j})\right)\\\\ {\vec{E}}_2=\frac{k\left|q_2\right|}{r^2_2}{\hat{r}}_2=\frac{k\left(2Q\right)}{a^2}(-\hat{i})\\\\ {\vec{E}}_3=\frac{k\left|q_3\right|}{r^2_3}{\hat{r}}_3=\frac{kQ}{a^2}({\cos 60{}^\circ}\hat{i}+{\sin 60{}^\circ}\hat{j})\\\\ {\vec{E}}_P={\vec{E}}_1+{\vec{E}}_2+{\vec{E}}_3=\frac{kQ}{a^2}2({\cos 60{}^\circ}-1)\hat{i}=-\frac{kQ}{a^2}\hat{i}\end{gather*}
(b) The force exerted on a charge $q$ in a uniform electric field is given by $\vec{F}=q\vec{E}$.
\[\vec{F}=q\vec{E}=\left(-e\right)\left(-\frac{kQ}{a^2}\right)\hat{i}=\frac{keQ}{a^2}\hat{i}\]
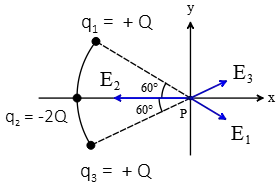
Note: the electric field of a negative point charge is toward the charge and away from the positive charge.
In the figure below, let $Q_1=+6.84\, \mu{\rm C}\ ,\ Q_2=-16.2\,\mu {\rm C}$ and $Q_3=+9.2\, \mu {\rm C}$ be rigidly fixed and separated by $r_{12}=r_{13}=r_{23}=1.34\, {\rm m}$. Calculate the electric potential at point P which is half-way between $Q_1$ and $Q_2$.
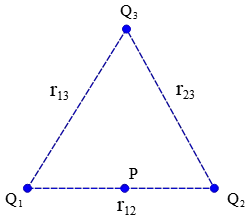
Recall that the electric potential due to a system of point charges at an arbitrary point is defined as $V={\Sigma }^N_{i=1}V_i={\Sigma }^N_{i=1}k\frac{q_i}{r_i}$ . Therefore first find the distance of each point charges to the point P and then find the electric potential.
\[r_3=\sqrt{r^2_{23}-r^2_2}=1.16\ {\rm m}\]
\[r_2=\frac{1}{2}r_{12}=0.67\ {\rm m\ \ ,\ \ }{{\rm r}}_{{\rm 1}}{\rm =}\frac{{\rm 1}}{{\rm 2}}r_{12}=0.67\ {\rm m}\]
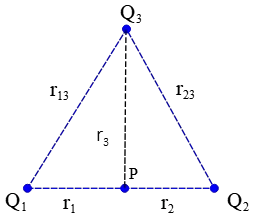
\[V_P=k\left(\frac{Q_1}{r_1}+\frac{Q_2}{r_2}+\frac{Q_3}{r_3}\right)\]
\[=\left(8.99\times {10}^9\right)\left(\frac{6.84\times {10}^{-6}}{0.67}+\frac{\left(-16.2\times {10}^{-6}\right)}{0.67}+\frac{9.20\times {10}^{-6}}{1.16}\right)\]
\[=\left(8.99\times {10}^9\right)\left(-6.04\times {10}^{-6}\right)=-5.43\times {10}^4\ {\rm V}\]
Two protons are near the surface of the earth. The first proton is placed securely on the ground. How high will the second proton have to be placed in order to just remain stationary above the Earth's surface?
Two forces acting on the second proton. One is the Coulomb force due to the first proton and the second is the gravity so these forces must be in balance.
\begin{align*} F_e&=F_g \\ \\\frac{kq_1q_2}{r^2}&=m_2g\\\\ \Rightarrow r&=\sqrt{\frac{kq_1q_2}{m_2g}}\\\\&=\sqrt{\frac{\left(9\times {10}^9\right){\left(1.06\times {10}^{-19}\right)}^2}{\left(1.672\times {10}^{-27}\right)\left(9.8\right)}}\\\\&=0.119\quad{\rm m}\end{align*}
Two equal but oppositely charges spheres ($\pm 5\times {10}^{-8}{\rm C}$) are hanging vertically from $10\,{\rm cm}$ strings. These spheres each have a mass of $2\, {\rm g}$, and are separated by a very thin insulating sheet. At $t=0$, an external electric field is applied horizontally, and the charges separate, coming to equilibrium when an angle of $20{}^\circ $ is between the two strings.
(a) Is the external electric field pointing to the right or to the left?
(b) What is the magnitude of the external electric field?

Note: the force acting on a positive charge due to an electric field is in direction of the field but a negative charge is in opposite direction. So $E$ must be pointed to the left (see the figure).
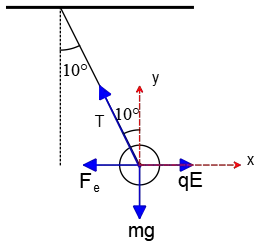
Since the system is in equilibrium so apply the equilibrium conditions to one of the spheres, say the negative sphere, i.e. $\Sigma F_y=0\ ,\ \Sigma F_x=0$
\begin{gather*} \Sigma F_y=T{\cos 10{}^\circ \ }-mg=0\\\\ \Rightarrow T=\frac{mg}{{\cos 10{}^\circ \ }}=\frac{\left(0.002\right)\left(9.8\right)}{{\cos 10{}^\circ \ }}=0.02\, {\rm N} \\ \\ \Sigma F_x=\underbrace{T{\sin 10{}^\circ \ }}_{T_x}+\underbrace{\frac{kq^2}{r^2}}_{F_e}-qE=0\end{gather*} Therefore, \begin{align*}E&=\frac{1}{5\times {10}^{-8}}\left((0.02)(\sin 10^\circ)+\frac{(9\times {10}^9){\left(5\times {10}^{-8}\right)}^2}{(0.03473)^2}\right)\\\\&=4.42\times {10}^5\quad {\rm N/C}\end{align*} Where $r$ is the distance between the charges and is found by Pythagoras theorem as shown in the figure. \begin{gather*} \sin 10^\circ=\frac{\frac{r}{2}}{10}\\\\\Rightarrow r=20\,{\sin 10^\circ}=3.473\quad {\rm cm}\end{gather*}
Consider a sphere with uniform charge density $\rho$ Suppose that at a point ${\mathbf a}$ from the origin a spherical cavity, free of charge is made. The spherical cavity is entirely within the sphere. Calculate the electric field vector inside the cavity (hint: use the concept of superposition).
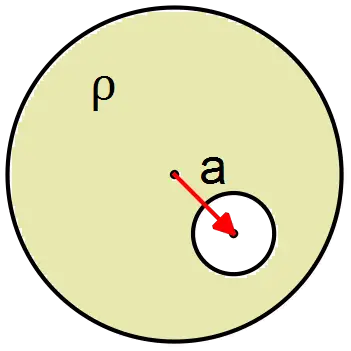
Superposition principle: consider a sphere with charge density $\rho$ and a sphere with 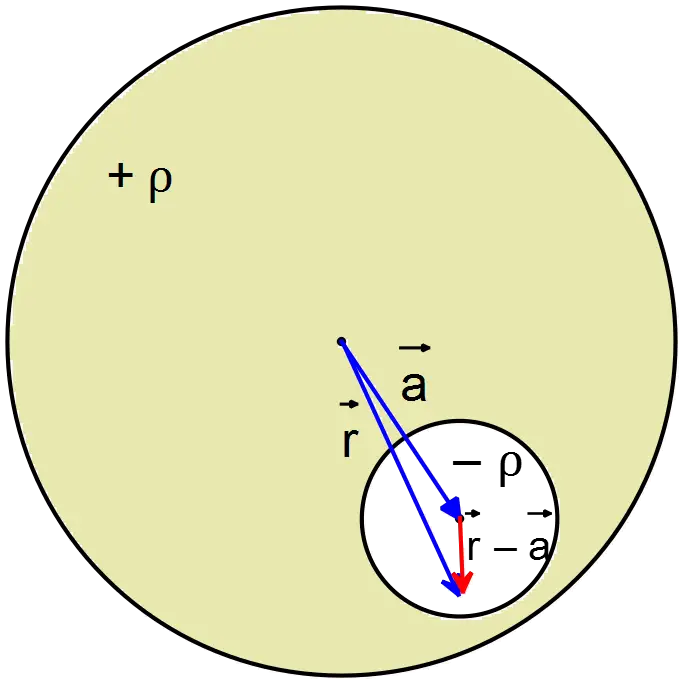 charge density $-\rho$ at point $\vec{a}$ as shown in the figure below. The radius of the sphere with $\rho$ is larger than that of $-\rho$. Now using Gauss's law, we must find the electric field inside a uniform charge density at arbitrary point as
charge density $-\rho$ at point $\vec{a}$ as shown in the figure below. The radius of the sphere with $\rho$ is larger than that of $-\rho$. Now using Gauss's law, we must find the electric field inside a uniform charge density at arbitrary point as
\[\oint_S{\vec{E}.d\vec{S}}=\frac{Q_{enc}}{\epsilon_0}\Rightarrow \vec{E}.\oint_S{d\vec{S}}=\frac{\rho V_{Gaussian}}{\epsilon_0}\]
Where $\oint_S{d\vec{S}}$ is the area of the Gaussian surface with radius $r$ inside of the sphere with radius $R$. So the electric field at distance $r$ from the center of sphere is
\[E\left(4\pi r^2\right)=\frac{\rho\left(\frac{4}{3}\pi r^3\right)}{\epsilon_0}\Rightarrow \vec{E}=\frac{\rho}{3\epsilon_0}\vec{r}\]
In this problem we have two spheres with charge densities $+\rho$ and $-\rho$ . We want to find the electric field due to these charges at point P.
\[{\vec{E}}_{+\rho}(P)=+\frac{\rho}{3\epsilon_0}\vec{r}\]
\[{\vec{E}}_{-\rho}(P)=\frac{-\rho}{3\epsilon_0}(\vec{r}-\vec{a})\]
\[{\vec{E}}_P={\vec{E}}_{+\rho}\left(P\right)+{\vec{E}}_{-\rho}\left(P\right)=+\frac{\rho}{3\epsilon_0}\vec{r}-\frac{\rho}{3\epsilon_0}\left(\vec{r}-\vec{a}\right)\]
\[\Rightarrow {\vec{E}}_P=+\frac{\rho}{3\epsilon_0}\vec{a}\]
If the electric potential in a region is given by $V\left(x\right)=6/x^2$, what is the $x$ component of the electric field in that region?
By definition, $E=-dV(x)/dx\ $, therefore
\[E=-\frac{d}{dx}\left(\frac{6}{x^2}\right)=-\frac{d}{dx}\left(-12x^{-3}\right)=\frac{12}{x^3}\]
A $+4.0\, \mu {\rm C}$ point charge and a $-4.0\, \mu {\rm C}$ point charges are placed as shown in the figure. What is the potential difference $V_A-V_B$ between points A and B?
The potential electric at the distance $r$ from the point charge $q$ is determined by $V\left(r\right)=kq/r$. The potential difference of a collection of point charges at arbitrary point A is found by summing individual potential at that point as $V_A=V_1+V_2+\dots $. Therefore,
\[V_A=V_4+V_{-4}=\frac{kq_1}{r_1}+\frac{kq_2}{r_2}=\left(9\times {10}^9\right)\left\{\frac{4\times {10}^{-6}}{0.3}+\frac{-4\times {10}^{-6}}{\sqrt{{\left(0.4\right)}^2+{\left(0.3\right)}^2}}\right\}=48\ {\rm kV}\]
\[V_B=V_4+V_{-4}=\frac{kq_1}{r_4}+\frac{kq_2}{r_3}=\left(9\times {10}^9\right)\left\{\frac{4\times {10}^{-6}}{0.5}+\frac{-4\times {10}^{-6}}{0.3}\right\}=-48\ {\rm kV}\]
So, $V_A-V_B=48-\left(-48\right)=96\ {\rm kV}$
Find the potential difference $(V_B-V_A)$ between point $A(x=0,y=0)$ and point $B(x=5{\rm m,y=-5m)}$ for an electric field $\vec{E}=500\hat{i}-200\hat{j}\ {\rm (}\frac{{\rm V}}{{\rm m}}{\rm )}$.
By definition, the potential difference between two points A and B are
\[\Delta V=V_B-V_A=-\int^B_A{\vec{E}.d\vec{l}}\]
Since the electric field in this case is uniform so can be factored from the integral as
$\Delta V=-\vec{E}.\int^B_A{d\vec{l}}=-\vec{E}.\Delta \vec{r}$ , where $\Delta \vec{l}$ is the displacement vector between A, B and defined as $\Delta \vec{r}={\vec{r}}_B-{\vec{r}}_A=\left(x_B-x_A\right)\hat{i}+\left(y_B-y_A\right)\hat{j}=5\hat{i}+\left(-5\right)\hat{j}$. Therefore,
\[\Delta V=-\left(500\hat{i}-200\hat{j}\right).\left(5\hat{i}-5\hat{j}\right)=-\left[\left(500\times 5\right)\underbrace{\left(\hat{i}.\hat{i}\right)}_{1}+\left(200\times 5\right)\underbrace{\left(\hat{j}.\hat{j}\right)}_{1}\right]\]
\[\therefore \Delta V=-3500\ {\rm V}\]
A $200\ {\rm m}$ long thin wire carries a line charge density $\lambda=264\ {\rm nC/m}$. find the potential difference between points $5.0\, {\rm m}$ and $6.0\, {\rm m}$ on a perpendicular radius to the axis of the wire, provided the perpendicular radius is not near either end of the wire.
As previous, $\Delta V=V_B-V_A=-\int^B_A{\vec{E}.d\vec{l}}\ $where $d\vec{l}$ is the displacement vector between the points so that in this case $d\vec{l}=dr\ \hat{r}$. By Gauss's theorem, the electric field of an infinitely long thin wire is determine as $\vec{E}=\frac{2k\lambda}{r}\hat{r}$, therefore
\[\Delta V=V_5-V_6=-\int^5_6{\frac{2k\lambda}{r}dr}=-2k\lambda{\left.{\ln r\ }\right|}^5_6=-2k\lambda{\ln \frac{5}{6}\ }\]
\[V_5-V_6=-2\left(9\times {10}^9\right)\left(264\times {10}^{-9}\right){\ln \frac{5}{6}\ }=-0.866\ {\rm V}\]
\[\therefore \ \left|\Delta V\right|=0.866\ {\rm V}\]
Three point charges are fixed in place in the right triangle shown below, in which $q_1=0.71\, \mu {\rm C}$ and $q_2=-0.67\, \mu {\rm C}$. What is the magnitude and direction of the electric force on the $+1.0\, \mu {\rm C\ }$(let's call this $q_3$) charge due to the other two charges?
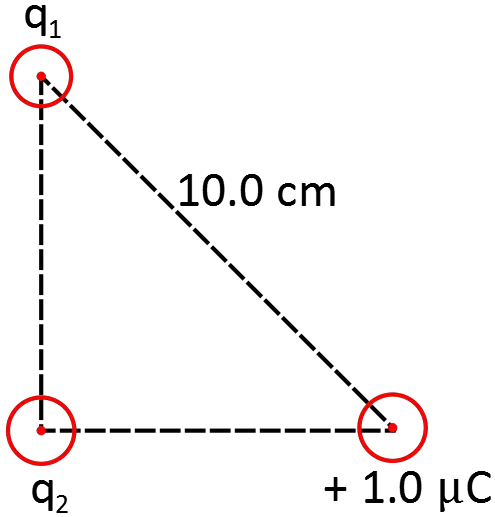
First, find the electric force due to each charge on the $q_3$, then use the superposition principle to do their vector sum.
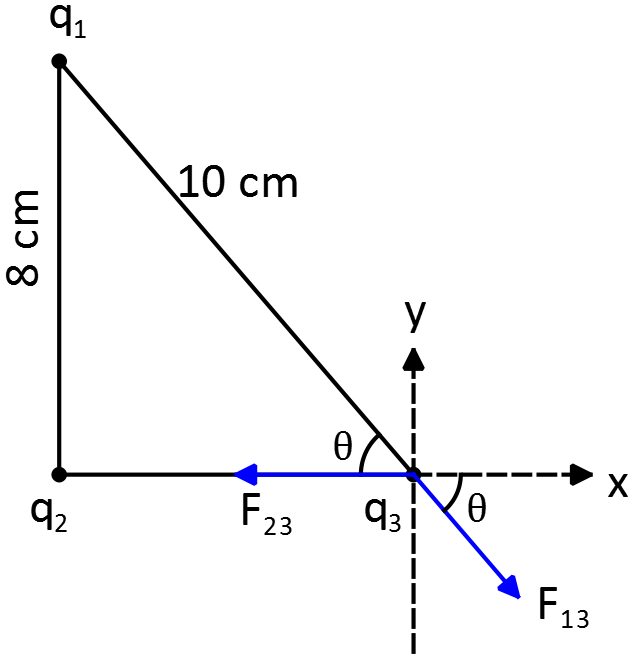
\begin{align*} {\vec{F}}_{13}&=k\frac{\left|q_1\right|\left|q_3\right|}{r^2_{13}}{\hat{r}}_{13}\\&=\left(9\times {10}^9\right)\frac{\left(0.71\times {10}^{-6}\right)\left(1\times {10}^{-6}\right)}{(0.10)^2}\left({\cos \theta}\hat{x}+{\sin \theta}(-\hat{y})\right)\end{align*}
Where we have decomposed the unit vector as above.
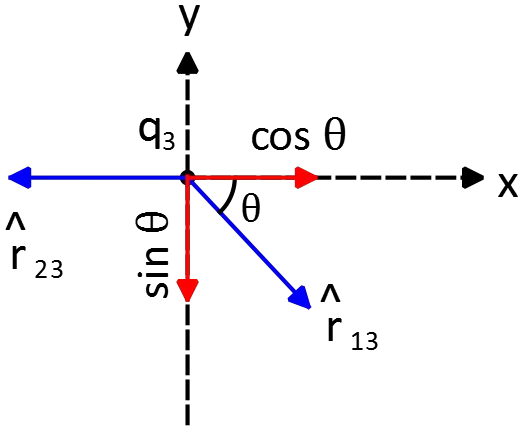
Since $q_1>0$ so the electric field lines are along the line between $q_1$ and $q_3$ and directed away from $q_3$. From the geometry we see that ${\sin \theta\ }=\frac{8}{10}$ and ${\cos \theta\ }=\frac{\sqrt{{10}^2-8^2}}{10}=\frac{6}{10}$. Therefore,
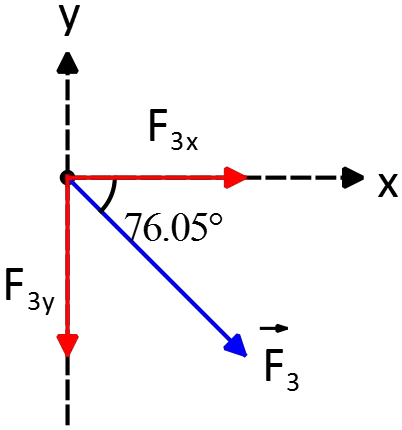
\begin{align*} {\vec{F}}_{13}&=0.639(0.8\,\hat{x}+0.6\,(-\hat{y}))\\&=(0.511\,\hat{x}-0.383\,\hat{y}){\rm \quad N}\end{align*} Now find the electric force due to the $q_2$ on $q_3$ i.e. ${\vec{F}}_{23}$ \begin{align*}{\vec{F}}_{23}&=k\frac{\left|q_2\right|\left|q_3\right|}{r^2_{23}}{\hat{r}}_{23}\\&=\left(9\times {10}^9\right)\frac{\left|-0.67\times {10}^{-6}\right|\left(1\times {10}^{-6}\right)}{\left({10}^2-8^2\right)\times {10}^{-4}}(-\hat{y})\\&=(-1.675\, \hat{y})\quad {\rm N}\end{align*} Therefore, the resultant force on the $q_3$ is \begin{align*}{\vec{F}}_3&={\vec{F}}_{13}+{\vec{F}}_{23}\\\\&=0.511\,\hat{x}-0.383\,\hat{y}+(-1.675\, \hat{y})\\\\&=(0.511\, \hat{x}-2.058\, \hat{y})\quad {\rm N}\end{align*} The direction of the net force with the $x$ axis are determined by ${\tan \alpha}=\left|F_y/F_x\right|$, so \[\alpha=\tan^{-1} \left(\frac{2.058}{0.511}\right)=76.05{}^\circ \]
Since $F_{3x}>0$ and $F_{3y}<0\ $so the net force lies in the fourth quadrant.
And its magnitude is \[|{\vec{F}}_3|=\sqrt{(0.511)^2+(-2.058)^2}=2.12\quad {\rm N}\]
Two small insulating spheres are attached to silk threads and aligned vertically as shown in the figure. These spheres have equal masses of $40\, {\rm g}$, and carry charges $q_1$ and $q_2$ of equal magnitude $2.0\, \mu {\rm C}$ but opposite sign. The spheres 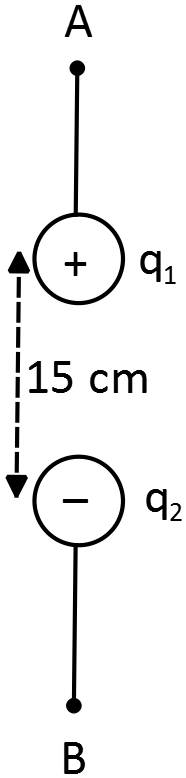 are brought into the positions shown in the figure, with a vertical separation of $15\, {\rm cm}$ between them. Note that you cannot neglect gravity. What is the tension in the lower threads?
are brought into the positions shown in the figure, with a vertical separation of $15\, {\rm cm}$ between them. Note that you cannot neglect gravity. What is the tension in the lower threads?
There is three forces acting on the $q_2$. The electric force due to $q_1$, tension in the thread and the gravity. Thus, its free body diagram is as follows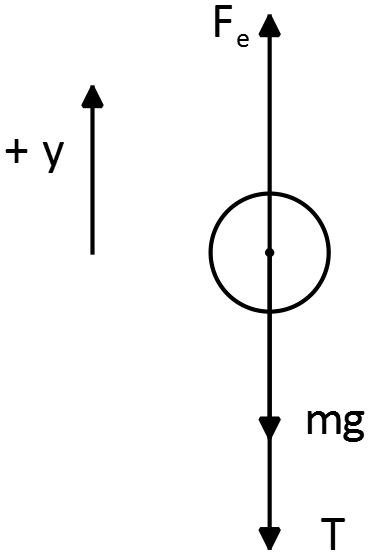
The system is in equilibrium so the net force on the $q_2$ is zero i.e. ${\left(\Sigma F_y\right)}_2=0$
\[\Rightarrow F_e-T-mg=0\ \Rightarrow T=\frac{k\left|q_1\right|\left|q_2\right|}{{\left(15\right)}^2}-mg\]
\[\Rightarrow T=9\times {10}^9\frac{\left(2\times {10}^{-6}\right)\left(2\times {10}^{-6}\right)}{{\left(0.15\right)}^2}-\left(0.040\times 9.8\right)=1.208\ {\rm N}\]
A point charge $Q=-500\ {\rm nC}$ and two unknown point charges $q_1$ and $q_2$ are placed as shown in the figure. The electric field at the origin, due to charges $Q,q_1$ and 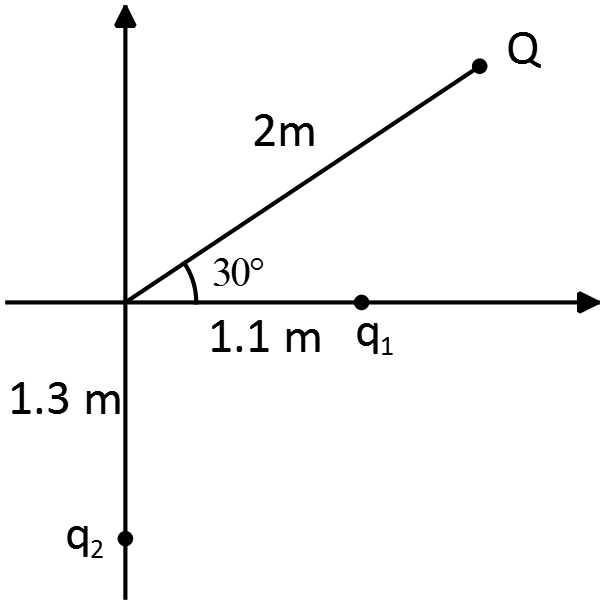 $q_2$ is equal to zero. What is the amount of the charge $q_1$?
$q_2$ is equal to zero. What is the amount of the charge $q_1$?
Because the net electric field at origin is zero, so we have
\[{\vec{E}}_O={\vec{E}}_Q+{\vec{E}}_1+{\vec{E}}_2=0\]
\[\frac{k\left|-Q\right|}{r^2}\hat{r}+\frac{k\left|q_1\right|}{r^2_1}{\hat{r}}_1+\frac{k\left|q_2\right|}{r^2_2}{\hat{r}}_2=0\]
\[\frac{kQ}{2^2}\left({\cos 30{}^\circ \ }\hat{x}+{\sin 30{}^\circ \ }\hat{y}\right)+\frac{k\left|q_1\right|}{{\left(1.1\right)}^2}{\hat{r}}_1+\frac{k\left|q_2\right|}{{\left(1.3\right)}^2}{\hat{r}}_2=0\]
Since $q_1$ and $q_2$ are located in the $x$ and $y$ axis, respectively, so the directions of the electric fields are along theses axes and in opposite direction of the $x$ and $y$ components of the $\vec E_Q$ since the net electric field at origin must be zero. . i.e. ${\vec{E}}_1=\left|E_1\right|\hat{-x}$ and ${\vec{E}}_2=\left|E_2\right|\hat{-y}$. Therefore,
\[\frac{\left(500\times {10}^{-9}\right)}{4}{\cos 30{}^\circ \ }-\frac{\left|q_1\right|}{1.21}=0\Rightarrow \ \left|q_1\right|=1.31\times {10}^{-7}\ {\rm C=131\ nC}\]
\[\frac{\left(500\times {10}^{-9}\right)}{4}{\sin 30{}^\circ \ }-\frac{\left|q_2\right|}{{\left(1.3\right)}^2}=0\Rightarrow \left|q_2\right|=1.05\times {10}^{-7}{\rm C}=105\ {\rm nC}\]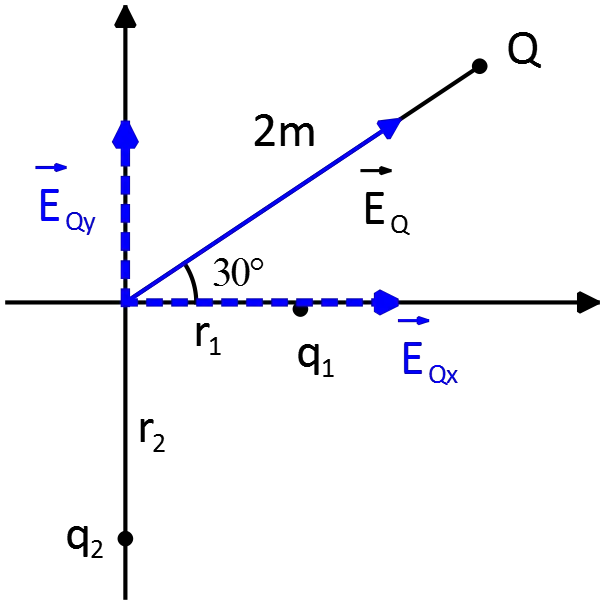
Thus the charge $q_1$ is positive and charge $q_2$ is negative (since the direction of the electric field is toward the charge $q_2$ and away from charge $q_1$ )
The electric field strength in the space between two closely spaced parallel disks is $1.0\times {10}^5\ {\rm N/C}$. This field is the result of transferring $3.9\times {10}^9$ electrons from one disk to the other. What is the diameter of the disks?
This configuration is a parallel plate capacitor. Recall that in this case the electric field between the plates is determined by $E=\sigma {\rm /}\epsilon_0$, where $\sigma$ is the surface charge density of the plates. Therefore,
\[\sigma=\epsilon_0E=\frac{Q}{A_{disk}}\Rightarrow \ \epsilon_0E=\frac{Q}{\pi r^2}\Rightarrow r=\sqrt{\frac{Q}{\pi \epsilon_0E}}\]
\[\Rightarrow r=\sqrt{\frac{ne}{\pi \epsilon_0E}}=\sqrt{\frac{\left(3.9\times {10}^9\right)\left(1.6\times {10}^{-19}\right)}{\pi\left(8.85\times {10}^{-12}\right)\left({10}^5\right)}}=0.015\ {\rm m}\]
In above we have used the relation $Q=ne$, where $n$ is the number of the electrons.
At a distance of $5.8\, {\rm cm}$ from the center of a very long uniformly charged wire, the electric field has magnitude $2000\, {\rm N/C\ }$and is directed toward the wire. What is the charge on a $1.00\, {\rm cm}$ length of wire near the center?
Note: the electric field due to an infinitely long line charge of uniform charge density $\lambda$ at distance $r$ from it is ${\vec{E}}_r=\frac{1}{2\pi\epsilon_0}\frac{\lambda}{r}\hat{r}=2k\frac{\lambda}{r}\hat{r}$. Therefore,
\[\Rightarrow \lambda=\frac{rE}{2k}=\frac{0.058\times 2000}{2\times 9\times {10}^9}=6.44\times {10}^{-9}\frac{{\rm C}}{{\rm m}}\]
By definition, linear charge density is
\[\lambda=\frac{Q}{L}\Rightarrow Q=\lambda L=\left(6.44\times {10}^{-9}\right)\left(0.01\right)=-0.0644\ {\rm nC}\]
Since the fields line are toward the wire so the distributed charge is negative!
In the figure, charge $q_1=+2.5\,{\rm nC}$ is located at the origin, charge $q_2=2.0\,{\rm nC}$ is located on the $x$-axis at $x=+4.0{\rm cm}$, and point P is located at $x=+4.0\,{\rm cm},\ y=+3.0\,{\rm cm}$.
(a) Calculate the magnitude and direction of the electric field at point P.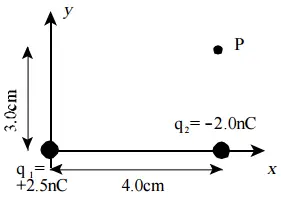
(b) Calculate the electric potential at point P.
(c) A $+2.0\,{\rm nC}$ charge is placed at point P. What is the magnitude of the electric force this charge experiences?
(a) Recall that the electric field of a point charge at distance $r$ is $\vec{E}=k\frac{\left|q\right|}{r^2}\hat{r}$. So first find the electric fields of the charges at P
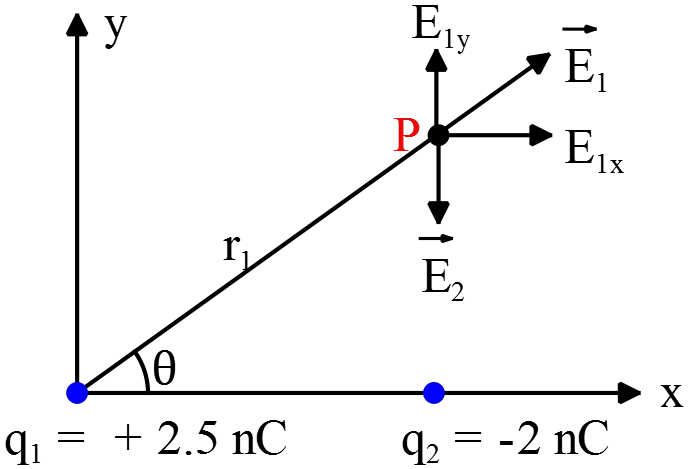
\begin{align*} {\vec{E}}_2&=k\frac{\left|q_2\right|}{r^2_2}{\hat{r}}_2\\&=k\frac{\left|-2\times {10}^{-9}\right|}{{\left(0.03\right)}^2}\left(-\hat{y}\right)\\ &=22.22\times {10}^{-9}k\ (-\hat{y}) \end{align*} Since ${\vec{E}}_2$ is vertical and points in the negative $y$ direction (for negative point charges, the field lines are directed radially inward), we have chosen $(-\hat{y})$.
\begin{align*}{\vec{E}}_1&=k\frac{|q_1|}{r^2_1}{\hat{r}}_1\\\\&=k\frac{2.5\times {10}^{-9}}{(0.04)^2+(0.03)^2}{\hat{r}}_1\\\\&=(10\times {10}^{-9})k({\cos \theta}\,\hat{x}+{\sin \theta}\,\hat{y}) \end{align*} Where we have decomposed the unit vector in the $r_1$ direction. (Since $q_1$ is positive the electric field lines points directly away from the point P and vice versa)
From the geometry \[{\sin \theta\ }=\frac{3}{5}\ \ ,\ {\cos \theta\ }=\frac{4}{5}\ \] To find the total electric field at P combine the results above as\begin{align*}{\vec{E}}_P&={\vec{E}}_1+{\vec{E}}_2\\\\&=(10\times {10}^{-9})k\left(\frac{4}{5}\hat{x}+\frac{3}{5}\ \hat{y}\right)+22.22\times {10}^{-9}k\,(-\hat{y})\\\\&={10}^{-9}k(8\hat{x}-16.22\hat{y})\end{align*}The magnitude of ${\vec{E}}_P$ is as follows \begin{align*}\left|{\vec{E}}_P\right|&=\sqrt{E^2_x+E^2_y}\\\\&=\sqrt{{\left(8\times {10}^{-9}k\right)}^2+{\left(-16.22\times {10}^{-9}k\right)}^2}\\\\&=18.08\times {10}^{-9}k\\\\&=162.58\quad {\rm N/C}\end{align*} Where we have substituted $k=8.99\times {10}^9{\rm \frac{N.m^2}{C^2}}$
(b) The electric potential due to a point charge $q$ at distance $r$ is defined as $V(r)=k\frac{q}{r}$ \begin{gather*} V_1\left(P\right)=k\frac{q_1}{r_1}=k\frac{-2\times {10}^{-9}}{0.03}=-599.3\quad {\rm V}\\\\ V_2(P)=k\frac{q_2}{r_2}=\left(8.99\times {10}^9\right)\frac{2.5\times {10}^{-9}}{0.05}=449.5\quad {\rm V} \\\\ \therefore \quad V_P=V_1+V_2=-149.8\ {\rm V}\end{gather*}
(c) If a charge is located in a uniform electric field $E$, then a force with a magnitude of $F=qE$ exerts on it.
\begin{align*}F_P&=qE_P\\\\&=\left(2\times {10}^{-9}\right)\left(162.58\right)\\\\&=325.16\quad {\rm nN}\end{align*}
An electron was accelerated from rest through a potential difference of $1300\ {\rm V}$. What is its speed?
see the work-energy theorem as $\Delta K=K_f-K_i=W_{net}$, where $W_{net}$ is the net work done on the electron. The electric force acting on the electron in a uniform electric field is $F_e=eE$ and subsequently the work done on it is $W=Fx{\cos \theta\ }=\left(eE\right)x{\cos 180{}^\circ \ }=-eEx$. (Since electron moves in the opposite direction of the field so we have $\theta=180{}^\circ $).
\[K_f-K_i=W_e\Rightarrow \frac{1}{2}mv^2_f-0=-\underbrace{\left(-e\right)}_{{\rm have\ negative\ charge}}Ex=eEx\]
But recall that $\Delta V=Ex$. Therefore,
\[\frac{1}{2}mv^2_f=e\Delta V\Rightarrow v_f=\sqrt{\frac{2e\Delta V}{m}}=\sqrt{\frac{2\left(1.6\times {10}^{-19}{\rm C}\right)\left(1300\right)}{9.10\times {10}^{-31}}}=2.138\times {10}^7\ {\rm m/s}\]
A doubly ionized alpha particle ($q=+2e,\ m=4m_p$) is moving in a uniform parallel electric field in a direction opposite of the electric field. When measurements commence, it has a kinetic energy of $56.4\,{\rm MeV}$ and it continuously decelerate to a stop. If it moves $6620\, {\rm km}$ during this time, what is strength of the electric field?
First solution: use the work-energy theorem
SI unit of energy is Joule so we must first convert initial kinetic energy into Joule
\[56.6\ {\rm MeV}\to {\rm 56.4\times }{{\rm 10}}^{{\rm 6}}\times \left(1.6\times {10}^{-19}\right)=9.035\times {10}^{-12}{\rm J}\]
\[\Delta K=K_2-K_1=W_{net}\]
\begin{align*}
0-K_1=\left(qE\right)x\,{\cos 180{}^\circ \ }\Rightarrow E &=\frac{K_1}{qx}=\frac{9.035\times {10}^{-12}}{2\left(1.6\times {10}^{-19}\right)\left(6620\times {10}^3\right)}\\
&= 4.26\ \frac{{\rm N}}{{\rm C}}
\end{align*}
Second solution: first using $v^2-v^2_0=2a\Delta x$ find the acceleration of the particle, then by the Newton's 2${}^{nd}$ law determine the force exerted on it.
\[K_0=\frac{1}{2}\underbrace{m}_{4m_p}v^2_0\Rightarrow v_0=\sqrt{\frac{2K_0}{4m_p}}=\sqrt{\frac{2\left(9.035\times {10}^{-12}\right)}{6.688\times {10}^{-27}}}=5.198\times {10}^7\frac{{\rm m}}{{\rm s}}\]
\[v^2-v^2_0=2a\Delta x\Rightarrow 0-{\left(5.1987\times {10}^7\right)}^2=2a\left(6620\times {10}^3\right)\Rightarrow a=-2.04\times {10}^8\frac{{\rm m}}{{{\rm s}}^{{\rm 2}}}\]
The minus sign indicates that the object is going to decrease its velocity.
\[F=ma=4m_pa=6.688\times {10}^{-27}\times \left(-2.04\times {10}^8\right)=-1.36\times {10}^{-18}\ {\rm N}\]
By definition, the magnitude of the electric field is
\[E=\frac{\left|F\right|}{q}=\frac{\left|-1.36\times {10}^{-18}\right|}{2(1.6\times {10}^{-19})}=4.26\frac{{\rm N}}{{\rm C}}\]
A particle with unknown mass $m$ and charge $q$ is initially moving at constant velocity $v=4\times {10}^5\ {\rm m/s}$ in a region with zero electric field. It then enters a region where the field is $E=100\ {\rm N/C}$, in the same direction as the particle's motion. The particle travels for a distance of $x=1.2\ {\rm cm}$ before momentarily coming to a stop. What is the particle's charge to mass ratio $q/m$? Be sure to include the sign of the ratio and its units.
When a particle moves in an electric field, experiences a force by the field as $F=qE$. Using the work-energy theorem, we get
\[\Delta K=K_2-K_1=W_{net}\]
\[0-\frac{1}{2}mv^2_0=\left(qE\right)x\,{\cos 180{}^\circ \ }\Rightarrow \frac{q}{m}=\frac{v^2_0}{2Ex}\]
\[\Rightarrow \frac{q}{m}=\frac{{\left(4\times {10}^5\right)}^2}{2\times 100\times 1.2\times {10}^{-2}}=6.67\times {10}^{10}\frac{{\rm C}}{{\rm kg}}\]
Note: since the particle comes to a stop so there is a dissipative force exerted on it that is in opposite direction to the motion of the particle so $W=Fx{\cos 180{}^\circ \ }$.
When a positive charge enters in a region with constant $E$ then it moves in the direction of the field and its velocity increased but a negative charge moves opposite of the field and therefore its velocity decreased until come to a stop. In this problem the charge after entering the field come to a stop so it must be negative charge!
An electron (mass = $9.11\times {10}^{-31}{\rm kg}$) is released from rest in a uniform electric field of magnitude of $5000\ {\rm N/C}$. How long would it take the electron to reach a speed of $100\frac{{\rm m}}{{\rm s}}$?
Given data: $v_0=0\ ,\ E=5000\frac{{\rm N}}{{\rm C}}\ ,\ \ \ v=100\frac{{\rm m}}{{\rm s}}\ ,\ t=?$
From the kinematic relation $v=v_0+at$ we need to find the acceleration of the electron in the electric field to calculate the desired time. By definition, force is related to the electric field via $F=qE$ hence
\[F=qE\Rightarrow ma=qE\Rightarrow a=\frac{qE}{m}\]
Substituting in the above kinematic relation and solving for $t$, gets
\[v=v_0+at=v_0+\left(\frac{q}{m}\right)Et\Rightarrow 100=0+\left(\frac{1.6\times {10}^{-19}}{9.11\times {10}^{-31}}\right)\left(5000\right)t\]
\[\Rightarrow t=1.01\times {10}^{-13}\ {\rm s}\]
A line of positive charge is formed into semicircle of radius $R$. The charge per unit length along the semicircle is described by the expression $\lambda=\lambda_0\,{\cos \theta\ }$. Find: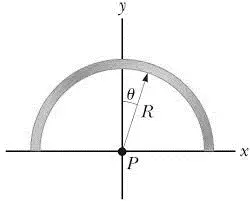
(a) The total charge on the semicircle.
(b) The electric field vector at point P
(a) By definition, the linear charge density of a continuous line is $\lambda=dq/dx$. So
\begin{align*}
dq=\lambda dx\to q_{tot}=\int{\lambda dx}&=2\int^{\frac{\pi}{2}}_0{\lambda_0\,{\cos \theta\ }\left(R\,d\theta\right)}\\
&=2\lambda_0R\,{\left({\sin \theta\ }\right)}^{\frac{\pi}{2}}_0\\
&=2\lambda_0R
\end{align*}
In the above, we have used the symmetry of the problem. 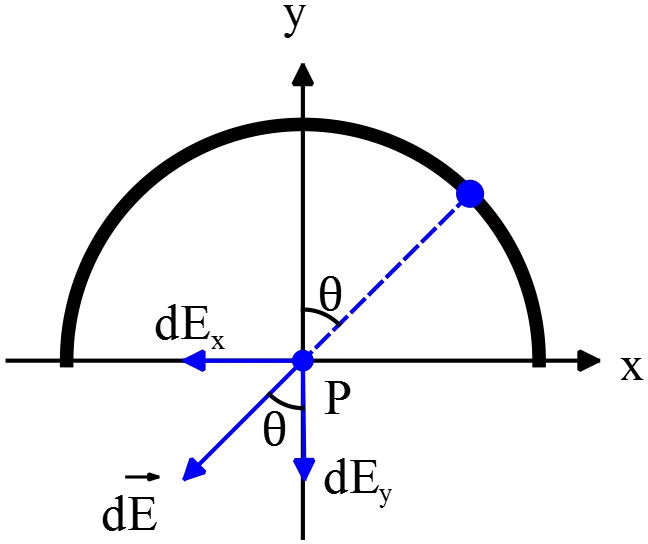
(b) First, determine the electric field due to a charge element at P then integral over it to find the total electric field.
\begin{align*}
{\vec{E}}_P=\int{k\frac{dq}{R^2}\hat{r}}&=\int{k\frac{dq}{R^2}\left({\sin \theta\ }\left(-\hat{x}\right)+{\cos \theta\ }\left(-\hat{y}\right)\right)}\\
&=\underbrace{\int{k\frac{dq}{R^2}{\sin \theta\ }(-\hat{x})}}_{d{\vec{E}}_{Px}}+\underbrace{\int{k\frac{dq}{R^2}{\cos \theta\ }(-\hat{y})}}_{d{\vec{E}}_{Py}}\
\end{align*}
By symmetry, the $x$ component of the electric field becomes zero i.e. $d{\vec{E}}_{Px}=0$. So
\begin{align*}
{\vec{E}}_P&=2\int^{\frac{\pi}{2}}_0{k\frac{dq}{R^2}\,{\cos \theta\ }(-\hat{y})}\\
&=2\frac{k}{R^2}\int^{\frac{\pi}{2}}_0{\lambda ds{\cos \theta\ }\left(-\hat{y}\right)}\\
&=2\frac{k}{R^2}\int^{\frac{\pi}{2}}_0{\left(\lambda_0{\cos \theta\ }\right)(Rd\theta)\,{\cos \theta\ }\left(-\hat{y}\right)}\\
&= \frac{2k\lambda_0}{R}\int^{\frac{\pi}{2}}_0{{{\cos }^{{\rm 2}} \theta\ }d\theta\left(-\hat{y}\right)}\\
& =\frac{2k\lambda_0}{R}\int^{\frac{\pi}{2}}_0{\frac{1+{\cos 2\theta\ }}{2}}=\frac{2k\lambda_0}{R}\frac{1}{2}{\left(\theta+\frac{1}{2}{\sin 2\theta\ }\right)}^{\frac{\pi}{2}}_0\ \\
& =\frac{\pi k \lambda_0}{2R}\left(-\hat{y}\right)
\end{align*}
A uniformly charged insulating rod of length $14\,{\rm cm}$ is bent into the shape of a  semicircle. The rod has a total charge of $-7.5\, \mu{\rm C}$. Find the magnitude and the direction of the electric field at $O$, the center of the semicircle. Calculate the force on a $3\,\mu{\rm C}$ charge placed at the point P.
semicircle. The rod has a total charge of $-7.5\, \mu{\rm C}$. Find the magnitude and the direction of the electric field at $O$, the center of the semicircle. Calculate the force on a $3\,\mu{\rm C}$ charge placed at the point P.
From the geometry below, we have 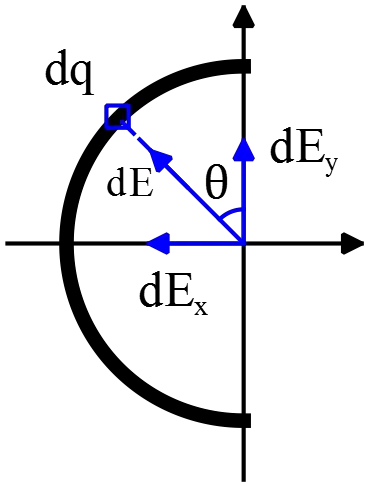
First, calculate the electric field due to an element of charge $dq$ at the point $O$
\[d{\vec{E}}_O=k\frac{dq}{R^2}\hat{r}\xrightarrow{decompose\ \hat r} k\frac{dq}{r^2}\left({\sin \theta\ }\left(-\hat{x}\right)+{\cos \theta\ }\left(\hat{y}\right)\right)\]
By symmetry, we conclude that the $y$ component of the electric field is zero i.e. $d{\vec{E}}_{oy}=0$
So $d{\vec{E}}_O=dE_{ox}=-k\frac{dq}{R^2}{\sin \theta\ }\hat{x}$.
Second, by integration of both sides of the above equation we can get the total electric field at the point P:
\begin{align*}
{\vec{E}}_O=-k\int{\frac{dq}{R^2}{\sin \theta\ }}\hat{x} &=-k\int{\frac{\lambda Rd\theta}{R^2}\,{\sin \theta\ }}\hat{x}\\
&=-\frac{k\lambda}{R}\int^\pi_0{{\sin \theta\ }d\theta}\hat{x}\\
&=-\frac{k\lambda}{R}{\left(-{\cos \theta\ }\right)}^\pi_0\\
&=-\frac{2k\lambda}{R}\hat{x}
\end{align*}
In above we have used the definition of the continuous charge density on a line i.e.
$\lambda=\frac{dq}{dx}$ and the line element in a polar coordinate i.e. 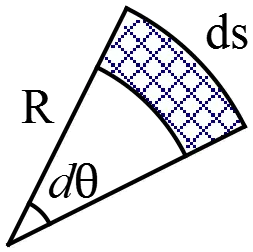 $dx=ds=Rd\theta$.
$dx=ds=Rd\theta$.
Now we can convert $\lambda$ into the explicit charge via $\lambda=\frac{q_{tot}}{L_{semicircle}}=\frac{q_{tot}}{\pi R}$
\begin{align*}
{\vec{E}}_O=-\frac{2k\lambda}{R}\hat{x}&=-\frac{2k\left(\frac{q}{L}\right)}{\frac{L}{\pi}}\hat{x}\\
&=-2k\frac{q\pi}{L^2}\hat{x}\\
&=-2\left(9\times {10}^9\right)\frac{\left(7.5\times {10}^{-6}\right)\pi}{{\left(0.14\right)}^2}\hat{x}\\
&=2.16\times {10}^7\left(-\hat{x}\right)\ \frac{{\rm N}}{{\rm C}}
\end{align*}
Therefore the total electric field at the point P is in the ($-x$) direction.
Finally, by definition of electric field $\vec{E}=\frac{\vec{F}}{q}$ we have
\[F_o=qE_o=\left(3\times {10}^{-6}\right)\left(2.16\times {10}^7\right)\left(-\hat{x}\right)=64.8\ \left(-\hat{x}\right)\ {\rm N}\]
Three charged particles are aligned along the $y$ axis. Find the electric field at $P$ point. 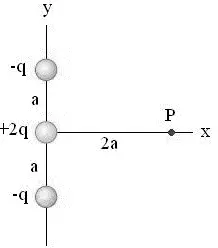 Determine the electric force on a $Q$ charged place on the $P$ point.
Determine the electric force on a $Q$ charged place on the $P$ point.
First, calculate the electric fields due to the point charges at P then apply superposition 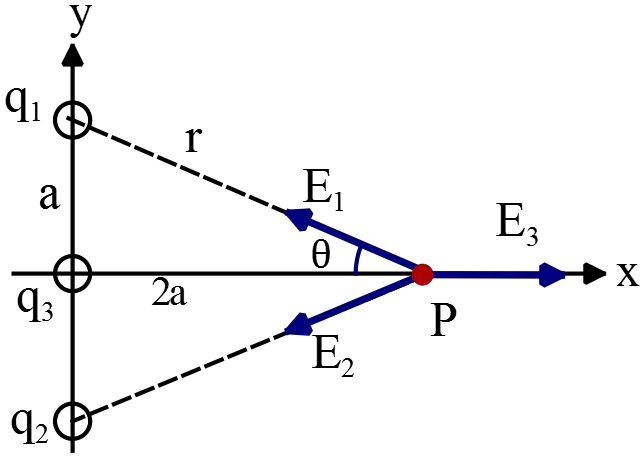 principle: ${\vec{E}}_P={\vec{E}}_1+{\vec{E}}_2+{\vec{E}}_3$ to find the net electric field at that point.
principle: ${\vec{E}}_P={\vec{E}}_1+{\vec{E}}_2+{\vec{E}}_3$ to find the net electric field at that point.
\[\left|E_1\right|=\left|E_2\right|=k\frac{q}{r^2}=k\frac{q}{a^2+{\left(2a\right)}^2}=k\frac{q}{5a^2}\]
\[{\vec{E}}_1=\left|E_1\right|{\hat{r}}_1=k\frac{q}{5a^2}\ {\hat{r}}_1=k\frac{q}{5a^2}\,\left({\cos \theta\ }\left(-\hat{x}\right)+{\sin \theta\ }\left(\hat{y}\right)\right)\]
\[{\vec{E}}_2=\left|E_2\right|{\hat{r}}_2=k\frac{q}{5a^2}{\hat{r}}_2=k\frac{q}{5a^2}\,\left({\cos \theta\ }(-\hat{x})+{\sin \theta\ }\left(-\hat{y}\right)\right)\]
But from the geometry
\[{\cos \theta\ }=\frac{2a}{r}=\frac{2a}{\sqrt{a^2+{\left(2a\right)}^2}}=\frac{2}{\sqrt{5}}\]
\[{\sin \theta\ }=\frac{a}{r}=\frac{a}{\sqrt{a^2+{\left(2a\right)}^2}}=\frac{1}{\sqrt{5}}\]
Therefore
\[{\vec{E}}_1=k\frac{q}{5a^2}\left(-\frac{2}{\sqrt{5}}\hat{x}+\frac{1}{\sqrt{5}}\hat{y}\right)\ \ ,\ \ {\vec{E}}_2=k\frac{q}{5a^2}\left(-\frac{2}{\sqrt{5}}\hat{x}-\frac{1}{\sqrt{5}}\hat{y}\right)\]
On the other hand ${\vec{E}}_3=k\frac{2q}{{\left(2a\right)}^2}=k\frac{q}{2a^2}\hat{x}$
\[\therefore \ {\vec{E}}_P=k\frac{q}{5a^2}\left(-\frac{2}{\sqrt{5}}\hat{x}+\frac{1}{\sqrt{5}}\hat{y}\right)+k\frac{q}{5a^2}\left(-\frac{2}{\sqrt{5}}\hat{x}-\frac{1}{\sqrt{5}}\hat{y}\right)+k\frac{q}{2a^2}\hat{x}=k\frac{q}{a^2}\left(-\frac{4}{\sqrt{5}}+\frac{1}{2}\right) \hat{x}\ {\rm N/C\ }\]
A small $2{\rm g}$ plastic ball is suspended by a $20\ {\rm cm}$ long string in a uniform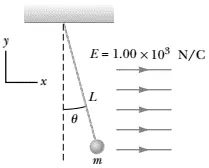 electric field as shown in the figure. If the ball is in equilibrium when the string makes a $15{}^\circ $ angle with the vertical, what is the net charge on the ball?
electric field as shown in the figure. If the ball is in equilibrium when the string makes a $15{}^\circ $ angle with the vertical, what is the net charge on the ball?
The free body diagram below shows the external forces acts on the ball: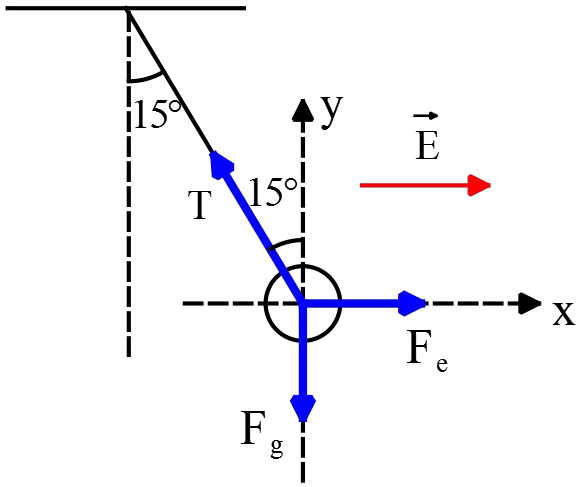
Because the ball is in equilibrium (the ball is motionless) so first write out the equilibrium conditions in $x$ and $y$ directions as follows
\[\Sigma F_x=0=\Sigma F_y\]
\[\Sigma F_y=0\Rightarrow T{\cos \theta\ }-F_g=mg\]
\[\Sigma F_x=0\Rightarrow F_e=T{\sin \theta\ }\]
Dividing both relations by each other, we obtain the angle of the equilibrium position:
\[\therefore {\tan \theta\ }=\frac{{\sin \theta\ }}{{\cos \theta\ }}=\frac{\frac{F_e}{T}}{\frac{mg}{T}}=\frac{F_e}{mg}=\frac{qE}{mg}\]
Solving for $q$, we get
\[q=\frac{mg}{E}{\tan \theta\ }=\frac{0.002\times 9.8}{{10}^3}{\tan 15{}^\circ \ }=5.25\ \mu{\rm C}\]
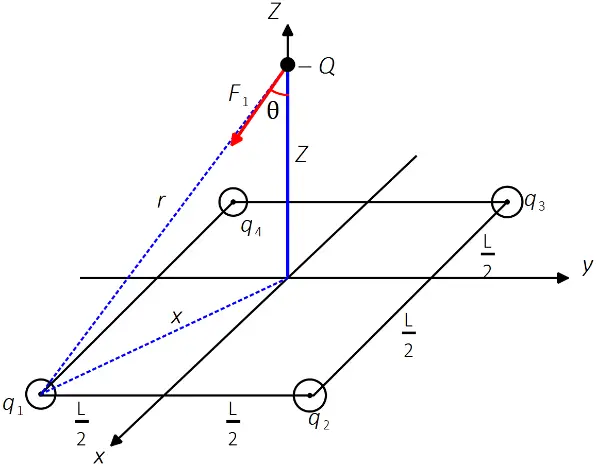
Four identical particles, each having charge $+q$, are fixed at the corners of a square of side $L$. A fifth point charge $-Q$ (at $P$ point) lies a distance $z$ along the line perpendicular to the plane of the square and passing through the center of the square. Determine the force exerted by the other four charges on $-Q$.
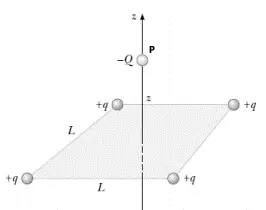
Because the magnitude and distance of all of the charges are equal so
\[\left|F_1\right|=\left|F_2\right|=\left|F_3\right|=\left|F_4\right|=k\frac{\left|qQ\right|}{r^2}\]
By symmetry consideration, $F_x=F_y=0$. So the direction of one of the forces is:
\[{\vec{F}}_{1z}=k\frac{\left|qQ\right|}{r^2}\,{\cos \theta\ }\left(-\hat{k}\right)=-k\frac{\left|qQ\right|}{r^3}z\hat{k}\]
Where we have used from the geometry of the problem ${\cos \theta\ }=z/r$.
By symmetry ${\vec{F}}_{1z}={\vec{F}}_{2z}={\vec{F}}_{3z}={\vec{F}}_{4z}=-k\frac{\left|qQ\right|}{r^3}z\hat{k}$
So
\[{\vec{F}}_z={\Sigma }^4_{i=1}{\vec{F}}_{iz}=-4k\frac{qQ}{r^3}z\hat{k}\]
In terms of the parameters of the square and using the Pythagoras theorem, we have:
\[x=\frac{\sqrt{2}}{2}L\ ,\ r=\sqrt{z^2+{\left(\frac{\sqrt{2}}{2}L\right)}^2}\]
\[{\vec{F}}_z=-4k\frac{Qq}{{\left(z^2+{\left(\frac{\sqrt{2}}{2}L\right)}^2\right)}^{\frac{3}{2}}}z\ \hat{k}\]
Three point charges are located at the corners of an equilateral triangle an in the figure. 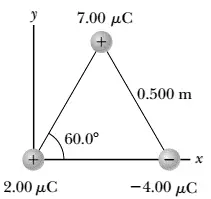 Find the magnitude and direction of the net electric force on the $7\, \mu{\rm C}$ charge.
Find the magnitude and direction of the net electric force on the $7\, \mu{\rm C}$ charge.
Same as previous problem, first we must calculate each of the electric forces due to 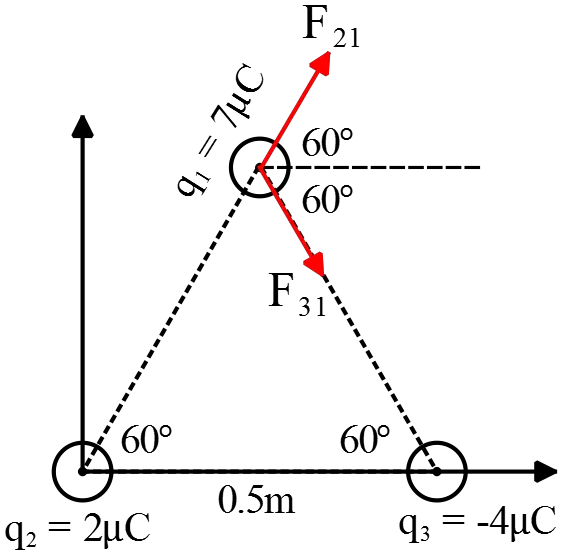 the $2\,\mu{\rm C}$ , $-4\,{\rm C}$ charges exerts on the third charge then use the superposition principle to determine the net electric force on it.
the $2\,\mu{\rm C}$ , $-4\,{\rm C}$ charges exerts on the third charge then use the superposition principle to determine the net electric force on it.
\begin{align*}
{\vec{F}}_{21}&=k\frac{\left|q_1q_2\right|}{r^2_{12}}{\hat{r}}_{21}\\
&=9\times {10}^9\frac{2\times {10}^{-6}\times 7\times {10}^{-6}}{{\left(0.5\right)}^2}{\hat{r}}_{21}\\
&=0.504\ {\hat{r}}_{21}\,{\rm N}
\end{align*}
${\hat{r}}_{21}$ is the unit vector points from $q_2$ toward $q_1$ so if one decomposes it, we get
\[{\vec{F}}_{21}=0.504\left(\frac{1}{2}\hat{x}+\frac{\sqrt{3}}{2}\hat{y}\right){\rm N}\]
(Notation: $F_{12}$ is the force exerted by point charge $q_1$on point charge $q_2$)
\begin{align*}
{\vec{F}}_{31}&=k\frac{\left|q_1q_3\right|}{r^2_{13}}{\hat{r}}_{31}\\
&=9\times {10}^9\frac{\left|7\times {10}^{-6}\times (-4)\times {10}^{-6}\right|}{{\left(0.5\right)}^2}\left({\cos 60{}^\circ \ }\hat{x}+{\sin 60{}^\circ \ }\left(-\hat{y}\right)\right)\ {\rm N}
\end{align*}
\[{\vec{F}}_{31}=1.008\ \left(\frac{1}{2}\hat{x}+\frac{\sqrt{3}}{2}\left(-\hat{y}\right)\right)\ {\rm N}\]
Using superposition principle: ${\vec{{\rm F}}}_{{\rm 1}}{\rm =}{\vec{{\rm F}}}_{{\rm 31}}{\rm +}{\vec{{\rm F}}}_{{\rm 32}}$, we obtain
\begin{align*}
{\vec{{\rm F}}}_{{\rm 1}}&=0.504\left(\frac{1}{2}\hat{x}+\frac{\sqrt{3}}{2}\hat{y}\right)+1.008\ \left(\frac{1}{2}\hat{x}+\frac{\sqrt{3}}{2}\left(-\hat{y}\right)\right)\\
&=0.756\ \hat{x}-0.437\ \hat{y}\ \ ({\rm N)}
\end{align*}
\[\left|{\vec{F}}_1\right|=\sqrt{{\left(0.756\right)}^2+{\left(-0.437\right)}^2}=0.873\,{\rm N}\]
And the direction of the resultant force with the horizontal axis ($x$) is
\[\alpha={{\tan }^{-1} \left(\frac{\left|-0.437\right|}{\left|0.756\right|}\right)\ }=30.02{}^\circ \ \]
Since $F_{1x}>0\ $and $F_{1y}<0$ so the net force lies in the fourth quadrant.
Four point charges are at the corners of a square of side $a$ as in the figure. 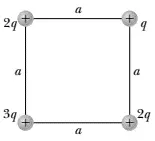
(a) Determine the magnitude and direction of the electric field at the location of charge $q$
(b) What is the resultant force on $q$.
(a) Note: electric field defined as the electric force per unit charge. i.e. $\vec{{\rm E}}=\frac{\vec{{\rm F}}}{q}$. 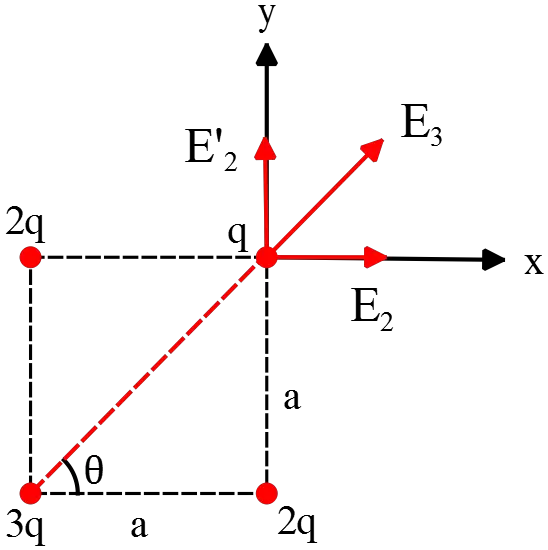
The net electric field of a system of point charges at any point obeys the superposition principle.
At the location of $q$, because of the $+3q$, there is an electric field
\[{\vec{E}}_3=k\frac{3q}{a^2+a^2}\hat{r}=\frac{3}{2}k\frac{q}{a^2}\hat{r}\]
Where we have used the Pythagoras theorem $r^2=a^2+a^2$. $\hat{r}$ is the unit vector points from $3q$ toward $q$ that must be decomposed in $\hat{x}$ and $\hat{y}$ directions, as follows
\[\hat{r}=\hat{x}\,{\cos \theta\ }+\hat{y}\,{\sin \theta\ }\]
So ${\vec{E}}_3=E_{3x}\hat{x}+E_{3y}\hat{y}=\frac{3}{2}k\frac{q}{a^2}\left({\cos \theta\ }\hat{x}+{\sin \theta\ }\hat{y}\right)$ but ${\tan \theta\ }=\frac{a}{a}=1\Rightarrow \theta=45{}^\circ $
The electric fields due to the charges $+2q$ at the $+q$ location are:
\[{\vec{E}}_2=k\frac{2q}{a^2}\ \hat{x}\ \ ,\ \ {\vec{E}}^{'}_2=k\frac{2q}{a^2}\hat{y}\]
Therefore the net electric field of three point charges $+3q,+2q,+2q$ at the location of the fourth charge is (by using the superposition principle):
\begin{align*}
{\vec{E}}_{net}&={\vec{E}}_3+{\vec{E}}_2+{\vec{E}}^{'}_2\\
&=\frac{3}{2}k\frac{q}{a^2}\left({\cos 45{}^\circ \ }\hat{x}+{\sin 45{}^\circ \ }\hat{y}\right)+k\frac{2q}{a^2}\left(\hat{x}+\hat{y}\right)\\
&=k\frac{q}{a^2}\left[\left(\frac{3}{2}{\cos 45{}^\circ \ }+2\right)\hat{x}+\left(\frac{3}{2}{\sin 45{}^\circ \ }+2\right)\hat{y}\right]\\
&=\left(2+\frac{3}{2\sqrt{2}}\right)k\frac{q}{a^2}(\hat{x}+\hat{y})
\end{align*}
But we know that the magnitude and direction of a vector with components $\vec{a}=a_x\hat{x}+a_y\hat{y}$ is
$\left|a\right|=\sqrt{a^2_x+a^2_y}$ and $\alpha={{\tan }^{-1} \left(\frac{\left|a_y\right|}{\left|a_x\right|}\right)\ }$ with positive $x$ axis.
Therefore, the magnitude and direction of the net electric field is
\[\left|{\vec{E}}_{net}\right|=\left(2+\frac{3}{2\sqrt{2}}\right)k\frac{q}{a^2}\ \sqrt{2}=k\frac{q}{a^2}\left(2\sqrt{2}+\frac{3}{2}\right)\ \]
\[\alpha={{\tan }^{-1} 1\ }=45{}^\circ !\]
(b) From the definition of the electric field ${\vec{{\rm F}}}_{{\rm net}}{\rm =}q{\vec{{\rm E}}}_{{\rm net}}$. So
\[{\vec{{\rm F}}}_{{\rm net}}=\left(2+\frac{3}{2\sqrt{2}}\right)k\frac{q^2}{a^2}(\hat{x}+\hat{y})\]
And $\left|{\vec{{\rm F}}}_{{\rm net}}\right|=k\frac{q^2}{a^2}\left(2\sqrt{2}+\frac{3}{2}\right)$
Four point charges are at the corners of a square. The distance from each corner to the  center is $0.3\ {\rm m}$. At the center there is a $-q$ point charges. What is the magnitude of the net force on this charge?
center is $0.3\ {\rm m}$. At the center there is a $-q$ point charges. What is the magnitude of the net force on this charge?
Note: the electric force vector between two point charges located at distance $r$ from each other is $\vec{F}=k\frac{\left|q_1q_2\right|}{r^2}\hat{r}$.
When there is a system of point charges and we want to find the net force on one of the charges, we must use the superposition principle i.e. the vector sum of the individual electric forces on the desired charge: ${\vec{{\rm F}}}_{{\rm net}}{\rm =}{\vec{{\rm F}}}_{{\rm 1}}{\rm +}{\vec{{\rm F}}}_{{\rm 2}}{\rm +}{\vec{{\rm F}}}_{{\rm 3}}+\dots $
So we must vector sum the individual forces of four point charges on the $-q$ in the center.
The drawing below shows the direction of the individual forces.
\[\left|F_1\right|=\left|F_2\right|=k\frac{\left|\left(-q\right)\left(+q\right)\right|}{{\left(0.3\right)}^2}=+\frac{kq^2}{0.09}\]
\[\left|F_3\right|=\left|F_4\right|=k\frac{\left|\left(-q\right)\left(-q\right)\right|}{{\left(0.3\right)}^2}=+k\frac{q^2}{0.09}\]
Because the $F_1,F_2$ and $F_3,F_4$ are separately in opposite directions to each other (i.e. ${\vec{F}}_1=-{\vec{F}}_2$ and ${\vec{F}}_3=-{\vec{F}}_4$) so the net force is
\[{\vec{F}}_{net}={\vec{F}}_1+{\vec{F}}_2+{\vec{F}}_3+{\vec{F}}_4=0\]

A non-uniform, but spherically symmetric, distribution of charge has a charge density of $\rho\left(r\right)=\rho_0\left(1-\frac{r}{R}\right)$ for $(r<R)$ and $\rho\left(r\right)=0$ for $(r>R)$ where $\rho_0=\frac{3Q}{\pi R^3}$ is a positive constant.
(a) Show that the total charge contained in the charge distribution is $Q$
(b) Show that the electric field in the region ($r>R$) is identical to that produced by a point charge $Q$ at $r=0$.
(c) Obtain an expression for the electric field for $r<R$ and graph the magnitude of the $E(r)$ as a function of $r$.
(d) Find the value of $r$ at which the electric field $E(r)$ is a maximum, and find the value of that maximum field.
(a) By definition, the total charge distributed in a region of space is $Q=\int{\rho\left(r\right)dV}$
\begin{align*}
Q_{tot}=\int{\rho\left(r\right)dV} &=\int^R_0{\rho_0\left(1-\frac{r}{R}\right)\ 4\pi r^2dr}\\
&= 4\pi \rho_0{\left(\frac{1}{3}r^3-\frac{r^4}{4R}\right)}^R_0\\
&=\frac{1}{3}\pi \rho_0R^3\\
&=\frac{1}{3}\pi R^3\left(\frac{3Q}{\pi R^3}\right)=Q\\
\ \ \ \Rightarrow Q_{tot}=Q
\end{align*}
(b) Use Gauss's law to find the electric field of a charge distribution inside and outside of the desired volume. The charge configuration has spherical symmetry so by symmetry consideration; the electric field must be radial.
\[\oint{\vec{E}.\hat{n}dA}=\frac{Q_{ins}}{\epsilon_0}\ \ ,\ \ {\rm Gauss}{{\rm s}}^{{\rm '}}{\rm s\ law}\]
Where $Q_{ins}$ is the charge inside of a closed surface.
\[E_r\oint{dA}=\frac{Q_{ins}}{\epsilon_0}\to E_r\left(4\pi r^2\right)=\frac{Q_{ins}}{\epsilon_0}\Rightarrow E_r=\frac{Q_{ins}}{4\pi\epsilon_0r^2}\]
if $r>R$ then $E_r=\frac{Q_{ins}}{4\pi\epsilon_0r^2}$ where $Q_{ins}=\int{\rho\left(r\right)dV}=Q$ because the Gaussian surface encloses the overall sphere. Therefore
\[E_r\left(r>R\right)=\frac{Q}{4\pi\epsilon_0r^2}\ ,\ {\rm that\ is\ similar\ to\ th}{\rm e\ electric\ field\ of\ a\ point\ charge}\]
(c) from part (b) , $E_r=\frac{Q_{ins}}{4\pi\epsilon_0r^2}$ but the amount of enclosed charge in a Gaussian surface inside of the sphere is
\begin{align*}
Q_{ins} &=\int{\rho\left(r\right)dV}\\
&=\int^r_0{\rho_0\left(1-\frac{r}{R}\right)4\pi r^2dr}\\
&=4\pi\epsilon_0{\left(\frac{1}{3}r^3-\frac{r^4}{4R}\right)}^r_0\\
&=4\pi\epsilon_0\left(\frac{1}{3}r^3-\frac{r^4}{4R}\right)
\end{align*}
\[\ \Rightarrow E_r\left(r<R\right)=\frac{\rho_0}{\epsilon_0}\left(\frac{1}{3}r-\frac{r^2}{4R}\right)\]
(d) we must find the maximum value of the electric field inside of the sphere so
\[\frac{d}{dr}E_r\left(r<R\right)=\frac{\rho_0}{\epsilon_0}\left(\frac{1}{3}-\frac{r}{2R}\right)=0\Rightarrow r=\frac{2}{3}R\]
\[E_r\left(r=\frac{2}{3}R\right)=\frac{\rho_0}{\epsilon_0}\left(\frac{2}{9}R-\frac{R}{9}\right)=\frac{\rho_0}{9\epsilon_0}R\]
A non-uniform electric field is given by the expression
\[\vec{E}=ay\hat{x}+bz\hat{y}+cx\hat{z}\]
Where $a,b,c$ are constants, $\hat{x},\hat{y},\hat{z}$ are unit vectors in the $x,y,z$ directions, respectively. Determine the electric flux through a rectangular surface in the $xy$ plane, extending from $x=0$ to $x=w$ and from $y=0$ to $y=h$.
Solution: you can find the solution of this problem here.
The cubical surface of side length $L=12\ {\rm cm}$ is shown in the electric field 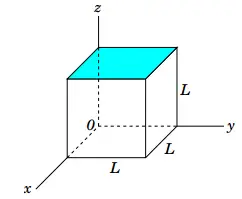 $\vec{E}=\left(950\,y\ \hat{i}+650\,z\hat{k}\right)\ {\rm V/m}$. Find the electric flux through the top face of the cube.
$\vec{E}=\left(950\,y\ \hat{i}+650\,z\hat{k}\right)\ {\rm V/m}$. Find the electric flux through the top face of the cube.
Solution: the solution is here.
An insulating solid sphere of radius $R$ has a uniform positive charge $Q$.
(a) Find charge density $\rho$
(b) Find the electric potential at a point $r$ outside the sphere ($r>R$). Take the potential to be zero at $r=\infty $.
(c) Find the potential at a point inside the sphere ($r<R$)
(d) Plot potential $V(r)$ as a function of the distance from the center.
(e) What can you say about the results (a),(b) and (c) if we have conducting sphere having the same amount of charge on it?
(a) The volume charge density is defined as $\rho=\frac{Q}{V}=\frac{Q}{\frac{4}{3}\pi R^3}\ $.
(b) First from Gauss's law determine the electric field outside the sphere:
\[\oint{\vec{E}.d\vec{A}}=\frac{Q_{en}}{\epsilon_0}\ \ \Longrightarrow \ E_{out}\left(4\pi r^2\right)=\frac{Q}{\epsilon_0}\to E_{out}=\frac{Q}{4\pi\epsilon_0r^2}\ \ like\ a\ point\ charge!\]
Now use the definition of the potential difference as below:
\[V\left(r\right)-V\left(\infty \right)=-\int^r_{\infty }{\vec{E}\left(r\right).d\vec{r}}=-\int^r_{\infty }{\frac{Q}{4\pi \epsilon_0}\frac{dr}{r^2}}\]
\[\therefore V\left(r>R\right)=\ \frac{Q}{4\pi \epsilon_0}\frac{1}{r}\ \ ,\ \ V\left(r=R\right)=\frac{Q}{4\pi \epsilon_0}\frac{1}{R}\]
(c) Similar as previous, use Gauss's law inside the sphere to find the $E_{in}$:
\[\oint{\vec{E}.d\vec{A}}=\frac{Q_{en}}{\epsilon_0}\ \Longrightarrow E\left(r\right)\left(4\pi r^2\right)=\frac{1}{\epsilon_0}\int^r_0{\rho dv}=\frac{1}{\epsilon_0}\rho\left(\frac{4}{3}\pi r^3\right)\ \]
\[\Rightarrow E_{in}\left(r\right)=\frac{\rho}{3\epsilon_0}r\ \ or\ E_{in}\left(r\right)=\frac{Q}{4\pi \epsilon_0R^3}\ r\ \]
\[V\left(r\right)-V\left(R\right)=-\int^r_R{{\vec{E}}_{in}\left(r\right).d\vec{r}}=-\frac{Q}{4\pi \epsilon_0R^3}\ \int^r_R{rdr}=-\frac{Q}{4\pi \epsilon_0R^3}\frac{1}{2}{\left.r^2\right|}^r_R\]
\[V\left(r\right)-\frac{Q}{4\pi \epsilon_0R}=-\frac{Q}{4\pi \epsilon_0R^3}\frac{1}{2}\left(r^2-R^2\right)\ \]
\[\therefore V\left(r<R\right)=\frac{Q}{8\pi\epsilon_0R}\left(3-{\left(\frac{r}{R}\right)}^2\right)\]
(d)
(e)
(i) The charge density inside a conductor is always zero i.e. $\rho_{in}=0$
(ii) $V\left(r>R\right)=\frac{Q}{4\pi \epsilon_0}\frac{1}{r}$
(iii) $V\left(r<R\right)=\frac{Q}{4\pi \epsilon_0}\frac{1}{R}$
An infinitely long non-conducting cylinder of radius $R$ carries a nonuniform volume 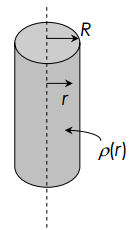 charge density $\rho\left(r\right)=\rho_0\frac{r}{R}$, where $\rho_0$ is known constant and $r$ is the cylindrical radial distance from its axis.
charge density $\rho\left(r\right)=\rho_0\frac{r}{R}$, where $\rho_0$ is known constant and $r$ is the cylindrical radial distance from its axis.
(a) Using Gauss's law determine the electric field vector everywhere (i.e. $r<R$ and $r>R$)
(b) Determine the corresponding electric potential everywhere, choosing $V\left(a\right)=0$, i.e. potential reference chosen at $r=a$ where $a>R$.
(c) Can you choose infinity as potential reference? Give your reasoning.
(a) Due to cylindrical symmetry, the $\vec{E}$ field lines are cylindrically out.
For $r<R$: $\rho_0\int{\vec{E}}.\hat{n}da=Q_{en}=\int^r_0{\rho\left(r^{'}\right)dv}$
\[\epsilon_0E\left(2\pi rL\right)=\int^r_0{\rho_0\frac{r^{'}}{R}\ (r^{'}dr^{'}d\phi dz)}=\frac{\rho_0}{R}\ 2\pi L\frac{r^3}{3}\]
\[\therefore \ \vec{E}\left(r<R\right)=E_{in}=\frac{\rho_0}{3\epsilon_0R}\ r^2\ \hat{r}\]
$\hat{r}$ is the unit vector along the radius and $dv$ is the volume element of the cylinder.
For $r>R$ : $$\epsilon_0\int{\vec{E}}.\hat{n}da=Q_{en}=\int^R_0{\rho\left(r^{'}\right)dv}=2\pi L\frac{\rho_0}{R}\frac{R^3}{3}$$
\[\therefore \ \vec{E}\left(r>R\right)=E_{out}=\frac{\rho_0}{3\epsilon_0r}\ R^2\ \hat{r}\]
(b) The potential difference is defined by $V\left(r\right)-V\left(a\right)=-\int^r_a{\vec{E}.d\vec{l}}$
\[r>R\ :V\left(r\right)=-\int^r_a{\frac{\rho_0}{3\epsilon_0r^{'}}\ R^2}dr^{'}=-\frac{\rho_0R^2}{3\epsilon_0}{\ln \left(\frac{r}{a}\right)\ }\]
\begin{align*}
r<R:\ \ V\left(r\right) &=-\int^r_a{\vec{E}.d\vec{l}}=-\int^R_a{{\vec{E}}_{out}.d\vec{r}}-\int^r_R{{\vec{E}}_{in}.d\vec{r}}\\
&=-\int^R_a{\frac{\rho_0}{3\epsilon_0r}\ R^2dr}-\int^r_R{\frac{\rho_0}{3\epsilon_0R}\ r^2dr}\\
&=-\frac{\rho_0R^2}{3\epsilon_0}{\ln \left(\frac{R}{a}\right)\ }-\frac{\rho_0}{3\epsilon_0R}{\left.\frac{r^3}{3}\right|}^r_R\\
&=-\frac{\rho_0R^2}{3\epsilon_0}{\ln \left(\frac{R}{a}\right)\ }-\frac{\rho_0}{3\epsilon_0R}\frac{1}{3}\ (r^3-R^3)
\end{align*}
(c) Infinity cannot be used as reference point, since the charge distribution extends to $\infty $. You can also this by the problem caused if we set $a\to \infty $.
There is a uniform electric field $\vec{E}=12\frac{V}{m}\ (-\hat{j})$ along the $-y$ axis and these points are given with coordinates $(0,4{\rm m)}$,$B\left(0,0\right),\ C(2{\rm m,0)}$. Find the potential differences: 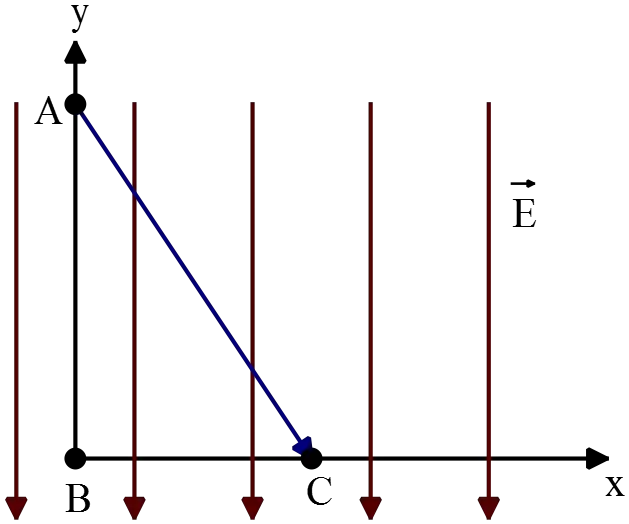
(a) $\Delta V_{AB}$
(b) $\Delta V_{AC}$
(c) If a charge $q_0=0.05\ {\rm C}$ is taken from $A$ to $C$, find the work done on the charge.
(a) The potential difference between two arbitrary points is defined as below
\begin{align*}
\Delta V_{AB}&=-\int^B_A{\vec{E}.d\vec{S}}\\
&= -\int^B_A{12\left(-\hat{j}\right).\left(dx\hat{i}+dy\hat{j}\right)}\\
&=+12\int^B_A{dy}\\
&=+12\int^{y_B}_{y_A}{dy}\\
&=12\int^0_4{dy}\\
&=12{\left(y\right)}^0_4\\
&=12\left(0-4\right)=-48\ {\rm V}
\end{align*}
In above, $d\vec{S}$ is the displacement vector between $A$ and $B$.
(b)
\begin{align*}
\Delta V_{AC}&=-\int^A_C{\vec{E}.d\vec{S}}\\
&=-\int^A_C{12\left(-\hat{j}\right).\left(dx\ \hat{i}+dy\ \hat{j}\right)}\\
&=12\int^{y_B}_{y_A}{dy}\\
&=12\int^0_4{dy}=-48\ {\rm V}
\end{align*}
\[\Delta V_{AB}=\Delta V_{AC}\]
(c) The work done on a charge $q$ in an electric field is $W=q\Delta V$. Therefore,
\[W=q\Delta V=\left(0.05\right)\left(-48\right)=-2.4\ {\rm J}\]
The minus sign indicates that we must does external work to displace $q$ from $A$ to $C$.
The charge $q_1=-5\, \mu{\rm C}$ and $q_2=10\, \mu {\rm C}$ are located as in the 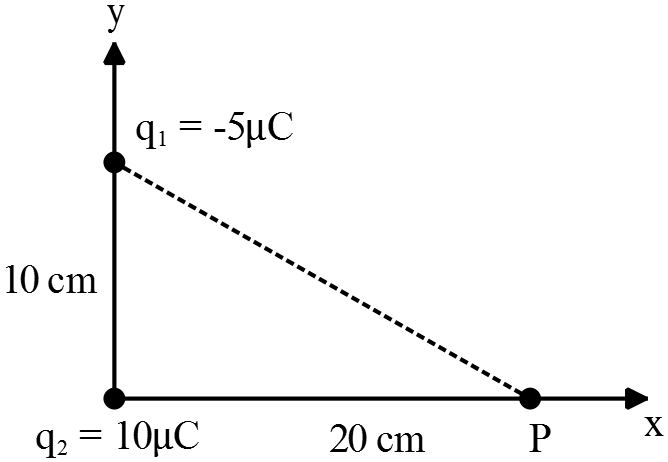 figure.
figure.
(a) Find the electric field due to $q_1$ at the point $P$ located at $20\ {\rm cm}$ along $x$ axis.
(b) Find the electric field of $q_2$ at $P$
(c) What is the total electric field at $P$?
(d) If an electron ($q_e=-1.6\times {10}^{-19}\,C$) is put at $P$ what will be the magnitude of the electric force acting on the electron
Suppose $k=\frac{1}{4\pi \epsilon_0}=9\times {10}^9\ {\rm N.}{{\rm m}}^{{\rm 2}}{\rm /}{{\rm C}}^{{\rm 2}}$
(a) Use the definition of the electric field of a point charge to calculate its magnitude and direction at arbitrary distance.
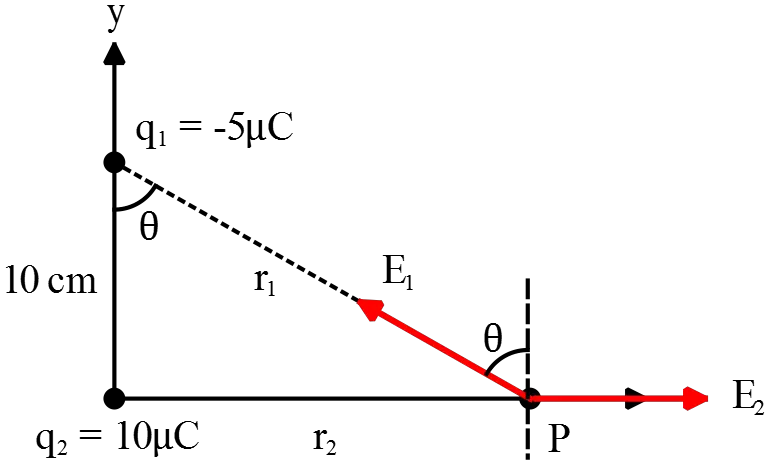 \begin{align*}
\begin{align*}
\vec{E_1}&=k\frac{\left|q_1\right|}{r^2_1}\ {\hat{r}}_1\\
&=k\frac{\left|q_1\right|}{r^2_1}\ \left(\hat{j}\,{\cos \theta\ }-\hat{i}\,{\sin \theta\ }\right)\\
&=k\frac{\left|q_1\right|}{r^2_1}\ \left(\hat{j}\frac{1}{\sqrt{5}}-\hat{i}\frac{2}{\sqrt{5}}\right)\\
&=9\times {10}^9\frac{5\times {10}^{-6}}{0.05}\ \left(\hat{j}\frac{1}{\sqrt{5}}-\hat{i}\frac{2}{\sqrt{5}}\right)
\end{align*}
So $\vec{E_1}=9\times {10}^5\left(\hat{j}\frac{1}{\sqrt{5}}-\hat{i}\frac{2}{\sqrt{5}}\right)=\left(+402.49\ \hat{j}-804.98\hat{i}\right)\times {10}^3\ \left(\frac{{\rm N}}{{\rm C}}\right)$
In above, from the geometry, we have
\begin{gather*}
{\cos \theta\ }=\frac{10}{r_1}=\frac{10}{\sqrt{{10}^2+{20}^2}}=\frac{1}{\sqrt{5}}\\
{\sin \theta\ }=\frac{20}{r_1}=\frac{2}{\sqrt{5}}\\
r^2_1={\left(0.1\right)}^2+{\left(0.20\right)}^2=0.05
\end{gather*}
(b) Similar as part (a),
\begin{align*}
\vec{E_2}&=k\frac{\left|q_2\right|}{r^2_2}{\hat{r}}_2\\
&=9\times {10}^9\frac{\left(10\times {10}^{-6}\right)}{{\left(0.2\right)}^2}\hat{i}\\
&=2250\times {10}^3\hat{i}
\end{align*}
(c) Using the superposition principle, the vector sum of each of the electric fields at arbitrary point $P$ is the total electric field at that point, we obtain
\[\vec{E_P}=\vec{E_1}+\vec{E_2}=\left(1445.02\hat{i}+402.49\hat{j}\right)\times {10}^3\ {\rm N/C}\]
(d) Using the definition of electric field in general, we obtain
\begin{align*}
\vec{F_e}=e\vec{E_e}\ \Rightarrow \ \left|\vec{F_e}\right|&=\left|e\right|\left|\vec{E_P}\right|\\
&=(1.6\times {10}^{-19})\times {10}^3\sqrt{{\left(1445.02\right)}^2+{\left(402.49\right)}^2}\ {\rm N}
\end{align*}
\[\left|\vec{F_e}\right|{\rm \ \sim 2.4\times }{{\rm 10}}^{{\rm -}{\rm 13}}{\rm N}\]
Three different point charges are arranged at the corners of a square of side $L$ shown in 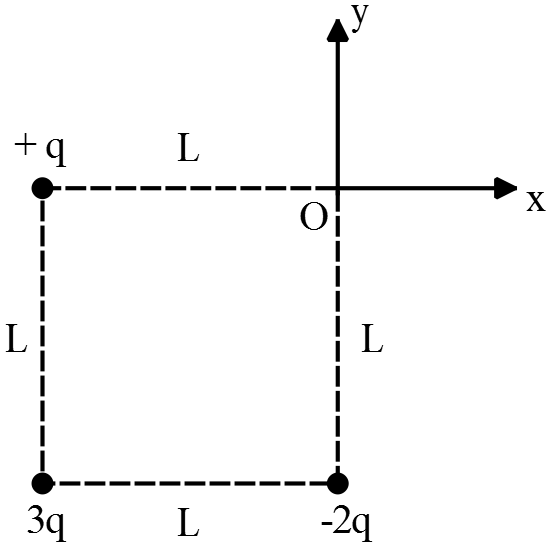 the figure.
the figure.
(a) What is the potential at the forth corner(taken as the origin, point $O$)
(b) What is the electric field vector at point $O$? (Do not forget the unit vectors, simplify your expressions)
(a) The potential electric due to a point charge at distance $r$ is defined by: $V\left(r\right)=\frac{q}{4\pi \epsilon_0r}$. When there is a system of point charges, the potential electric of this system at an arbitrary point P is defined by the sum of each of the potential electric at that point. Therefore,
\[V\left(O\right)=V_q+V_{-2q}+V_{3q}\]
\[V\left(O\right)=\frac{q}{4\pi \epsilon_0}\left[\frac{1}{L}-\frac{2}{L}+\frac{3}{\sqrt{L^2+L^2}}\right]=\frac{q}{4\pi \epsilon_0L}\frac{3\sqrt{2}-2}{2}\ \]
(b) The electric field of a system of point charges is the vector sum of each of the electric fields at that point (superposition Principle).
\[\vec{E}\left(O\right)={\vec{E}}_q+{\vec{E}}_{-2q}+{\vec{E}}_{3q}\]
Note: the electric field of a point charge at distance $r$ is calculated by
\[\vec{E}\left(r\right)=\frac{1}{4\pi \epsilon_0}\frac{\left|q\right|}{r^2}\hat{r}\]
Where $\hat{r}$ is the unit vector along the line from the point charge toward the desired location $r$.
\[\vec{E}\left(O\right)=\frac{1}{4\pi \epsilon_0}\left[\frac{q}{L^2}\hat{i}-\frac{2q}{L^2}\hat{j}+\frac{3q}{2L^2}\frac{\hat{i}+\hat{j}}{\sqrt{2}}\right]=\frac{q}{4\pi \epsilon_0L^2}\left[\hat{i}\frac{4+3\sqrt{2}}{4}-\hat{j}\frac{8-3\sqrt{2}}{4}\right]\]
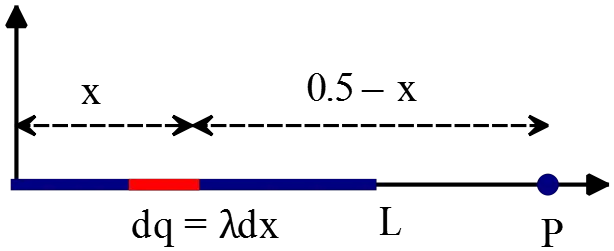
In the figure below, the thin straight wire of length $L$ has a uniformly distributed charge of $Q=+3.0\ {\rm nC}$. Its electric field at point $P$ has magnitude $E=300\ {\rm N/C}$. Find $L$.

First find the total electric field of the wire at point $P$ in terms of $Q$ and $L$. To do this, choose a charge element $dq=\lambda dx$ at distance $x$ from the origin. This element is similar to the point charge, thus one can use the electric field definition and find its magnitude at point $P$( see the figure), then integrate over all of the wire to compute the total field at that point as follows:
\begin{align*}
E=\int{dE}&=\int{\frac{kdq}{{\left(0.5-x\right)}^2}}\\
&=k\lambda\int^L_0{\frac{dx}{{\left(0.5-x\right)}^2}}\\
&=k\lambda{\left(\frac{1}{0.5-x}\right)}^L_0\\
&=k\lambda\left(\frac{1}{0.5-L}-\frac{1}{0.5}\right)\\
&=k\lambda\frac{L}{0.5(0.5-L)}
\end{align*}
Recall that the total charge of the wire is $Q=\lambda L$ so
\[E=\frac{kQ}{0.5(0.5-L)}\]
Now substitute the given values of $E=300\ {\rm N/C}$ and $Q=+3\ {\rm nC}$, solving for $L$, we obtain
\[E=\frac{kQ}{0.5\left(0.5-L\right)}\Rightarrow 300=\frac{\left(9\times {10}^9\right)\left(3\times {10}^{-9}\right)}{0.5\left(0.5-L\right)}\ \]
\[\Rightarrow L=0.32\ {\rm m}\]
A uniformly charged thin ring has radius $a=16.0\, {\rm cm}$ and total charge $Q=+24\, \mu {\rm C}$. Where must a point charge $q=-18\, \mu {\rm C}$ be placed on the axis of the ring for the electric potential at the center of the ring to be zero?
 The electric potential of a point charge at distance $r$ is given by $V\left(r\right)=kq/r$. In the case of continuous charges, we must firstly find the electric potential due to an infinitesimal charge element at distance $r$, then integrate over all of the charge configuration. Thus first calculate the electric potential of a uniformly charged ring at distance $z$ on the axis of the ring
The electric potential of a point charge at distance $r$ is given by $V\left(r\right)=kq/r$. In the case of continuous charges, we must firstly find the electric potential due to an infinitesimal charge element at distance $r$, then integrate over all of the charge configuration. Thus first calculate the electric potential of a uniformly charged ring at distance $z$ on the axis of the ring
\begin{align*}
V=\int{dV}&=\int{\frac{kdq}{r}}\\
&=k\int^{2\pi}_0{\frac{\lambda\,ad\phi}{\sqrt{a^2+z^2}}}\\
&=\frac{k\lambda a}{\sqrt{a^2+z^2}}(2\pi)
\end{align*}
Since we are asked that the electric potential must be computed at the center of the ring so setting $z=0$ we get
\[V_{ring}\left(center\right)=\frac{kQ}{a}\]
As we see, this electric potential at center of the ring is similar to electric potential of a point charge! We have calculated the total charge of the ring as $Q_{ring}=\lambda L=\left(2\pi a\right)\lambda$, where $L$ is the circumference of the ring.
Let $d$ be the distance of point charge $q$ from the center of the ring, so its electric potential at the center of the ring is
\[V_{point}=\frac{kq}{d}\]
The electric potential due to a system of point charges is the sum of the potentials due to each of these charges. Thus the total potential of this configuration at the center of the ring is
\[V=\Sigma V_i=V_{point}+V_{ring}=\frac{kq}{d}+\frac{kQ}{a}\]
Setting $V_{tot}=0$, we obtain
\[0=\frac{kq}{d}+\frac{kQ}{a}\Rightarrow d=-a\frac{q}{Q}=-16\left(-\frac{18}{24}\right)=12\ {\rm cm}\]
A proton moves directly towards a stationary nucleus of charge $Q$. The proton has a speed of $4.15\times {10}^6\ {\rm m/s}$ and an acceleration of $4.31\times {10}^{26}\ {\rm m/}{{\rm s}}^{{\rm 2}}$ when it is $8.00\times {10}^{-14}\ {\rm m}$ from the center of the nucleus. What is the distance of the closest approach (to the center of the nucleus)? Mass of proton $m_{+e}=1.67\times {10}^{-27}{\rm kg}$ , $e=1.6\times {10}^{-19}{\rm C}$
First compute the force between these two point charges at the distance stated in the problem as follows
\[F=\frac{k\left|+eQ\right|}{r^2}\]
Now using Newton's second law and solving for $Q$, we obtain
\[F=ma{\rm =}\frac{k\left|+eQ\right|}{r^2}\Rightarrow \left|Q\right|=\frac{mar^2}{k(+e)}\]
By substituting the given values of the problem, one can find the value of charge $Q$, thus
\[\left|Q\right|=\frac{\left(1.67\times {10}^{-27}\right)\left(4.31\times {10}^{26}\right){\left(8\times {10}^{-14}\right)}^2}{\left(9\times {10}^9\right)\left(1.6\times {10}^{-19}\right)}=3.06\times {10}^{-18}{\rm C}\]
Let $d$ be the closest distance to the center of the nucleus, at this point proton coming to a stop that is its kinetic energy becomes zero so use conservation of mechanical energy between these points to find the desired distance.
\[E_i=E_f\]
\[\underbrace{\frac{k(+e)Q}{r}}_{U_i}+\underbrace{\frac{1}{2}mv^2_i}_{K_i}=\underbrace{\frac{k(+e)Q}{d}}_{U_f}+\underbrace{\frac{1}{2}mv^2_f}_{K_f=0}\]
Rearranging and solving for $d$, we obtain
\[d=\frac{k(+e)Q}{\frac{1}{2}mv^2_i-\frac{keQ}{r}}\]
\[\Rightarrow d=\frac{\left(9\times {10}^9\right)\left(1.67\times {10}^{-19}\right)\left(3.06\times {10}^{-18}\right)}{\frac{1}{2}\left(1.67\times {10}^{-27}\right)\left(4.15\times {10}^6\right)-\frac{\left(9\times {10}^9\right)\left(1.67\times {10}^{-19}\right)\left(3.06\times {10}^{-18}\right)}{8.00\times {10}^{-14}}}\]
\[\Rightarrow d\sim \ 6.4\times {10}^{-14}\ {\rm m}\]
Note: the electric potential energy of a point charge $q$ that is located at distance $r$ from an another charge $Q$ is given by $U=kqQ/r$.
A charge $q$ is distributed uniformly on a quarter side circle of radius $R$ as shown in the 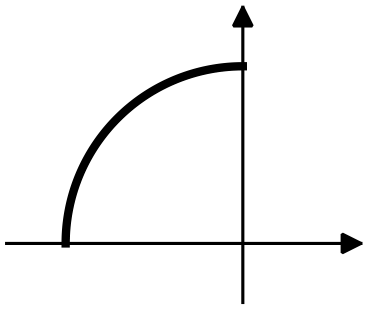 figure. What is the magnitude of the electric field at the center(the point $P$)?
figure. What is the magnitude of the electric field at the center(the point $P$)?
First calculate the electric field of an infinitesimal element of the line at the point $P$, 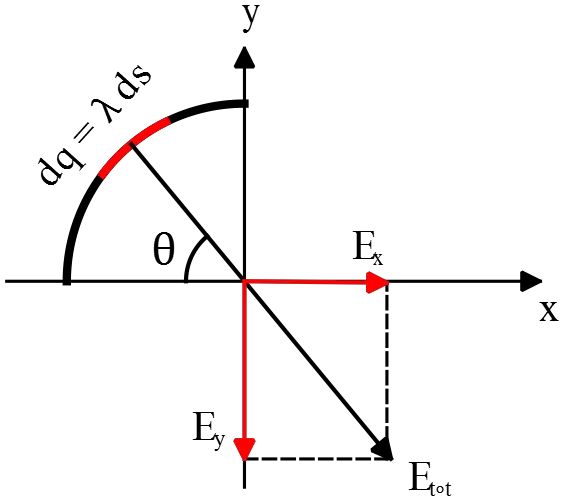 then by integrating over all of the length find the total electric field of the arc at $P$. Thus
then by integrating over all of the length find the total electric field of the arc at $P$. Thus
\[{\vec{E}}_{tot}=\int{d\vec{E}}=\int{\frac{kdq}{R^2}\hat{r}}=\frac{k\lambda R}{R^2}\int{d\theta\ \hat{r}}\]
Recall that the uniformly charge distribution and line element is related together by $dq=\lambda dl$, where in the case of arc $dl=ds=Rd\theta$. $\hat{r}$ is the unit vector along the direction of the total electric field and must be decomposed into $\hat{i}$ and $\hat{j}$. Therefore,
\begin{align*}
{\vec{E}}_{tot}&=\frac{k\lambda}{R}\int^{\frac{\pi}{2}}_0{\left({\cos \theta\ }\,\hat{i}+{\sin \theta\ }\,\left(-\hat{j}\right)\right)d\theta}\\
&=\frac{k\lambda}{R}{\left({\sin \theta\ }\,\hat{i}+{\cos \theta\ }\,\hat{j}\right)}^{\frac{\pi}{2}}_0\\
&=\frac{k\lambda}{R}\left(\hat{i}-\hat{j}\right)
\end{align*}
This is the total electric field at point $P$. Its direction is explicitly shown in the equation and figure. Before finding the magnitude of it, we must explicitly express the total electric field in terms of the charge $q$ of the arc. By using the definition of the linear charge density $\lambda$, we get
\[\lambda=\frac{q}{L}=\frac{q}{R\left(\frac{\pi}{2}\right)}\]
Where, in this case, $L$ is the circumference of the arc. Thus, substituting the $\lambda$ into ${\vec{E}}_{tot}$, we obtain
\[{\vec{E}}_{tot}=\frac{k}{R}\frac{q}{R\left(\frac{p}{2}\right)}\left(\hat{i}-\hat{j}\right)\to {\vec{E}}_{tot}=\frac{2kq}{\pi R^2}\left(\hat{i}-\hat{j}\right)\]
The magnitude of the total electric field is computed as follows
\[\left|{\vec{E}}_{tot}\right|=\sqrt{E^2_x+E^2_y}=\frac{2\sqrt{2}}{\pi}\frac{kq}{R^2}\ \]
And its direction is
\[\theta={{\tan }^{-1} \left|\frac{E_y}{E_x}\right|\ }={{\tan }^{-1} \left|\frac{1}{-1}\right|\ }=45{}^\circ \]
Since $E_x>0\ $and $E_y<0$, then the total electric field lie in the 4${}^{th}$ quadrant.
Two concentric rings, one of radius $R$ and total charge $Q$ and the second of radius 2R 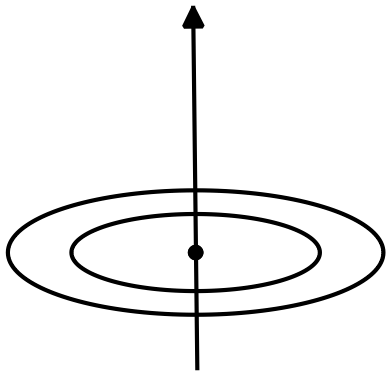 and total charge $-\sqrt{8}Q$, are in the plane $z\ =\ 0$. The charge on each ring is distributed uniformly. Where on the positive $z$-axis is the electric field zero?
and total charge $-\sqrt{8}Q$, are in the plane $z\ =\ 0$. The charge on each ring is distributed uniformly. Where on the positive $z$-axis is the electric field zero?
Calculate the electric field of the rings at distance $d$ on the $z$ axis then use the 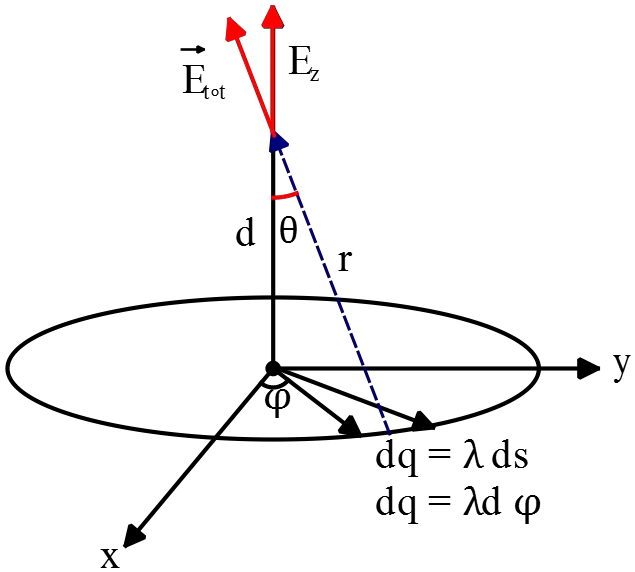 superposition principle to find the total electric field at that point.
superposition principle to find the total electric field at that point.
Choose the $z$ axis to coincide with the axis of the ring with the ring in the $z=0$ plane. The electric field of a ring at a point on its axis through the center of the ring is calculated as follows
\[{\vec{E}}_z=\int{dE_z}=\int{\frac{k\overbrace{dq}^{\lambda Rd\phi }}{r^2}{\cos \theta\ }\hat{k}}=k\lambda R\int^{2\pi}_0{\frac{{\cos \theta\ }}{r^2}d\phi}\]
Where $ds=Rd\phi$ is the length of the arc in the polar coordinate. By symmetry consideration, the $x$ and $y$ components of the electric field due to an element of charge $dq$ is nonzero i.e. $E_x=E_y=0$. As can be seen from the geometry
\[{\cos \theta\ }=\frac{d}{r}\ \ and \ \ r=\sqrt{R^2+d^2}\]
Therefore,
\begin{align*}
{\vec{E}}_z=\int{dE_z}&=\int^{2\pi}_0{\frac{k\lambda R}{r^2}\frac{d}{r}\ d\phi\ \hat{k}}\\
&=\frac{k\lambda Rd}{{\left(R^2+d^2\right)}^{\frac{3}{2}}}\underbrace{\int^{2\pi}_0{d\phi}}_{2\pi}\\
&=\frac{kQd}{{\left(R^2+d^2\right)}^{\frac{3}{2}}}\hat{k}
\end{align*}
Where we have used the definition of the linear charge density on the ring
\[\lambda=\frac{Q}{L}=\frac{Q}{2\pi R}\]
Where $L$ is the circumference of the ring.
Now using the superposition principle and setting ${\vec{E}}_{tot}=0$ and solving for $d$, we obtain the desired location
\[{\vec{E}}_{tot}={\vec{E}}_R+{\vec{E}}_{2R}=\frac{kQd}{{\left(R^2+d^2\right)}^{\frac{3}{2}}}\hat{k}+\frac{k(-\sqrt{8}Q)d}{{\left({\left(2R\right)}^2+d^2\right)}^{\frac{3}{2}}}\hat{k}=0\]
\[\Rightarrow {\left(4R^2+d^2\right)}^{\frac{3}{2}}=\underbrace{\sqrt{8}}_{2^{\frac{3}{2}}}{\left(R^2+d^2\right)}^{\frac{3}{2}}\to {\left(4R^2+d^2-2\left(R^2+d^2\right)\right)}^{\frac{3}{2}}=0\]
The argument of the equation above must be zero to satisfy the condition, thus
\[4R^2+d^2-2\left(R^2+d^2\right)=0\Rightarrow 2R^2-d^2=0\]
\[\therefore d=\sqrt{2}R\]
A hemispherical shell of radius $R$ is placed in an electric field $\vec{E}$ which is parallel 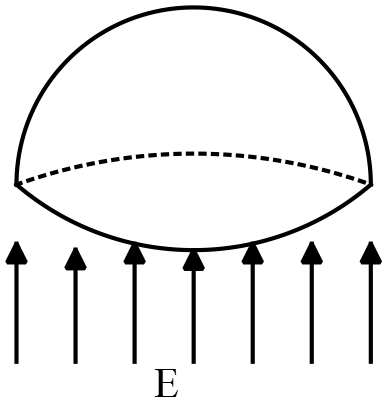 to its axis. What is the flux ${\Phi }_E$ of the electric field through the shell?
to its axis. What is the flux ${\Phi }_E$ of the electric field through the shell?
Solution 1: By definition, the electric flux passing through any surface with area elemen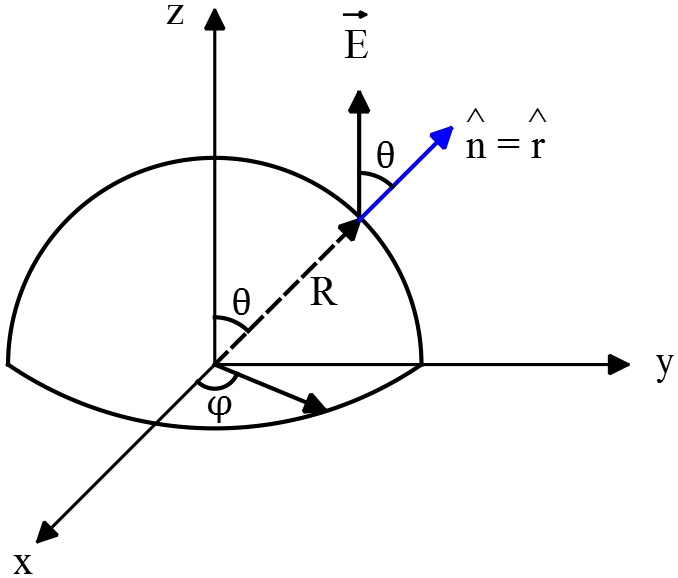 t $dA$ is the scalar product of the normal component of the electric field and area of the surface that is
t $dA$ is the scalar product of the normal component of the electric field and area of the surface that is
\[{\Phi }_E=\int{\vec{E}.\hat{n}dA}\]
Where $\hat{n}$ is the unit vector normal to the surface.
In the case of hemisphere or sphere the unit vector is along the radius i.e. $\hat{n}=\hat{r}$. Since $\vec{E}$ is parallel to the axis of hemisphere the scalar product of $E$ and $\hat{r}$ is $E{\cos \theta\ }$. The range of polar angle is $\theta=0$ to $\theta=\pi/2\ $.Therefore,
\begin{align*} {\Phi }_E=\int^{\frac{\pi}{2}}_0{\vec{E}.\hat{r}dA} &= \int^{2\pi}_0{d\phi}\int^{\frac{\pi}{2}}_0{E{\cos \theta\ }\ R^2{\sin \theta\ }d\theta}\\ &= 2\pi ER^2\int^{\frac{\pi}{2}}_0{\underbrace{{\sin \theta\ }{\cos \theta\ }}_{\frac{1}{2}{\sin 2\theta\ }}d\theta} \end{align*}
\begin{align*} \Rightarrow {\Phi }_E &=2\pi ER^2\left(\frac{1}{2}\right){\left(-\frac{1}{2}{\cos 2\theta\ }\right)}^{\frac{\pi}{2}}_0\\ &=-\frac{1}{2}\pi ER^2\left({\cos 2\frac{\pi}{2}\ }-{\cos 0\ }\right)\\ &=\pi ER^2 \end{align*}
In above, $dA=R^2{\sin \theta\ }d\theta d\phi $ is the area element of the sphere.
Solution 2: all of the electric lines through the circle at the bottom of the hemisphere, passing through the area of the hemisphere. So by calculating the flux through the circle, one can find the flux through the hemisphere but the important thing to remember is that, by convention, the flux through the circle is incoming and is negative of the outgoing flux through the hemisphere that is ${\Phi }_E\left(circle\right)=-{\Phi }_E(hemisphere)$. Therefore, by definition of the electric flux through a surface is
\[{\Phi }_E\left(circle\right)=\vec{E}.\hat{n}\ A=E\left(+\hat{k}\right).\left(-\hat{k}\right)\left(\pi R^2\right)=-\pi ER^2\]
Note: the normal vector $\hat{n}$ is always out of one side of a surface (as in the above case).
A sphere of radius $R$ contains a total charge $Q$ which is uniformly distributed throughout its volume. At a distance $2R$ from the center of the sphere we place a point charge $q$. What is the value of $q$ which makes the electric field at the point $P$ on the surface zero?
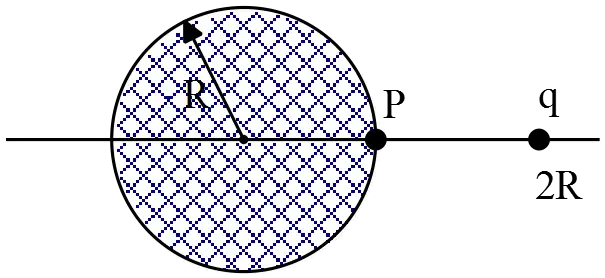
First we must determine the magnitude of the electric field of a uniformly charged 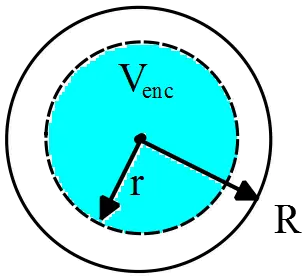 sphere at its surface. To do this, using Gauss's law we obtain the electric field inside of it
sphere at its surface. To do this, using Gauss's law we obtain the electric field inside of it
\[\oint_S{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}\]
Where the symbol $\oint $ represents the integral over a closed surface and $Q_{enc}$ is stands for the charge enclosed by the closed surface $S$. To compute the electric field inside of such a sphere, one must consider an imaginary spherical surface of radius $r$ , called Gaussian surface, then evaluate the integral above as follows
\[\oint_S{{\vec{E}}_{in}.\hat{n}dA}=E_{in}\oint_s{dA}=\frac{Q_{enc}}{\epsilon_0}\]
We have taken $E_{in}$ out of the integral because it is constant everywhere on the surface. The integral of $dA$ over the spherical surface is just the total area of it that is $4\pi r^2$. By definition of the volume charge density, we can find the amount of charge enclosed by this imaginary sphere.
\[Q_{enc}=\rho V_{enc}=\frac{4}{3}\pi r^3 \rho\]
using this, the electric field inside of a uniformly charged sphere with charge density $?$ is
\[E_{in}\left(4\pi r^2\right)=\frac{4}{3}\pi r^3\frac{\rho}{\epsilon_0}\Rightarrow E_{in}=\frac{\rho}{3\epsilon_0}r\]
Since $\rho$ is constant, we can use this fact to express $E_{in}$ in terms of the total charge of sphere $Q$.
\[\rho=\frac{Q}{V_{tot}}=\frac{Q}{\frac{4}{3}\pi R^3}\]
By substituting $\rho$ into $E_{in}\left(r\right)$, we get
\[E_{in}\left(r\right)=\frac{1}{3\epsilon_0}\frac{Q}{\frac{4}{3}\rho R^3}r=\frac{Q}{4\pi \epsilon_0}\frac{r}{R^3}\]
Setting $r=R$, we obtain the electric field of a uniformly charged sphere at its surface
\[{\vec{E}}_{in}\left(r=R\right)=\frac{Q}{4\pi \epsilon_0}\frac{1}{R^2}(\hat{i})\]
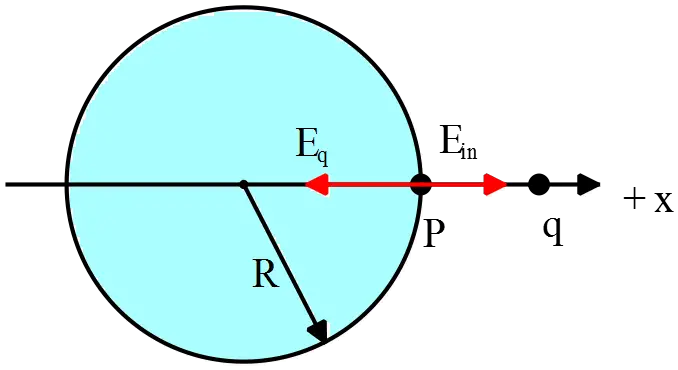
Now compute the electric field due to the positive point charge $q$ at point $P$ as follows
\[{\vec{E}}_q=\frac{1}{4\pi \epsilon_0}\frac{q}{r^2}(-\hat{i})=\frac{1}{4\pi \epsilon_0}\frac{q}{R^2}(-\hat{i})\]
By applying the superposition principle, we can find the net electric field of above configuration at point $P$
\[{\vec{E}}_{net}={\vec{E}}_{in}\left(r=R\right)+{\vec{E}}_q=\frac{Q}{4\pi \epsilon_0}\frac{1}{R^2}(\hat{i})+\frac{1}{4\pi \epsilon_0}\frac{q}{R^2}\left(-\hat{i}\right)\]
Setting $E_{net}=0$, we can determine the unknown charge $q$
\[E_{net}=0\Rightarrow \frac{Q}{4\pi \epsilon_0}\frac{1}{R^2}-\frac{1}{4\pi \epsilon_0}\frac{q}{R^2}=0\ \]
\[\Rightarrow \ q=Q\ \]
In above, we have used the convention that direction of the electric field of a positive point charge is outward and vice versa.
A point charge of charge $-Q$ is placed at the center of a solid spherical conducting shell of inner radius $R$ and outer radius $2R$. The shell is in static equilibrium and has a net charge $+2Q$. What is the total charge on the outer surface (at $r=2R$) of the shell?
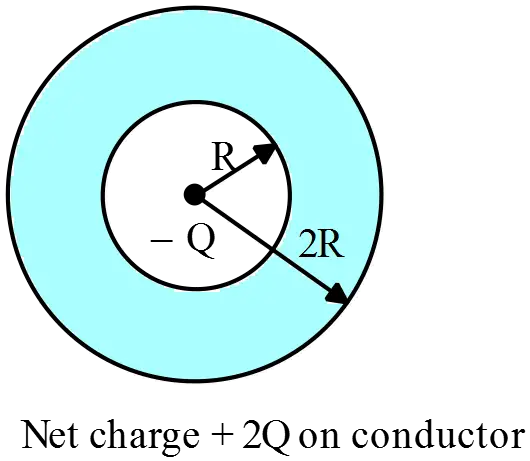
The charge $-Q$ induces charge $+Q$ on the inner sphere and similarly this charge induces charge $-Q$ on the outer sphere of radius $2R$. Since the electric field inside a conductor in electrostatic equilibrium is zero and since it is stated that the shell has a net charge $+2Q$, we conclude that the excess charge must be reside on the outer surface of the shell. So by summing these two contribution over the outer surface, one can find the total free charge uniformly distributed on the outer surface to be
\[Q^{'}=+2Q+\left(-Q\right)=+Q\]
A solid conducting sphere carrying charge $q$ has radius $a$. It is inside a concentric 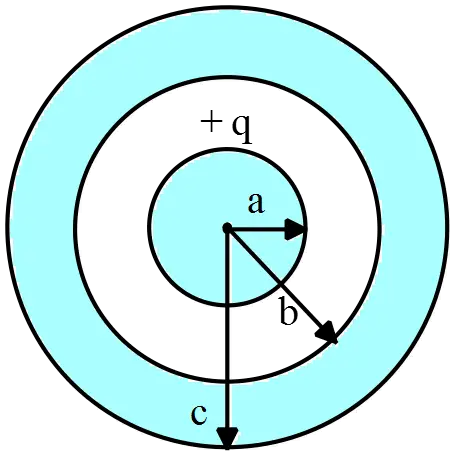 hollow conducting sphere with inner radius $b$ and outer radius $c$. The hollow sphere has no net charge.
hollow conducting sphere with inner radius $b$ and outer radius $c$. The hollow sphere has no net charge.
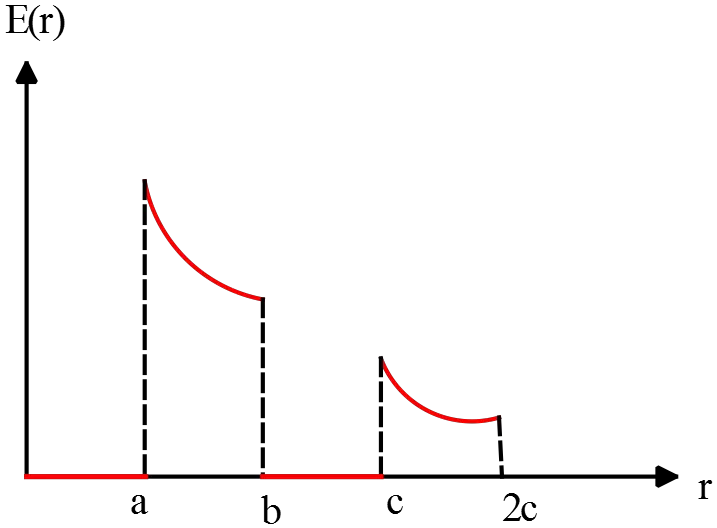
(a) Derive expressions for the electric field magnitude in terms of the distance $r$ from the center for the region $r<a\ ,\ a<r<b\ ,\ b<r<c\ $and $r>c$.
(b) Graph the magnitude of the electric field as a function of $r$ from $r=0$ to $r=2c$.
(c) What is the charge on the inner surface and on the outer surface of the hollow sphere?
(a) In such a problem, one can use the Gauss's law to find the electric field 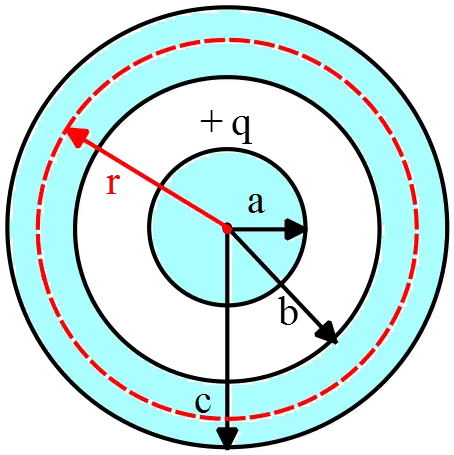 everywhere. Gauss's law states that the electric flux through any closed surface $S$ is equal to the charged enclosed by it divided by $\epsilon_0$. The mathematical form of it is
everywhere. Gauss's law states that the electric flux through any closed surface $S$ is equal to the charged enclosed by it divided by $\epsilon_0$. The mathematical form of it is
\[\oint_s{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}\]
To use the Gauss's law, we must firstly consider a closed surface which is called Gaussian surface. This surface has the same symmetry as the electric field. In this case, the Gaussian surface must be a spherical surface of radius $r$ concentric with the conducting charged sphere of radius $a$.
Note: although the Gauss's law is true for any surface surrounding a charged configuration, but it is useful only when we choose a Gaussian surface to match the original symmetry of the problem.
To find the electric field in region $r<a$, the Gaussian surface is inside the sphere of radius $a$. Since inside this surface does not any enclosed charge, so there is no flux through it, so
\[\oint_s{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}=0\Rightarrow E\left(r<a\right)=0\]
In the region $a<r<b$, the Gaussian surface encloses the charged sphere $q$, so
\[\oint_s{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}=\frac{q}{\epsilon_0}\Rightarrow E\left(a<r<b\right)\oint_s{dA}=\frac{q}{\epsilon_0}\]
\[\Rightarrow \ E\left(a<r<b\right)=\frac{q}{4\pi \epsilon_0r^2}\]
Since $E$ is constant and perpendicular everywhere on the Gaussian surface, so we have taken out of integral. The closed integral $\oint_s{dA}$ is the surface area of the sphere. In the case of sphere, the normal vector $\hat{n}$ is along the radial direction i.e. $\hat{n}=\hat{r}$. Since inside the Gaussian surface there is a positive charge then the electric field point away from the center or is radially outward i.e. $\vec{E}=E\left(r\right)\hat{r}$.
Region $b<r<c$ lies inside the conductor. Using this fact the electric field inside a conductor is zero , so $E\left(b<r<c\right)=0$. In region $r>c$, the net charge encloses by the Gaussian surface is $+q$, so in this region the electric field is
\[\oint_s{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}=\frac{q}{\epsilon_0}\Rightarrow E\left(r>c\right)=\frac{q}{4\pi \epsilon_0r^2}\]
(b) The graph is as follows
(c) The free charge $q$ inside the sphere of radius $a$ induces the charge $-q$ on the inner surface and subsequently this charge also induces the charge $+q$ on the outer surface of the spherical shell.
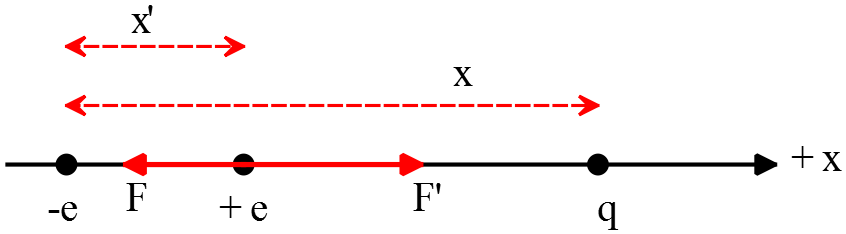
A electron is fixed at the position $x=0$, and a second charge $q$ is fixed at $x=4\times {10}^{-9}\ {\rm m}$ (to the right). A proton is now placed between the two at $x^{'}=1\times {10}^{-9}\ {\rm m}$. What must the charge $q$ be (magnitude and sign) so that the proton is in equilibrium?
The magnitude of the electric force between two point charges $q$ and $q^{'}$ located at distance $r$ from each other is given by the Coulomb's law as follows
\[F=k\frac{\left|qq^{'}\right|}{r^2}\]
Where $k=9\times {10}^9\ {\rm N.}{{\rm m}}^{{\rm 2}}/C^2$. The directions of the forces the two charges exert on each other are always along the line joining them.
The figure below is a free body diagram for proton. Let us consider the charge $q$ to be positive. In such a case, $F$ is the force exerted on the proton by the electron and $F^{'}$ is the force exerted by the charge $q$ on it. Now compute these forces and use the superposition principle to find the total force acting on the proton.
\[{\vec{F}}_{tot}=\vec{F}+{\vec{F}}^{'}=k\frac{\left|\left(-e\right)(+e)\right|}{{{x^{'}}^2}}\left(-\hat{i}\right)+k\frac{\left|\left(+e\right)q\right|}{{\left(x-x^{'}\right)}^2}\left(+\hat{i}\right)\]
Since the charge $q$ is in equilibrium state so the total force exerted on it must be zero
\[{\vec{F}}_{tot}=0\ ,{\rm \ equilibrium\ condition}\]
\[k\frac{\left|\left(-e\right)\left(+e\right)\right|}{{x^{'}}^2}\left(-\hat{i}\right)+k\frac{\left|\left(+e\right)q\right|}{{\left(x-x^{'}\right)}^2}\left(+\hat{i}\right)=0\]
\[\Rightarrow \frac{e}{{x^{'}}^2}=\frac{\left|q\right|}{{\left(x-x^{'}\right)}^2}\Rightarrow e{\left(x-x^{'}\right)}^2=\left|q\right|{x^{'}}^2\]
\[e{\left(4\ {\rm nm-1nm}\right)}^{{\rm 2}}=\left|q\right|{\left(1{\rm nm}\right)}^{{\rm 2}}\]
\[\Rightarrow \ \left|q\right|=9e\]
If we assume that the charge $q$ is negative, we get the same result.
An ink droplet of mass $m$ and charge $q$ is injected horizontally with an initially velocity ${\vec{v}}_0$ into a region with an electric field $\vec{E}$ which is perpendicular to ${\vec{v}}_0$. If a piece of paper is positioned a distance $d$ away from the injection point as shown in the figure, what is the vertical deflection $y$ of the droplet?
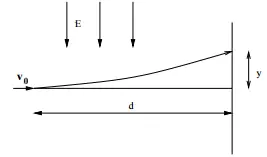
The electric force acting on the charge $q$ is $\vec{F}=q\vec{E}=q\left|\vec{E}\right|(-\hat{j})$, so using Newton's second law the magnitude of acceleration in the $y$ direction is
\[a_y=\frac{F}{m}=\frac{q\left|\vec{E}\right|}{m}\]
The initial velocity and height of the droplet is $v_0=0\ ,\ y_0=0$, respectively. Thus by applying the following kinematical relation $y=\frac{1}{2}at^2+v_0t+y_0$, we can obtain the distance traveled in $y$ direction in terms of the elapsed time $t$.
\[y=\frac{1}{2}\left(\frac{q\left|\vec{E}\right|}{m}\right)t^2\]
The elapsed time in $x$ and $y$ directions is the same. There are no forces in the $x$ direction so that the velocity $v_x=v_0$ is constant. Using the equation of uniform motion $x=vt$, we can find the elapsed time $t$ as follows
\[d=v_0t\Rightarrow t=\frac{d}{v_0}\]
By substituting $t$ into the $y\ $equation above, we get
\[y=\frac{1}{2}\left(\frac{q\left|\vec{E}\right|}{m}\right){\left(\frac{d}{v_0}\right)}^2=\frac{q\left|E\right|d^2}{2mv^2_0}\]
A very long, uniform line of charge with positive linear charge density $+\lambda$ lies  along the $x$ axis. An identical line of charge lies along the $y$ axis.
along the $x$ axis. An identical line of charge lies along the $y$ axis.
(a) Determine the electric field $\vec{E}(x,y)$ for all points in the $x-y$ plane.
(b) Determine the change in the electrostatic potential $\Delta V$ between the points $x=a,y=a$ and $x=a,y=3a$.
(c) Determine $\Delta V$ between the points $x=a,y=a$ and $x=3a,y=a$.
(d) How much work must be done to move a small negative charge $-q$ from the point $x=3a,y=3a$ to the point $x=a,y=a$?
(e) For a very long linear charge distribution, we do not define the zero of electrostatic potential to be an infinity. Why not?
(a) Use Gauss's law to find the electric field due to a long uniform line of charge with charge density $\lambda$. In this case, the Gaussian surface must be cylindrical to match the symmetry of the problem so the Gaussian surface is a coaxial cylinder with the wire with length $L$ and radius $R$. The direction of $\vec{E}$ is also radial. Therefore,
\[\oint_S{\vec{E}.\hat{n}dA}=\frac{Q_{enc}}{\epsilon_0}\to E_R\oint_S{dA}=\frac{1}{\epsilon_0}\int^L_0{\lambda dx}\]
\[\Rightarrow E_R\left(2\pi RL\right)=\frac{1}{\epsilon_0}\lambda L\Rightarrow E_R=+\frac{\lambda}{2\pi\epsilon_0R}\]
In above, $\oint_s{dA}$ is the area of the curved surface of the cylinder. Since the $\vec{E}$ is radially outward from the wire, the contributions due to left $\hat{n}=-\hat{x}$ and right $\hat{n}=+\hat{x}$ end of cylinder are zero i.e. $\vec{E}.\hat{n}=0$. $R$ is the distance from the wire.
Therefore, the line $+\lambda$ ,which is lies along the $x$ axis, at distance $y$ from it produced the electric field
\[{\vec{E}}_1=\frac{+\lambda}{2\pi\epsilon_0y}\ \hat{y}\]
And the line $+\lambda$, which is lies along the $y$ axis, at distance $x$ from it produce the following electric field
\[{\vec{E}}_2=\frac{+\lambda}{2\pi\epsilon_0x}\hat{x}\]
Thus, the total electric field at a point in the $x-y$ plane is
\[{\vec{E}}_{tot}=\frac{+\lambda}{2\pi\epsilon_0}\left(\frac{1}{y}\ \hat{y}+\frac{1}{x}\ \hat{x}\right)\] 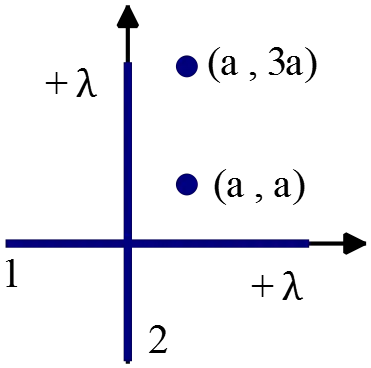
(b) The electric potential between $a$ and $b$ is defined as $V_b-V_a=-\int^b_a{\vec{E}.d\vec{l}}$. we are moving perpendicular to the wire 1 and subsequently parallel to the wire $2$, so wire
$2$ does not contribute to the potential difference. In this case, $d\vec{l}=dy\hat{y}$.
\[\Delta V=-\int^{3a}_a{{\vec{E}}_1.d\vec{l}}=-\int^{3a}_a{\frac{\lambda}{2\pi\epsilon_0y}dy}=-\frac{\lambda}{2\pi\epsilon_0}{\left.{\ln y\ }\right|}^{3a}_a\]
\[\therefore \ \Delta V=-\frac{\lambda}{2\pi\epsilon_0}{\ln 3\ }\]
So going from $y=a$ to $y=3a$ the potential is decreasing since we are moving away 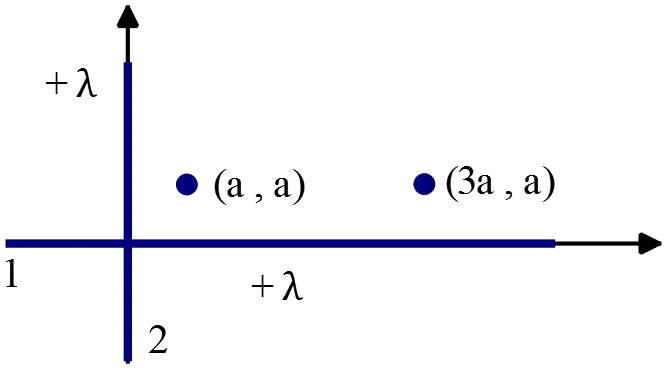 from the charged line $1$.
from the charged line $1$.
(c) In this case, we are approaching perpendicularly to the wire $2$. In this direction we have change in the electric field of ${\vec{E}}_2$, so only this wire contribute to the potential difference.
\[\Delta V=-\int^{3a}_a{E_2\hat{x}.dx\ \hat{x}}=-\int^{3a}_a{\frac{\lambda}{2\pi\epsilon_0x}dx}=-\frac{\lambda}{2\pi\epsilon_0}{\left.{\ln x\ }\right|}^{3a}_a\]
\[\therefore \Delta V=-\frac{\lambda}{2\pi\epsilon_0}{\ln 3\ }\]
(d) The work done on a point charge $q$ to move it from point $a$ to $b$ in an external 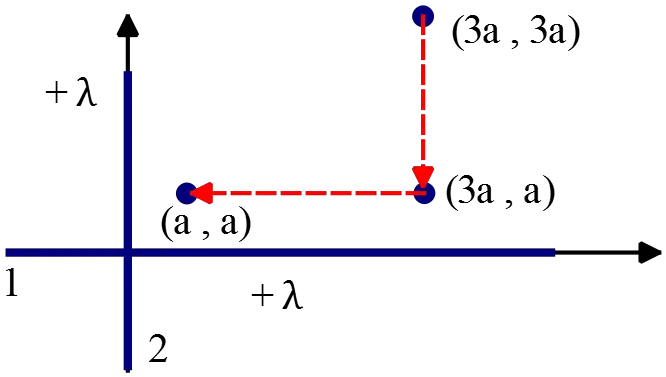 electric field with a potential difference $\Delta V$ is found by $W=q\Delta V$.
electric field with a potential difference $\Delta V$ is found by $W=q\Delta V$.
To going from $(3a,3a)$ to $\left(a,a\right)$ we can consider the following path
\[\left(3a,3a\right)\xrightarrow{1}\left(3a,a\right)\xrightarrow{2}(a,a)\]
In the path 1, we have
\[\Delta V_1=V_{(3a,3a)}-V_{(3a,a)}=-\int^{3a}_a{{\vec{E}}_1\hat{y}.dy\left(-\hat{y}\right)}=\frac{\lambda}{2\pi\epsilon_0}{\ln 3\ }\]
In the path 2, we also have
\[\Delta V_2=V_{3a,a}-V_{a,a}=-\int^{3a}_a{E_2\hat{x}.dx\left(-\hat{x}\right)}=\frac{\lambda}{2\pi\epsilon_0}{\ln 3\ }\ \]
The signs in the above potentials changes because we are moving in the opposite direction as was considered in previous parts. Therefore, the total electric potential between the $(3a,3a)$ and $(a,a)$ is
\[\Delta V=\Delta V_1+\Delta V_2=\frac{\lambda}{\pi\epsilon_0}{\ln 3\ }\]
The work done on the charge $q$ by an external agent is found as
\[W=-q\Delta V=-\frac{q\lambda}{2\pi\epsilon_0}{\ln 3\ }\]
The electric fields due to the line of charges does positive work on the external charge $q$.
(e) Since in this case, unlike the spherical charged distribution, the charge is extended to the infinity and thus at that point we have charge and electric field!
A charge $Q$ is placed on a metal sphere (sphere $1$) of radius $R_1$ . Very far from this sphere is a second sphere (sphere $2$) of radius $R_2$ which is initially uncharged. If the two spheres are connected by a metal wire, what is the final charge $Q_2$ on sphere $2$?
Once the two spheres are connected, they constitute an equipotential system. In this case, some of the charge $Q$ delivers to the sphere $2$, that is the total charge of the system becomes $Q=Q_1+Q_2$ where $Q_1$ is the new charge on the sphere $1$ and $Q_2$ is one the sphere $2$. Recall that the electric potential due to a sphere of radius $R_1$ and charge $Q_1$ is $V_1=kQ_1/R_1$, and for a sphere of radius $R_2$ with charge $Q_2$ is $V_2=kQ_2/R_2$.
Since after the two spheres connect to each other form an equipotential system, we have
\[V_1=V_1\Rightarrow \frac{kQ_1}{R_1}=\frac{kQ_2}{R_2}\Rightarrow Q_1=\frac{R_1}{R_2}Q_2\]
Substituting $Q_1$ into the $Q=Q_1+Q_2$ and solving for $Q_2$, we obtain
\[Q=\frac{R_1}{R_2}Q_2+Q_2=Q_2\left(1+\frac{R_1}{R_2}\right)\]
\[\Rightarrow Q_2=\frac{QR_2}{R_2+R_1}\]
Three electrons are placed at the vertexes of an equilateral triangle with side length of ${\rm 5.1\ nm}$. A proton is placed at the center of the triangle. What is the potential energy of this arrangement of charges?
The potential energy of two point charges separated by distance $r$ is 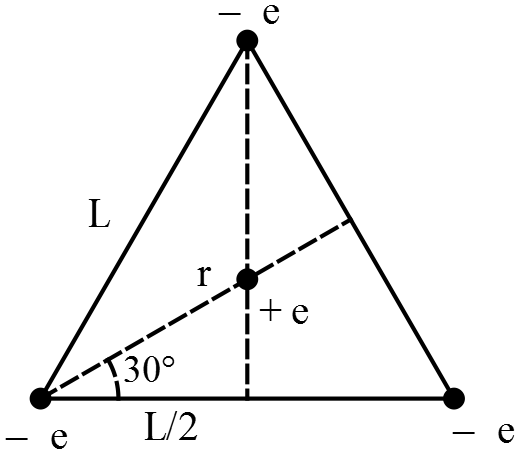
\[U=k\frac{q_1q_2}{r}\]
The potential energy is a scalar quantity so the total potential energy due to a configuration of point charges is the sum of the potential energy of each pairs of them. In this case, since the distance of charges and their magnitudes are the same so
\begin{align*}
U&=U\left(3\ electrons\ pairs\right)+U\left(3\ (e^++e^-)\ pairs\right)\\
&=3k\frac{\left(-e\right)\left(-e\right)}{L}+3k\frac{\left(+e\right)\left(-e\right)}{r}
\end{align*}
$r$ is the distance between electron and proton which can be computed from the geometry below
\begin{align*}
\therefore U_{tot}&=+3k\frac{e^2}{L}-\frac{3ke^2}{\frac{L}{2{\cos 30{}^\circ \ }}}\\
&=\frac{3ke^2}{L}\left(1-2{\cos 30{}^\circ \ }\right)\\
&=\frac{3\left(9\times {10}^9\right){\left(1.6\times {10}^{-19}\right)}^2}{5.1\times {10}^{-9}}\left(1-2\, \cos 30{}^\circ \right)\\
&=-9.92\times {10}^{-20}\ {\rm J}
\end{align*}
From the definition of cosine of an angle in the triangle above, we get
\[{\cos 30{}^\circ \ }=\frac{\frac{L}{2}}{r}\Rightarrow r=\frac{L}{2{\cos 30{}^\circ \ }}\]
An electron was accelerated from rest through a potential difference of ${\rm 9900\ V}$. What is its speed? ($m_e=9.31\times {10}^{-31}{\rm kg}$).
Conservation of mechanical energy is conserved, $\Delta K+\Delta U=0$. Recall that the potential energy of a point charge moving through a potential difference $\Delta V$ is $\Delta U=q\Delta V$. Since the electron accelerated from rest; hence $\Delta K=K_f-K_i=\frac{1}{2}mv^2_f-0$. A negative charge moves against the electric field which is the direction of the decreasing potential energy i.e. $\Delta V=V_f-V_i<0$. Thus
\[\Delta K+\Delta U=0\]
\[\frac{1}{2}m\left(v^2_f-v^2_0\right)+q\Delta V=0\Rightarrow v_f=\sqrt{-\frac{2q\Delta V}{m}}\]
Electron has $q=-e=-1.6\times {10}^{-19}\ {\rm C}$
\[\Rightarrow v_f=\sqrt{\frac{2\left(1.6\times {10}^{-19}\right)\left(9900\right)}{9.31\times {10}^{-31}\ {\rm kg}}}=5.83\times {10}^7\frac{{\rm m}}{{\rm s}}\]
An electric field $\vec{E}=\frac{1}{r^2}\ \hat{r}$ is located in the $xy$ plane. What is the potential difference between $r=6\ {\rm m}$ and $r=8\ {\rm m}$?
The electric field $\vec{E}$ and potential difference $V$ are related by
\[\Delta V=V_f-V_i=-\int^f_i{\vec{E}.d\vec{s}}\]
Where $s$ is the displacement vector from point $i$ to point $f$. Note that only the component of the electric field parallel to the line of integration is relevant. Therefore,
\[\Delta V=V\left(r=8{\rm m}\right){\rm -}V\left(r={\rm 6m}\right){\rm =-}\int^{r=8}_{r=6}{\frac{1}{r^2}\hat{r}.dr\hat{r}}={\rm -}\int^{r=8}_{r=6}{\frac{1}{r^2}dr}\]
\[{\rm =-}{\left(-\frac{1}{r}\right)}^8_6=\left(\frac{1}{8}-\frac{1}{6}\right)=\frac{3-4}{24}=-\frac{1}{24}\ {\rm V}\]
In above, $d\vec{s}=dr\ \hat{r}$ is chosen in the radial direction.
The figure shows a current entering a truncated solid cone made of a conducting metal.  The electron drift speed at the ${\rm 3.0\ mm}$ diameter end of the cone is ${\rm 4.0\times }{{\rm 10}}^{{\rm -}{\rm 4}}{\rm \ m/s}$. What is the electron drift speed at the ${\rm 1.0\ mm}$ diameter end of the wire?
The electron drift speed at the ${\rm 3.0\ mm}$ diameter end of the cone is ${\rm 4.0\times }{{\rm 10}}^{{\rm -}{\rm 4}}{\rm \ m/s}$. What is the electron drift speed at the ${\rm 1.0\ mm}$ diameter end of the wire?
An electron in a conductor will propagate randomly or have thermal motion similar to the motion of the molecules of the gas such as air. With applying an electric field, we can change this randomly motions into a uniform motion in one direction with speed $v_d$ which is called drift speed. The typical value for such a speed is about ${10}^{-4}\ {\rm m/s}$.
The relation between current through a wire with cross sectional area $A$ and drift speed of charge carries, the charges that move in a conductor, of charge density $n$ is
\[I=nqAv_d\]
In this figure, the current through $3\ {\rm mm}$ surface is the same as that of $1\ {\rm mm}$ surface that is $I_3=I_1$, therefore
\begin{align*}
A_3v_{d3}=A_1v_{d1}\Rightarrow v_{d1}=\frac{A_3}{A_1}v_{d3}&={\left(\frac{r_3}{r_1}\right)}^2v_{d3}\\
&={\left(\frac{3}{1}\right)}^2\left(4\times {10}^{-4}\right)\\
&=36\times {10}^{-4}\frac{{\rm m}}{{\rm s}}{\rm \ }
\end{align*}
$A=\pi r^2$is the cross sectional area of the circular disk.
If excess charge is put on a spherical conductor,
(a) it remains where it was placed
(b) it spreads a little from where it was placed but not over the whole sphere
(c) it spreads uniformly over the surface of the sphere if the sphere is small
(d) it spreads uniformly throughout the volume of the conductor
(e) it spreads uniformly over the surface of the sphere
The surface of a conductor is an equipotential surface which means that whose surface must be always in equilibrium. Putting an excess charge would disrupt this equilibrium condition on the surface since causes an electric field forms between the accumulation of charges in that point and other points of the surface. This electric field, by definition, causes a change in the electric potential difference between any points on the surface, instead, if the excess charge spreads uniformly over the surface the equipotential condition of the surface is not violated.
The correct answer is E.
Comparing the field of a single point charge with the field of an electric dipole,
(a) the field of the point charge decreases more rapidly with distance
(b) the field of the point charge decreases less rapidly with distance
(c) the field of the point charge decreases more rapidly with distance but only along the dipole axis
(d) the field of the point charge decreases less rapidly with distance but only perpendicular to the dipole axis
(e) the fields decrease equally rapidly with distance
the electric field of a point charge is found as $E=kQ/r^2$, which obeys the inverse-square law but the electric field of an electric dipole, pairs of point charges with equal magnitude and opposite sign separated by a distance $d$, at far away distances from the dipole can be found as
\[{\vec{E}}_{dipole}=\frac{1}{4\pi {\epsilon }_0}\frac{\vec{p}}{r^3}\]
Where $\vec{p}=q\vec{d}$ is the electric dipole moment and $\vec{d}$ is distance vector from the negative charge to the positive charge.
As you can see the electric field of a dipole decreases more rapidly than that of point charges.
The correct answer is B.
An electron traveling north enters a region where the electric field is uniform and points north. The electron:
(a) speeds up
(b) slows down
(c) veers east
(d) veers west
(e) continues with the same speed in the same direction
recall that positive charge moves in direction of electric field and a negative charge moves in opposite direction of electric field. Since the displacement of electron, to north, and direction of the electric field, to north, are in the same direction, the electron is decreasing down.
The correct answer is B.
A $\mathrm{3.5\ cm}$ radius hemisphere contains a total charge of $6.6\times {10}^{-7}\mathrm{C}$. The flux through the rounded portion of the surface is $9.8\times {10}^4\mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}$. The flux through the flat base is:
(a) $0\ \mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}$
(b) $2.3\ \mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}$
(c) $-2.3\ \mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}$
(d) $-9.8\ \mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}$
(e) $9.8\ \mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}$
The amount of electric flux ${\mathrm{\Phi }}_E$ through any closed surface and the associated enclosed total charge is related together by Gauss's law as
\[{\mathrm{\Phi }}_E=\frac{Q_{encl}}{{\epsilon }_0}\]
Hemisphere has two surfaces, rounded and flat base thus the total electric flux through it is
\[{\mathrm{\Phi }}_{E.r}+{\mathrm{\Phi }}_{E.b}=\frac{Q_{encl}}{{\epsilon }_0}\]
\[9.8\times {10}^4+{\mathrm{\Phi }}_{E.b}=\frac{6.6\times {10}^{-7}}{8.854\times {10}^{-12}}\Rightarrow \ {\mathrm{\Phi }}_{E.b}=-2.34\ \mathrm{N.}{\mathrm{m}}^{\mathrm{2}}\mathrm{/C}\]
The correct answer is C.
Charge $Q$ is distributed uniformly throughout an insulating sphere of radius $R$. The magnitude of the electric field at a point $R/2$ from the center is:
(a) $Q/4\pi {\epsilon }_0R^2$
(b) $Q/\pi {\epsilon }_0R^2$
(c) $3Q/4\pi {\epsilon }_0R^2$
(d) $Q/8\pi {\epsilon }_0R^2$
(e) None of these
If we have symmetric configuration, as this case, use Gauss's law to find the electric field at each point of space. To do this, one must suppose a Gaussian surface at the desired point. In this problem, draw a Gaussian surface as sphere of radius of $R/2$ and proceed as follows
\[\oint{\vec{E}.d\vec{A}}=\frac{Q_{encl}}{{\epsilon }_0}\]
Where $Q_{encl}$ is the charge enclosed in the Gaussian surface which here is sphere of radius $R/2$ and is determined by the definition of volume charge density
\[\rho =\frac{Q}{V}\to Q_{encl}=\rho V_{Gauss}=\rho \left(\frac{4}{3}\pi {\left(\frac{R}{2}\right)}^3\right)=\frac{1}{6}\rho \pi R^3\]
Substituting above into Gauss's law, we get
\[E\oint{dA}=\frac{1}{6}\rho \pi R^3\]
The electric field is taken out of the integral since it is constant at the location of the Gaussian sphere by symmetry considerations. The closed integral gives the area of the Gaussian surface. Therefore
\[E\left(4\pi {\left(\frac{R}{2}\right)}^2\right)=\frac{\frac{1}{6}\rho \pi R^3}{{\epsilon }_0}\to \ \ E=\frac{1}{4\pi {\epsilon }_0}\frac{2}{3}\rho \pi R\]
Since the density of the sphere is uniform everywhere so substitute it by the total charge induced on the original sphere of radius $R$ as
\[\rho =\frac{Q}{V}=\frac{Q}{\frac{4}{3}\pi R^3}\]
Therefore
\[E=\frac{1}{4\pi {\epsilon }_0}\frac{2}{3}\frac{Q}{\frac{4}{3}\pi R^3}\pi R=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{{2R}^2}=\frac{Q}{8\pi {\epsilon }_0R^2}\]
The correct answer is D.
If $\mathrm{500\ J}$ of work are required to carry a $\mathrm{40\ C}$ charge from one point to another, the potential difference between these two points is:
(a) $12.5\, \mathrm V$
(b) $20000\, \mathrm V$
(c) $0.08\, \mathrm V$
(d) Depends on the path
(e) None of these
The potential difference between two points is defined as the ratio of the change in electric potential energy to the electric charge which is moved between those points and is written as \[\Delta V=\frac{\Delta U}{q}\]
We know that the work done on a system is stored in its potential energy so, regardless of its sign, we have $W=\Delta U=500\quad \rm J$. Hence, \[\Delta V=\frac{500}{40}=12.5\quad \rm V\] To practice more solved problems on the electric potential, refer here.
The correct answer is A.
The diagram shows four pairs of large parallel conducting plates. The value of the electric potential is given for each plate. Rank the pairs according to the magnitude of the electric field between the plates, least to greatest
(a) 1,2,3,4
(b) 4,3,2,1
(c) 2,3,1,4
(d) 2,4,1,3
(e) 3,2,4,1
The electric field between two large parallel conducting plates is uniform. Recall that the electric field of a positive plane is away from it and a negative plane is toward it, using this hint and the superposition principle determine the electric field between the plate as follows
In above we have used the definition of the uniform electric field in terms of electric potential as $E=V/d$, since the distance between the plates is the same so the correct answer is D.
A particle with a charge of $5.5\times {10}^{-6}\mathrm{C}$is $\mathrm{3.5\ cm}$ from a particle with a charge of $-\mathrm{2.3\times }{\mathrm{10}}^{\mathrm{-}\mathrm{8}}\mathrm{C}$. The potential energy of this two-particle system, relative to the potential energy at infinite separation, is:
(a) $3.3\times {10}^{-2}\mathrm{J}$
(b) $-3.3\times {10}^{-2}\mathrm{J}$
(c) $9.3\times {10}^{-1}\mathrm{J}$
(d) $-9.3\times {10}^{-1}\mathrm{J}$
(e) $0\ \mathrm{J}$
The electric potential energy of a pair of point charges can be found as follows
\[\mathrm U=\frac{1}{4\pi {\epsilon }_0}\frac{q_1q_2}{r}\]
Therefore,
\[U=\left(9\times {10}^9\right)\frac{\left(5.5\times {10}^{-6}\right)\left(-2.3\times {10}^{-8}\right)}{\left(3.5\times {10}^{-2}\mathrm{m}\right)}=-3.3\times {10}^{-2}\mathrm{J}\]
When the point charges are placed at infinity their potential energy is zero!
The correct answer is B.
A hollow metal sphere is charged to a potential $V$. The potential at its center is:
(a) $V$
(b) 0
(c) $-V$
(d) $2\ \mathrm{V}$
(e) $\pi \ \mathrm{V}$
The electric potential between the two point a and b is defined as
\[V_b-V_a=-\int^b_a{\vec{E}.d\vec{s}}\]
Where $\vec{s}$ is the displacement vector from a toward b and is parallel to the field line. The negative sign indicates that the electric potential at point b is lower than at point b.
To find the electric potential it is customary to choose the reference of the electric potential to be $V=0$ at $r_a=\infty $. Therefore find the electric potential between $r_a=\infty $ to $r_b=0$. The electric field inside and outside a conducting shell is $E_{in}=0$ and $E_{out}=kQ/r^2$, where $Q\ $is the total charge on the sphere.
\[V_0-V_{\infty }=-\int^0_{\infty }{\vec{E}.d\vec{s}}=-\int^R_{\infty }{E_{out}dr}-E_{in}\int^0_R{dr}\]
\[V_0-0=-\int^R_{\infty }{\frac{kQ}{r^2}dr}-0\int^0_R{dr}={{\left.\frac{kQ}{r}\right|}^R}_{\infty }=\frac{kQ}{R}\]
\[\Rightarrow V_0=\frac{kQ}{R}=V\]
$kQ/R$ is the electric potential of a conducting charged sphere at its surface.
The correct answer is a.
In the first equality, $\vec{E}.d\vec{s}$ substituted by $Edr$ since the electric field outside is radial and the displacement vector $d\vec{s}$ has been also chosen radially.
Most useful formula in Electrostatic:
Coulomb's law: the force between two charged particle $q_1$ and $q_2$ separated by distance $r$ is
\[F=k\frac{|q_1q_2|}{r^2}\]
where
\[k=\frac{1}{4\pi \epsilon_0}=8.988 \times {10}^{9} \ {\rm N.m^{2}/C^{2}}\]
Electric field:
\[\vec E=\frac{\vec F}{q_0}\]
Electric field of a point charge at distance $r$:
\[\vec E=\frac{1}{4 \pi \epsilon_0}\frac{q}{r^2} \hat{r}\]
Gauss's law:
\[\Phi_B=\int{\vec E \cdot nd\vec A}=\frac{Q_{enclosed}}{\epsilon_0}\]
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
