Inductance Problems and Solutions for AP Physics
In this solved-problem tutorial, some of the most important examples and problems on self-inductance are solved which are at the AP physics C level.
All these problems are closely related to RL series circuit problems.
Solved Problem on Self-Inductance :
Problem (1): Find the self-inductance of a 100-turns solenoid with cross-sectional area $10\,{\rm cm^2}$ and length of $62.8\,{\rm cm}$.
Solution: The self-inductance of a solenoid depends only on its geometric factors which are its length $\ell$, number of turns $N$, and cross-sectional area $A$. All these factors are related together by the following formula \[L=\frac{\mu_0 N^{2} A}{\ell}\]Therefore, by putting values into above, we have \[L=\frac{(4\pi\times 10^{-7})(100)^{2}(10\times 10^{-4})}{62.8\times 10^{-2}}=2\times 10^{-5}\,{\rm H}\]The SI unit of area is $m^2$, so we converted the the given $cm^2$ to SI units as below \[\rm{1\, cm^{2}=(10^{-2}\,m)^{2}=10^{-4}\,m^2}\]
Are you getting ready for the AP Physics 2 exam? Read this:
AP Physics 2: Circuits Practice Problems with Answers
Problem (2): There is a solenoid with an inductance $0.285\,{\rm mH}$, a length of $36\,{\rm cm}$, and a cross-sectional area $6\times 10^{-4}\,{\rm m^2}$.
(a) Find the number of turns of the solenoid.
(b) Suppose at a specific time the emf is $-12.5\,{\rm mV}$ find the rate of change of the current at that time.
Solution: The self-inductance of a solenoid with length $\ell$, $N$ turns, and cross-sectional area $A$ is given by formula \[L=\frac{\mu_0 N^{2} A}{\ell}\]
(a) In this problem, the number of turns is unknown, so rearranging the above expression and solving for $N$, we get \[N^{2}=\frac{L\ell}{\mu_0 A}=\frac{(0.285\times 10^{-3})(0.36)}{(4\pi\times 10^{-7})(6\times 10^{-4})}\]Taking the square root of both sides, gets the number of turns of the solenoid $N=369$.
(b) A changing current causes a self-induced emf in the solenoid whose magnitude is determined by formula \[\mathcal{E}_L=-L\frac{di}{dt}\] Where the negative indicates the direction of the emf. Putting known values into above and solving for $di/dt$, we get \begin{align*} \mathcal{E}_L &=-L\frac{di}{dt}\\ \\ -12.5&=-0.285\,\frac{di}{dt} \\ \\ \Rightarrow \frac{di}{dt} &= +43.8\quad {\rm A/s}\end{align*} The positive shows that the current is increasing. On the other hand, we can deduce that the induced emf is in the opposite direction of the current in the circuit.
Problem (3): A $500$-turn solenoid have a cross-sectional area $20\,{\rm m^2}$. If its self-inductance is $20\,{\rm H}$, then find the length of the solenoid.
Solution: The self-inductance of a solenoid with $N$ turns, length of $\ell$, and cross-sectional area $A$ is given by the following formula \[L=\frac{\mu_0 N^{2} A}{\ell}\] Putting the values into the above formula and solving for the unknown length $\ell$, we get \[\ell=\frac{(4\pi\times 10^{-7})(500)^{2}(20)}{20}=0.314\,{\rm m}\] Thus, the solenoid has a length of $31.4\,{\rm cm}$.
Problem (4): A solenoid with $100$ turns have a length of $25\,{\rm cm}$ and loop's radius of $10\,{\rm cm}$. The current in it is changing constantly from $30\,{\rm A}$ to zero in $0.02\,{\rm s}$. What is the self-induced emf of the solenoid?
Solution: A changing current is related to a changing magnetic flux using the definition of self-inductance as $\Delta \Phi=L\Delta i$, where $\Phi$ is the total magnetic flux through a coil of wire having $N$ turns which is related to the flux through each turn as $\Phi=N\phi$. Thus, the self-inductance is \[L=\frac{\Phi}{i}=\frac{N\phi}{i}\] Recall that the magnetic flux formula through each turn of a solenoid is $\phi=(\mu_0 \frac N\ell i)A$ where $\ell$ and $A$ are the length and cross-sectional area of the solenoid, respectively.
Consequently, the inductance of a solenoid with $N$ turns is given by the below formula \[L=\frac{N\phi}{i}=\frac{\mu_0 N^{2}A}{\ell}\]As you can see, the solenoid inductance depends on the geometric factors $\ell$ and $A$ and on$\mu_0$ and does not depend on the variation of the current.
Thus, substituting the known values into the above formula, we get \[L=\frac{(4\pi \times 10^{-7})(100)^{2}(\pi (0.1)^{2})}{0.25}=1.5\,{\rm mH}\]
Problem (5): At the moment that the rate of change of the current through an ideal inductor is increasing as $0.064\,{\rm A/s}$, the magnitude of the self-induced emf is $0.016\,{\rm V}$.
(a) What is the inductance of the inductor?
(b) Let this inductor be a $400$-turns solenoid. How much magnetic flux passes through each turn of it when the current is $0.720\,{\rm A}$?
Solution: A time-varying current through a solenoid creates an emf which is related to each other by the following formula \[\mathcal{E}_L=-L\frac{di}{dt}\] Where the minus sign indicates the direction of the self-induced emf by Lenz's law. To find its magnitude, we should drop its negative.
(a) Applying the above equation and solving for unknown inductance $L$, we get \begin{align*} \mathcal{E}_L&=L\frac{di}{dt}\\ \\ 0.016&=L\,(0.064) \\ \\ \Rightarrow L&=0.25\quad {\rm H}\end{align*}
(b) Recall that when the current through an inductor is increasing, its magnitude varies as below \[I=I_0\left(1-e^{-Rt/L}\right)\] so at time $t=0$ the current is zero.
On the other hand, the definition of inductance as $N\Delta \phi=L\Delta i$ relates the difference in magnetic flux through each turn $\phi$ to the difference in the currents. We can use this definition to find the flux through each turn of a $N$-turn solenoid. \begin{align*} N\Delta \phi&=L\Delta i \\ N(\phi_2-\phi_1)&=L(i_2-i_1)\\ (400)(\phi_2-0)&=(0.25)(0.72-0)\\ \Rightarrow \phi_2&=0.45\,{\rm mWb}\end{align*}In the above, $\phi_1$ and $i_1$ are flux and current at time $t=0$ when there is no current in the circuit as well as the magnetic flux.
Problem (6): In a $500$-turn coil, the current is changing from $2\,{\rm A}$ to $2.05\,{\rm A}$ in the time interval $\Delta t$. During this time, the flux changes from $5000\,{\rm \mu Wb}$ to $5025\,{\rm \mu Wb}$. What is the self-inductance of the coil in henry?
Solution: Recall that where there is a changing magnetic flux, an electromotive force, emf $\mathcal{E}$, is produced in the circuit as \[\mathcal{E}=-\frac{d\Phi}{dt}\]
On the other hand, the rate of change of the flux is related to the rate of change of the current using the definition of self-inductance $\Phi=LI$. Thus, this time the induced emf is written as \[\mathcal{E}=-\frac{d\Phi}{di}=-L\frac{di}{dt}\]
If time interval isn't infinitesimal we have \[\mathcal{E}=-\frac{\Delta \Phi}{\Delta i}=-L\, \frac{\Delta i}{\Delta t}\] Putting the known values into above formula, we get \begin{align*} -\frac{\Delta \Phi}{\Delta i}&=-L\frac{\Delta i}{\Delta t}\\ \\ \frac{5025-5000}{\Delta t}&=L \frac{2.05-2}{\Delta t}\\ \\ 25&=L\times 0.05 \\ \\ \Rightarrow L&= 500 \quad {\rm H}\end{align*}
Problem (7): At a given instant of time, the current and induced emf in an inductor are shown below.
(a) Is the current increasing or decreasing?
(b) If the induced emf is $25\,{\rm V}$ and the rate of change of the current is $10\,{\rm kA/s}$, then find the inductance of the inductor.
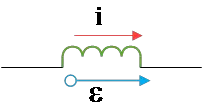
Solution: According to the section of Faraday's law of induction problems, self-induced emf is given by formula \[\mathcal{E}_L=-L\frac{di}{dt}\] Where $L$ is the self-inductance of the inductor and the negative also indicates the direction of the emf.
As you can see, if the rate of change of the current is increasing, $di/dt>0$, then self-induced emf is negative and directed in the opposite direction of the current and vice versa.
(a) In this problem, the current and emf are in the same direction, so the rate of change of current must be negative to cancel out the minus sign in the formula and create a positive emf.
Consequently, the current through this inductor is decreasing i.e. $di/dt<0$.
(b) Substituting the known values $di/dt=-30\,{\rm kA/s}$ and $\mathcal{E}_L=25\,{\rm V}$ into the self-induced emf formula and solving for the inductance $L$, we get \begin{align*} \mathcal{E}_L&=-L\frac{di}{dt}\\ \\25&=-L\left(-10\times 10^{3}\right)\\ \\ \Rightarrow L&=2.5\quad {\rm mH}\end{align*}
Problem (8): In the figure below, the current-vs-time graph for a $4\,{\rm H}$ inductor is depicted. What is the magnitude of the induced emf in the following time intervals?
(a) $0\leq t \leq 2$
(b) $2\leq t \leq 5$
(c) $5\leq t \leq 6$
Solution: When the current in an inductor is changing, the magnetic flux is also changing. Consequently, according to Faraday's law, the induced emf is obtained as $\mathcal{E}=-L\frac{\Delta i}{\Delta t}$, where the negative is due to Lenz's law.
(a) In this time interval, the current increases from zero to $7\,{\rm A}$ so $\Delta i=7\,{\rm A}$ and \[\Delta t=2\times 10^{-3}\,{\rm s}\]Thus, the induced emf is \[\mathcal{E}=-4\times \frac{7}{2\times 10^{-3}}=-14\,{\rm kV}\]
(b) Here, the current is decreasing and its rate of change is \[\frac{\Delta i}{\Delta t}=\frac{5-7}{3\times 10^{-3}}=-666.6\,{\rm A/s}\]. Thus, the self-induced emf is \[\mathcal{E}=(-4)\times (-666.6)=2666.6\,{\rm V}\]
(c) In this time interval the current is also decreasing at a rate of \[\frac{\Delta i}{\Delta t}=\frac{0-5}{1\times 10^{-3}}=-5000\,{\rm A/s}\]Therefore, the induced emf is \[\mathcal{E}=(-4)\times (-5000)=20\,{\rm kV}\]
As you can see the current and induced emf are in opposite directions only in the time interval $[0,2]$ and are in the same direction at other times which is expected from Lenz's law.
Problem (9): The current in a long solenoid with an inductance $L=0.5\,{\rm H}$ is varying as $I(t)=0.2\sin (500t)$. Find the maximum value of the induced emf in the solenoid.
Solution: The varying current produces an emf in an inductor (solenoid or coil of wire) with self-inductance $L$ as below \[\mathcal{E}_L=-L\frac{di}{dt}\] Thus, the self-induced emf in the solenoid is \begin{align*}\mathcal{E}_L&=-(0.5)\,\frac{d}{dt}\left(0.2\sin (500t)\right) \\ \\ &=-(0.5)(0.2)(500)\cos (500t)\\ \\ &=-50\cos (500t)\end{align*} Recall from trigonometry that the maximum value of cosine function is $1$ so the maximum value of the induced emf is $\mathcal{E}_L=-50\,{\rm V}$.
The negative shows the direction of the induced emf.
Problem (10): In the figure below, a $0.260\,{\rm H}$ ideal inductor (with zero resistance) is shown. A decreasing current passes through it at a uniform rate $di/dt=-0.0180$ in the direction shown.
(a) Find the self-induced emf of the inductor.
(b) Of points a and b, which is at higher potential?
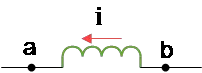
Solution: According to Faraday's law, the self-induced emf of an inductor with inductance $L$ is determined as \[\mathcal{E}_L=-L\frac{di}{dt}\] Where the minus sign indicates the direction of the emf.
(a) Substituting the known values into the above formula, we get \[\mathcal{E}_L=-(0.260)(-0.0180)=+4.68\,{\rm mV}\]
(b) In the formula above, the direction of the induced emf depends on whether the current through an inductor is increasing or decreasing.
A decreasing current, $di/dt<0$, induces an emf in the same direction of the current to prevent further reduction of the current according to Lenz's law.
In this case, the inductor acts like a battery with the following polarities.
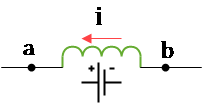
Consequently, as you can see from the above figure, the point $a$ is at a higher potential.
Author: Dr. Ali Nemati
Date Published: 3/24/2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
