- Home
- Physics Problems
- Problems
Solved Problems
A pipe closed at both ends can support standing waves, but the sound cannot get out unless singing in the shower can be compared with singing in a closed pipe.
(a) Show that the wavelength of standing waves in a closed pipe of length $L$ are $\lambda_n=2L/n$ and the frequencies are given by $f_n=\frac{nv}{2L}=nf_0$ where $n=1,2,3,\dots $
(b) Modeling the shower as a closed pipe, find the frequency of the fundamental and the first two overtones if the shower is 2.5 m tall. Are these frequencies audible?
(c) You remembered the outside showers facilities at summer-camp and how your voice sounded different, and you thought-maybe outside camp showers were stopped pipes instead of closed pipes-no ceiling! Repeat your calculations of part (a), and (b) and note the difference in the two situations
(a) Since both ends of the string are fixed, the nodes are formed at these 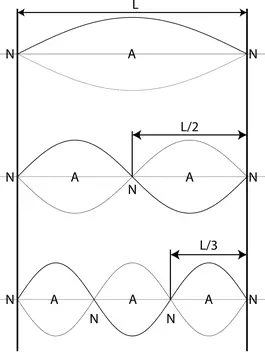 points. Between any two consecutive nodes, there is half a wavelength. Therefore, in general, between any two nodes, we obtain $n$ half a wavelength that is $L=n\ \lambda/2$
points. Between any two consecutive nodes, there is half a wavelength. Therefore, in general, between any two nodes, we obtain $n$ half a wavelength that is $L=n\ \lambda/2$
Where $n=1,2,3,\dots $ represents the nth harmonic mode or the number of nodes. So the wavelength of nth mode and its frequency are given by the following relations
\[\ \lambda_n=\frac{2L}{n}\ ,\ \ f_n=\frac{v}{\lambda_n}=n\frac{v}{2L}\]
(b) $$f_n=\frac{nv}{2L}=\frac{n\left(344\right)}{2\left(2.5\right)}=n\left(68.8\right)=\left(68.8,\ 137.6,206.4\right)\ {\rm Hz}$$
(c) In this case, one end of the pipe is open and the other is close (fixed) so at the open-end forms an anti-node and the fixed end forms a node. Between 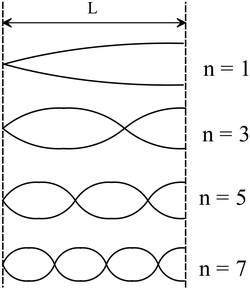 any consecutive node and anti-node, there is one fourth of a wavelength that is in general
any consecutive node and anti-node, there is one fourth of a wavelength that is in general
\[L=n\frac{\lambda}{4}\Rightarrow \lambda_n=\frac{4L}{n}\ \ and\ f_n=\frac{v}{\lambda_n}=n\frac{v}{4L}\]
But here, $n=1,3,5,\dots $ (the number of nodes). The three consecutive modes are
\[f_n=n\left(\frac{344}{4\times 2.5}\right)=n\left(34.4\right)\Longrightarrow \left(34.4\ ,\ 103.2\ ,\ 172\right)\ {\rm Hz}\]
Note: the audible frequencies are between $20\, {\rm Hz}$ and $20000\, {\rm Hz}$. Therefore, in both cases, the frequencies are audible.
Suppose we have massive rope attached to the ceiling. The bottom end of the rope dangles in midair. The mass of the rope is $2.7\ {\rm kg}$ and its length is $4.5\ {\rm m}$. The bottom end of the rope is shaken and then released to produce a pulse that travels up the rope. What is the speed of the pulse when it is halfway up the rope?
The speed of waves on a string with tension $T$ and linear mass density $\mu$ is given by
\[v=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{T}{\frac{m}{l}}}\]
We can suppose that all of mass of the rope is concentrated in the middle of it, so its tension is $T=\frac{mg}{2}$
\[v=\sqrt{\frac{\frac{mg}{2}}{\frac{m}{L}}}=\sqrt{\frac{gl}{2}}=4.7\ {\rm m/s}\]
(a) The figure shows a snapshot graph at $t=0$ of a sinusoidal wave traveling to the right along a string at $50\ {\rm m/s}$. Write the equation that describes the displacement $D(x,t)$ of this wave. Your equation should have numerical values, including units, for all quantities except $x$ and $t$.
(b) What is the maximum acceleration of any portion of the string described above?
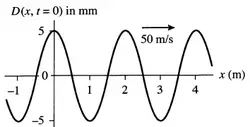
(a) The general form of a wave equation is $D\left(x,t\right)=A{\cos (kx-\omega t+\phi)\ }$ Where $A$ is the amplitude of the wave. Using initial conditions, we find the constants of the above equation.
\[D\left(0,0\right)=5\to 5\,{\cos \phi\ }=5\to \ \phi=0\]
\[k=\frac{2\pi}{\lambda}=\frac{2\pi}{2}=\pi \]
\[\omega=\frac{2\pi}{T}=\frac{2\pi}{\frac{v}{\lambda}}=50\pi \]
\[\therefore D\left(x,t\right)=0.005 \cos (\pi x-50\pi t)\ \]
(b) The acceleration of a travelling wave is defined by the following relation
\[a=\frac{d^2}{dt^2}D\left(x,t\right)=-0.005\ {\left(50\pi\right)}^2{\cos \left(\pi x-50\pi t\right)\ }\]
The above equation is maximum when cosine term be one. Then $a_{max}=120\ {\rm m/}{{\rm s}}^{{\rm 2}}$.
A standing wave is oscillating at $690\ {\rm Hz}$ on a string of mass $1{\rm g}$, as shown in the figure. What is the tension in the string?
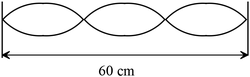
Note: wavelength defined as the distance between two successive picks or valleys. In this figure, there are three valleys or anti-nodes. Each valley is equal to half a wavelength so \[L=3\frac{\lambda}{2}\Rightarrow \ \lambda=\frac{2}{3}L\] Use the relation between wavelength and frequency to find the speed of the wave on the string \[v=\lambda f=\frac{2}{3}Lf=\frac{2}{3}\left(0.6\right)\left(690\right)=276\frac{{\rm m}}{{\rm s}}\] Another relation for speed of the waves on the string is $=\sqrt{\frac{T_S}{\mu}}$ , where $T_s$ is the tension on the string and $\mu=M/L$ is the linear mass density of it. So
\begin{align*}v=\sqrt{\frac{T_S}{\mu}}\Rightarrow T_S&=\mu v^2\\ &=\frac{M}{L}v^2\\ &=\frac{0.001}{0.6}{\left(276\right)}^2\\ &=126.96\ {\rm N}\end{align*}
Two identical loudspeakers are located at points A and B, 2 meters apart. The 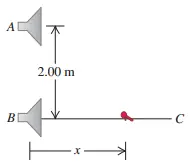 speakers are driven by the same sound source with a frequency of $784\ {\rm Hz}$. Take the speed of sound to be $344\ {\rm m/s}$. A small microphone is moved out from the point $B$ toward the point $C$ a shown.
speakers are driven by the same sound source with a frequency of $784\ {\rm Hz}$. Take the speed of sound to be $344\ {\rm m/s}$. A small microphone is moved out from the point $B$ toward the point $C$ a shown.
(a) At what distance from $B$ will there be destructive interference?
(b) At what distance from $B$ will there be instructive interference?
(c) If the frequency is made low enough, there will be no position along the line $BC$ at which destructive interference can occur. How low must the frequency be for this to be the case?
(a) First, find the difference path of two speakers then use the relation $\Delta D=n\lambda\ ,\ n=1,2,\dots $ for instructive and $\Delta D=n\frac{\lambda}{2}\ ,\ n=1,3,\dots $ for destructive interference.
Let $x$ be the position of microphone along the $BC$ path.
\[\Delta D=\sqrt{x^2+2^2}-x=n\frac{\lambda}{2}\]
\begin{align*}x^2+4&={\left(n\frac{\lambda}{2}+x\right)}^2\\ &={\left(\frac{n\lambda}{2}\right)}^2+x^2+n\lambda x \end{align*}
\begin{gather*} \to n\lambda x=4-{\left(n\frac{\lambda}{2}\right)}^2\\ \Longrightarrow x\left(n\right)=\frac{4}{n\lambda}-n\frac{\lambda}{4}\ ,\ n=1,3,5,\dots \end{gather*}
\[\lambda=\frac{v}{f}=\frac{344}{784}=0.439\ {\rm m}\]
Let $n=1\Rightarrow x=\frac{4}{\left(1\right)\left(0.439\right)}-\frac{1\left(0.439\right)}{4}=9\ {\rm m}$
$n=3\to x=2.7\ {\rm m}$ and so on.
(b) Same procedure as part (a) : $\Delta D=n\lambda\ ,\ n=1,2,\dots \ \ \ \Rightarrow \ x\left(n\right)=\frac{4}{n\lambda}-n\frac{\lambda}{4}\ $
(c) Because in this case there is no position along $BC$ so
\[x=0=\frac{4}{n\lambda}-n\frac{\lambda}{4}\to \ \lambda^2=\frac{16}{n^2}\]
\[n=1\ \Longrightarrow \ \lambda^2_{max}=16\to \lambda_{max}=4\ {\rm m}\]
\[f=\frac{v}{\lambda}=\frac{344}{4}=86\ {\rm Hz}\]
Monochromatic ($\lambda=633\,{\rm nm}$), coherent plane waves of light from a laser are incident on two slits that are separated by a distance $d=0.070\,{\rm nm}$. Independently (without interference effects), each slit illuminates the screen $3.00\ {\rm m}$ away with an intensity of $200\ {\rm W/}{{\rm m}}^{{\rm 2}}$ at the screen.
(a) Determine the positions $y_{min}(m)$ (for $y_{min}>0$) on the screen of the first three intensity minima, where m is the order of each minimum? What is the intensity $I_{min}$ at these positions?
(b) Determine the positions $y_{max}$ (for $y_{max}>0$)on the screen of the first three intensity maxima, where m is the order of each maximum? What is the intensity $I_{max}$ at these positions?
(c) Determine the position $y_{1/4\ }$at which the intensity of the central peak (at $y=0$) drops to $I_{max}/4$. Hint: calculate the angles in radians.
(a) You are asked about $y_{min}$, so we need destructive interference, recall that for occurring such interference, the path lengths taken by the two light rays has to differ by a half-integer number of wavelengths.
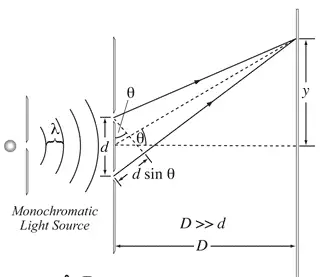
\[\Delta L=d\,{\sin \theta_{min}\ }=\left(m+\frac{1}{2}\right)\lambda\ ,\ m=0,1,2,\dots \ \ \ and\ \ y=D\,{\tan \theta\ }\]
Where $y$ , $d$ and $\theta$ are shown in the figure.
Solving for ${\sin \theta_{min}\ }$, we obtain
\[{\sin \theta_{min}\ }=\left(m+\frac{1}{2}\right)\frac{633\times {10}^{-9}}{0.07\times {10}^{-9}} \]
\[\to \left\{ \begin{array}{lcr} \theta_{min}\left(m=0\right)=0.259{}^\circ \ \ &,& \ \ y_{min}=13.6\, {\rm mm} \\ \theta_{min}\left(m=1\right)=0.777{}^\circ \ \ &,& \ \ y_{min}=40.7\, {\rm mm} \\ \theta_{min}\left(m=2\right)=1.30{}^\circ \ \ &,& \ \ y_{min}=68.1\, {\rm mm} \end{array}\right.\] Due to the completely destructive pattern, intensity at these positions is zero that is $I_{min\ }=0$
(b) Similar above: maxima points are constructive interference $\Delta L=d\,{\sin \theta_{max}\ }=m\lambda\ ,\ m=0,1,2,\dots $
\[{\sin \theta_{max}\ }=\frac{m\lambda}{d}\to \left\{ \begin{array}{lcr} \theta_{max}\left(m=0\right)=0{}^\circ \ \ &,&\ \ y_{max}=0 \\ \theta_{max}\left(m=1\right)=0.518{}^\circ \ \ &,&\ \ y_{max}=27.1\, {\rm mm} \\ \theta_{max}\left(m=2\right)=1.04{}^\circ \ \ &,&\ \ y_{max}=54.5\, {\rm mm} \end{array} \right.\]
Note: the intensity $I$ of a sinusoidal wave with amplitude $E_0$ is given by $I=\frac{1}{2}c\,\epsilon_0E^2_0$
In the interference pattern (two slit) at each point on the screen, there are two waves. In the case of instructive pattern, these waves are in phase and so
\begin{align*}I_{max}&=\frac{1}{2}c\,\epsilon_0{\left(E_0+E_0\right)}^2\\ &=4\frac{1}{2}\epsilon_0\,cE^2_0\\ &=4I_0=4\left(200\frac{{\rm W}}{{{\rm cm}}^{{\rm 2}}}\right)\\&=800\ {\rm W/}{{\rm cm}}^{{\rm 2}}\end{align*}
In general, the intensity pattern for double slit experiment is $I=4I_0\,{{\cos }^2 \left(\frac{\pi d}{\lambda}\,{\sin \theta\ }\right)\ }$ so
\begin{gather*}I_{\frac{1}{4}}=\frac{1}{4}I_{max}\\ \Rightarrow 4I_0\,{{\cos }^2 \left(\frac{\pi d}{\lambda}{\sin \theta_{\frac{1}{4}}\ }\right)\ }=\frac{1}{4}\left(4I_0\right)\\ \to 4\,{{\cos }^2 \left(\frac{\pi d}{\lambda}\,{\sin \theta_{\frac{1}{4}}\ }\right)\ }=1\end{gather*}
\[\Rightarrow \theta_{\frac{1}{4}}={\arcsin \left(\frac{\lambda}{\pi d}\ {\arccos \left(\frac{1}{\sqrt{4}}\right)\ }\right)\ }=3.01\times {10}^{-3}\ {\rm rad}\]
Substituting it into the relation $y=D\,{\tan \theta\ }$, we get
\[y_{\frac{1}{4}}=D\,{\tan \theta_{\frac{1}{4}}\ }=9.04\ {\rm mm}\]
The picture below shows the unpolarized light incident from the left upon a pair of 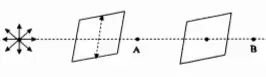 polarizes. The intensity of the unpolarized light is $15\,\rm W/m^2$. The vertical dashed line in the left polarizer shows its transmission axis (TA).
polarizes. The intensity of the unpolarized light is $15\,\rm W/m^2$. The vertical dashed line in the left polarizer shows its transmission axis (TA).
(a) What is the intensity of the light as it passes point A?
(b) After passing point A, the light now passes through a second polarizer, and then passes point B. At B the light's intensity is $3\,\rm W/m^2$. What is the smallest angle between the directions of the TA's of the two polarizers?
(a) Note: when an unpolarized light passes through a polarizer, the intensity of the transmitted light is exactly half that of the incident wave. So $I_A=\frac{I_0}{2}=\frac{15}{2}=7.5\ {\rm W/}{{\rm m}}^{{\rm 2}}$
(b) When polarized light passes through a polarizer (analyzer), the intensity of the transmitted light is $I=I_0{{\cos }^2\phi\ }$, where $\phi$ is the angle between the polarization direction of the incident light and the polarizing axis of the polarizer (Malus's law). So
\begin{align*} I_B&=I_A\,{{\cos }^2 \phi} \\ 3&=7.5\,{{\cos}^2 \phi}\\ \Rightarrow {{\cos}^2 \phi}&=0.4\\ \Rightarrow \ {\cos\phi}&=\pm 0.633 \end{align*}
Therefore, we the angle is \[\phi=50.8{}^\circ \]
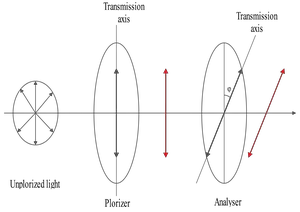
In a Young's double-slit experiment ($d=0.2\,{\rm mm}$) coherent light from 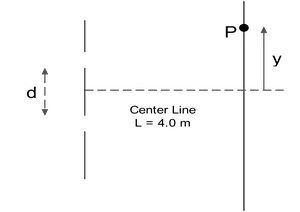 two sources $\lambda_1=450\,{\rm nm}$ and $\lambda_2=600\,{\rm nm}$ illuminate the double slit (see figure). There is a point P on the screen, a distance $y$ up from the centerline at which a maximum from $\lambda_1$ overlaps a minimum from $\lambda_2$. This point P is the closest such point to the centerline for the described overlapping.
two sources $\lambda_1=450\,{\rm nm}$ and $\lambda_2=600\,{\rm nm}$ illuminate the double slit (see figure). There is a point P on the screen, a distance $y$ up from the centerline at which a maximum from $\lambda_1$ overlaps a minimum from $\lambda_2$. This point P is the closest such point to the centerline for the described overlapping.
(a) What is the position $y$ at which this overlapping occurs?
(b) Counting the central bright fringe as the first bright fringe ($0$${}^{th}$ order bright fringe) and the first dark fringe above the centerline ($0$${}^{th}$ order dark fringe) as the first dark fringe, then at the position P which bright fringe is overlapping which dark fringe?
(a) Maximum and minimum are instructive and destructive points, respectively.
$d\,{\sin \theta\ }=m\lambda\ $for instructive and $d\,{\sin \theta\ }=\left(m+\frac{1}{2}\right)\lambda$ for destructive where $m=0,1,2,\dots $
\[\left. \begin{array}{lccr} {\rm For\ }\lambda_1 : & d\,\sin \theta=m_1\lambda_1\ &, \ max \\ {\rm For\ }\lambda_2\: & d\,{\sin \theta\ }=\left(m_2+\frac{1}{2}\right)\lambda_2\ &,\ min \end{array} \right\}\Rightarrow m_1\lambda_1=\left(m_2+\frac{1}{2}\right)\lambda_2\]
$$\to \frac{\lambda_1}{\lambda_2}=\frac{m_2+\frac{1}{2}}{m_1}$$ where $m_1 , m_2$ are integers.
\begin{gather*} \frac{450}{600}=\frac{\lambda_1}{\lambda_2}=\frac{m_2+\frac{1}{2}}{m_1}\\ \\ \Rightarrow \frac{3}{4}=\frac{2m_2+1}{2m_1}\to \left\{ \begin{array}{c}2m_1=4\to m_1=2 \\ 2m_2+1=3\to m_2=1 \end{array}\right.\end{gather*} Bright fringes are located at $y_m=L\,{\tan \theta_m\ }$ or $y_m=L\frac{m\lambda}{d}$.\[y_m=L\frac{m\lambda}{d}=\left\{ \begin{array}{lcr}L\displaystyle{\frac{m_1 \lambda_1}{d}}=4\frac{2\times 450}{0.2\times {10}^{-3}}=0.018\,{\rm m=1.8\ cm} \\ \\ \displaystyle{L\frac{\left(m_2+\frac{1}{2}\right)\lambda_2}{d}}=4\frac{\left(1+\frac{1}{2}\right)\times 600}{0.2\times {10}^{-3}}=0.018\ {\rm m}=1.8\ {\rm cm} \end{array}\right.\]
As expected!
(b) $\left. \begin{array}{c} m_1=2\to 3^{nd}\ bright\ fringe \\ m_2=1\ \to 2^{nd}\ dark\ fringe \end{array}\right\}$
Two thin parallel slits that are $0.0116\,{\rm mm}$ apart are illuminated by a laser beam of wavelength $585\,{\rm nm}$. The resulting interference pattern is presented on a very large distant screen.
(a) What is the largest value of ${\sin \theta\ }$ that we have to consider?
(b) What is the total number of bright fringes that we have to consider?
(c) At what angle relative to the original beam direction will the most distant fringe appear?
(a) Recall that bright fringes are given by equation $d\,{\sin \theta}=m\lambda\ ,\ m=1,2,\dots $. We know from mathematics that the magnitude of ${\sin \theta}$ is less than or equal one i.e. $\left|{\sin \theta\ }\right|\le 1$. Combine these notes to find the maximum value of the number of bright fringes $m$ \begin{gather*} {\sin \theta}=\frac{m\lambda}{d}\le 1 \\ \\ \Rightarrow \quad m\le \frac{d}{\lambda}=\frac{0.0116\times {10}^{-3}}{585\times {10}^{-9}}=19.8 \\ \\ \Rightarrow \quad m_{largest}=19\end{gather*}
By substituting the largest $m$ in the interference equation, we obtain the largest value of ${\sin \theta\ }$.
\begin{align*} (\sin \theta)_{max}&=\frac{m_{max}\lambda}{d}\\\\&=19\,\frac{(5.85\times {10}^{-7})}{0.0116\times {10}^{-3}}\\ \\&=\pm 0.958\end{align*}
(b) $m_{total}=19$ indicates that on each side of the central fringe there is $19$ bright fringes so \[2\left(19\right)+1\left(central\ fringe\right)=39\]
(c) \begin{align*} {\sin \theta_{19}}&=\frac{m\lambda}{d}\\\\&=19\left(\frac{5.85\times {10}^{-7}}{0.0116\times {10}^{-3}}\right)\\\\&=\pm 0.958 \to \theta\\\\&=73.3{}^\circ \quad \text{most distant fringe}\end{align*} And \begin{align*} {\sin \theta_1}&=\frac{m^{'}\lambda}{d}\\ \\&=1\left(\frac{5.85\times {10}^{-7}}{0.0116\times {10}^{-3}}\right)\\\\ &=2.89{}^\circ \quad \text{most near fringe}\end{align*}
Unpolarized light of intensity $S_0$ is incident from the left on a series of polarizes. The angle between the transmission axes of $P_1$ and $P_2$ is $60{}^\circ $.
(a) In terms of $S_0$, the average intensities at $A$ and $B$ are:
(b) A third polarizer $P_3$ is placed first at $A$ then at $B$.
(i) What must be the angle between the transmission axes of $P_1$ and $P_3$ so that no light reaches when $P_3$ is placed at $A$?
(ii) What must be the angle between the transmission axes of $P_1$ and $P_3$ so that no light emerges to the right of $P_3$ when $P_3$ is placed at $B$?
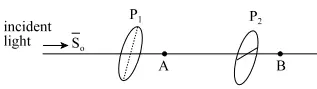
Note: if an unpolarized light with intensity $S_0$ incident on a polarizer then the intensity of the transmitted light is $\frac{S_0}{2}$. This light is polarized so if a second polarizer is placed in front of it then the intensity becomes $S=S_0\,{{\cos }^2 \phi\ }$, where $\phi$ is the angle between polarizing axes of first and second polarizers.
(a) As noted above: $S_A=\frac{S_0}{2}$ and $S_B=S_A\,{{\cos }^2 60{}^\circ \ }=\left(\frac{S_0}{2}\right){\left(\frac{1}{2}\right)}^2=\frac{S_0}{8}$
(b) First $P_3$ is placed in A so the average intensity of light emerges to the right of it is
\[S_A=\frac{S_0}{2}\,{{\cos }^2 \phi^{'}\ }\]
Because we want no intensity after placing $P_3$ therefore $S_A$ must be zero.
\[\frac{S_0}{2}\,{{\cos }^2 \phi^{'}\ }=0\Rightarrow \ \phi^{'}=90{}^\circ \]
Now $P_3$ is placed into B. light passes through two polarizer before incident on it so
\begin{gather*} S_B=\frac{S_0}{8}\,{{\cos }^2 \phi''}=0 \\ \left(no\ light\ transmitted\right) \Rightarrow \ \phi''=90{}^\circ \end{gather*}
Where $\phi^{''}$ is the angle between polarizing axes of $P_3$ and $P_2$. In the other hand, the angle between $P_1$ and $P_2$ is $60{}^\circ $. So the angle between $P_1$ and $P_3$ is $30{}^\circ $.
A suitcase of mass $20\, {\rm kg}$ is hung from two bungee cords. Each cord is stretched $5\, {\rm cm}$ when the suitcase is in equilibrium. If the suitcase is pulled down a little and released, what will be its oscillation frequency?
The two cords produce a pulling upward force of $-kx$, so treat them as one spring with an effective spring constant $k$.
At equilibrium, the force of the cords is equal to the force of gravity \[\Sigma F_y=0\Rightarrow mg=kx\Rightarrow k=\frac{mg}{x}\ \ ,\ \ (*)\]
We know that the frequency of a body with mass $m$ that undergoes a simple harmonic motion is $f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\ \sqrt{\frac{k}{m}}$. So using (*)
\begin{align*} f=\frac{1}{2\pi}\ \sqrt{\frac{k}{m}}&=\frac{1}{2\pi}\ \sqrt{\frac{\frac{mg}{x}}{m}}\\\\ &=\frac{1}{2\pi}\sqrt{\frac{g}{x}}\\\\ &=\frac{1}{2\pi}\sqrt{\frac{9.8}{0.05}}\\\\&=2.2\quad {\rm Hz}\end{align*}
A $0.120\,{\rm kg}$ block is suspended from a spring. When a small pebble of mass $30\,{\rm g}$ is placed on the block, the spring stretches an additional $5.0\,{\rm cm}$. With the pebble on the block, the block oscillates with an amplitude of $12\,{\rm cm}$.
(a) What is the frequency of the motion?
(b) How long does the block take to travel from its lowest point to its highest point?
(c) What is the net force on the pebble when it is at the point of maximum upward displacement?
(a) First determine the spring constant:
Without the pebble, the block and spring is in a mechanical equilibrium (motionless in $y$ direction) so
\[\Sigma F_y=0 \ \to \ m_Bg=kx_1\] But the displacement of the spring ($x$) in this case is not given. When the pebble is placed on the block, instantaneously a new equilibrium position created, so $k\left(x_1+x_2\right)=\left(m_B+m_p\right)g$, where $x_1$and $x_2$ are indicated in the figure below.
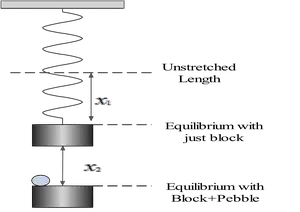
From the two relations above, we conclude that \begin{gather*} k\left(x_1+x_2\right)=\left(m_B+m_p\right)g \\ m_Bg=kx_1\\\\ \Rightarrow m_Bg+kx_2=\left(m_B+m_p\right)g\\\\ \Rightarrow k=\frac{m_pg}{x_2} \end{gather*} Therefore, we have \[k=\frac{0.030\times 9.8}{0.05}=5.88\frac{{\rm N}}{\rm m}\]
Frequency of oscillation is \begin{align*} f&=\frac{1}{2\pi}\omega =\frac{1}{2\pi}\sqrt{\frac{k}{m_{tot}}}\\\\&=\frac{1}{2\pi}\sqrt{\frac{5.88}{0.030+0.120}}\\\\ &\approx 1\quad {\rm Hz} \end{align*}
(b) Traveling from its lowest point to highest point is half of a period. Period of a oscillation is related to the frequency by $T=\frac{1}{f}\approx 1{\rm s}$, therefore the required time is $0.5\,{\rm s}$.
(c) From Newton's 2${}^{nd}$ law $F_{net}=ma$, we must find the acceleration of a simple harmonic motion (SHO) for pebble. Recall that in SHO we have the following relations: \begin{align*} x=A{\cos (\omega t+\alpha)\ }\ \ &,\ \ {\rm displacement\ in\ SHO} \\v=\frac{dx}{dt}=-A\omega\,{\sin \left(\omega t+\alpha\right)\ }\ &,\ \ {\rm velocity} \\ a=\frac{d^2x}{dt^2}=-A\omega^2\,{\cos \left(\omega t+\alpha\right)\ }\ \ &,\ \ {\rm acceleration}\end{align*} In the relations above, if we substitute the $\left|{\sin \left(\omega t+a\right)\ }\ or\ {\cos \left(\omega t+a\right)\ }\right|\le 1$ then we get the maximum values of $x,v$ and $a$. i.e.
$$x_{max}=A\ ,\ v_{max}=A\omega\ ,\ a_{max}=A\,\omega^2$$
Note: $A$ is the amplitude of the oscillation So
\begin{align*} F_{net}=m_pa_{max}=m\,A\,\omega^2&=mA\sqrt{\frac{k}{m_{tot}}}\\ &=\left(0.030\right)\left(0.12\right)\left(39.2\right)\\&=0.141\quad {\rm N} \end{align*}
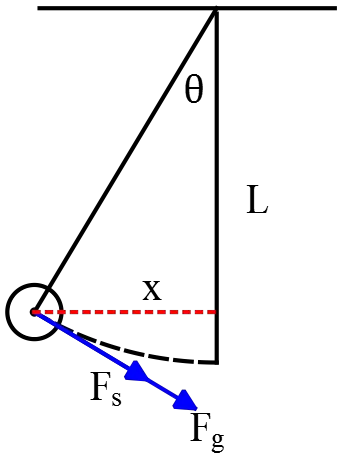
The figure shows a pendulum of length $L$ with a bob of mass $M$. The bob is 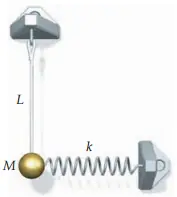 attached to a spring that has a force constant $k$. When the bob is directly below the pendulum support, the spring is unstressed.
attached to a spring that has a force constant $k$. When the bob is directly below the pendulum support, the spring is unstressed.
(a) Derive an expression for the period of this oscillating system for small-amplitude vibrations.
(b) Suppose that $M=1.00\,{\rm kg}$ and $L$ is such that in the absence of the spring the period is $2.00\,{\rm s}$. What is the force constant $k$ if the period of the oscillating system is $1.00\,{\rm s}$?
Now apply Newton's second law to the bob: $\Sigma F=Ma$ \begin{align*} F_s+F_g&=M\frac{d^2x}{dt^2}\\\\-Mg\,{\sin \theta}-kx&=M\frac{d^2x}{dt^2}\end{align*}
But from the figure: ${\sin\theta}=x/L$. Therefore \begin{align*} -Mg\left(\frac{x}{L}\right)-kx&=M\frac{d^2x}{dt^2}\\\\\Rightarrow \quad -\left(\frac{g}{L}+\frac{k}{M}\right)x&=\frac{d^2x}{dt^2}\end{align*}
The above equation is similar to the equation of simple harmonic motion (SHM) i.e. $\frac{d^2x}{dt^2}+\omega^2x=0$, where $\omega$ is the angular frequency of the system. So
\[\omega^2=\frac{g}{L}+\frac{k}{M}\]
(b) First, find the length of the pendulum. In the absence of the spring $T=2\,{\rm s}$, so
\begin{gather*} \left\{\begin{array}{rcl}\omega=\frac{2\pi}{T} &=& \frac{2\pi}{2}=\pi\\\\ k&=&0 \end{array}\right. \\\\ \Rightarrow \omega=\sqrt{\frac{g}{L}}\Rightarrow L=\frac{g}{\pi^2}\end{gather*}
Since the length of the pendulum does not change after placing the spring so substitute $L$ into the angular frequency of the pendulum + spring system and solve for $k$.
\begin{gather*} \omega=\frac{2\pi}{1}=\sqrt{\frac{g}{L}+\frac{k}{M}}\\\\ \Rightarrow {\left(2\pi\right)}^2=\pi^2+\frac{k}{M} \\\\ \Rightarrow k=3\pi^2M=3\pi^2\left(1\right)=29.6\ {\rm N/m} \end{gather*}
More related articles:
Simple pendulum Problems and formula
Harmonic motion Problems with formula
A child's spring toy consists of a $250\ {\rm g}$ plastic frog which bounces up and down on a spring. When the frog is pushed down by $1.5\,{\rm cm}$ below its equilibrium position and released, it vibrates up and down at a frequency of $2.0$ times per second.
(a) Find the spring constant $k$ of the spring.
(b) Assuming no friction, what is the total energy of the bouncing frog?
(c) Find the velocity of the frog when it passes through the equilibrium position (where $x=0$)
(a) The period of an object with mass $m$ under simple harmonic motion with spring constant $k$ is given by
\[T=\frac{1}{f}=2\pi\sqrt{\frac{m}{k}}\]
Where $f$ is the frequency of motion. So \[k=4\,\pi^2f^2m=4\pi^2{\left(2.0\right)}^2\left(0.250\right)=39.5\frac{{\rm N}}{{\rm m}}\]
(b) Because there is no friction so mechanical energy is conserved, i.e., it is a constant of motion.
Note: In an SHO, the total mechanical energy is proportional to the square of the amplitude, i.e.,
\begin{gather*} E_{tot}=\frac{1}{2}mv^2+U=\frac{1}{2}kA^2 \\\\ =\frac{1}{2}kA^2=\frac{1}{2}(39.5){\left(1.5\times {10}^{-2}\right)}^2=0.0044\,\rm J\end{gather*} For an object at its maximum displacement (amplitude), the total mechanical energy is all the potential energy. Because at this point the velocity of the object is zero.
(c) At the equilibrium position ($x=0$) , the spring is not stretched nor compressed so $U=0$
\[E_{tot}=\frac{1}{2}kA^2=U+K\]
\[0.0044=0+\frac{1}{2}mv^2=\frac{1}{2}\left(0.250\right)v^2\Rightarrow v=0.188\ {\rm m/s}\]
A small sound source has a power of $12\,{\rm W}$. How far away from the sound source can you be and still hear it? Recall the threshold of hearing is $1.00\times {10}^{-12}\,\rm W/m^2$.
Note: the intensity of a sound wave with average power $P_{av}$ at distance $r$ is given by
\[I=\frac{P_{av}}{4pr^2}\]
Solving for $r$, we obtain
\[\Rightarrow r=\sqrt{\frac{P_{av}}{4\pi I}}=\sqrt{\frac{12}{4\pi\times {10}^{-12}}}=9.77\times {10}^5\ {\rm m}\]
A guitar string of length $0.5\, {\rm m}$ and linear mass density of ${\rho }_{string}=8.00\times 10^{-2}\,{\rm \ kg/m}$ is held with a tension of ${\rm 5.00\ \times \ 103\ N}$. It is plucked so as to excite the fundamental frequency alone
(a) What is the velocity of a wave on the string?
(b) What is the wavelength and frequency of the fundamental harmonic?
(c) What is the wavelength of the sound in air?
(a) Recall that the wave speed on the sting with tension $T$ and linear mass density $\mu$ is given by
\[v=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{5\times {10}^3}{8\times {10}^{-2}}\ }=250\frac{{\rm m}}{{\rm s}}\]
(b) For a string fixed at both ends, the standing wave condition is $L=n\frac{\lambda_n}{2}\ $and using the relation $v=\lambda_n f_n$ we can find the frequency of the nth harmonic as $f_n=n\frac{v}{2L}$. So
\[f_n=n\frac{v}{2L}\ ,\ n=1,2,3,\dots \ \ but\ \ n=1\ is\ fundamental\ mode\]
\[f_1=\left(1\right)\frac{v}{2L}=\left(1\right)\frac{250}{2\left(0.5\right)}=250\ {\rm Hz\ \ \ ,\ }{\lambda }_{{\rm 1}}=\frac{v}{f_1}=\frac{250}{250}=1\ {\rm m}\]
(c) Recall that when a wave passing through a medium; its frequency does not change but the wavelength changes. So
\[\lambda_1=\frac{v_{sound}}{f_1}=\frac{343}{250}=1.372\ {\rm m}\]
That is, the wavelength of the fundamental mode in air is greater than the string.
A $0.3\, {\rm g}$ wire is stretched between two points $70\, {\rm cm}$ apart. If the tension in the wire is $600\, {\rm N}$ find the wire's first, second and third harmonics?
As mentioned previously, the frequency of the nth harmonic in an excited string with both ends fixed is given by the $f_n=n\frac{v}{2L}$. Where $v$ is speed of the wave on the string with tension $T$ i.e. $v=\sqrt{\frac{T}{\mu}}$. Therefore, first find the speed of the wave
\[v=\sqrt{\frac{T}{\frac{m}{L}}}=\sqrt{\frac{600}{\frac{0.3\times {10}^{-3}\ {\rm kg}}{{\rm 0.7\ m}}}}=1183.2\frac{{\rm m}}{{\rm s}}\]
\[f_1=\left(1\right)\frac{1183.2}{2\left(0.7\right)}=845\ {\rm Hz\ }\ \ {\rm fundamental\ harmonic\ }\left({\rm n=1}\right)\]
\[f_2=\left(2\right)\frac{1183.2}{2\left(0.7\right)}=1690\ {\rm Hz\ \ \ }{{\rm 2}}^{{\rm nd}}{\rm \ harmonic}\]
\[f_3=\left(3\right)\frac{1183.2}{2\left(0.7\right)}=2535\ {\rm Hz\ }\ {{\rm 3}}^{{\rm nd}}{\rm \ harmonic}\]
If a large horsefly $3.0\, {\rm m}$ away from you makes a noise of $40.0\, {\rm dB}$, what is the noise level of $1000$ flies at that distance?
Note: the sound intensity levels are measured on logarithmic scale as $\beta=10\, {\rm dB}{\log \frac{I}{I_0}\ }$, where $I_0={10}^{-12}\ {\rm W/}{{\rm m}}^{{\rm 2}}$ is the threshold of hearing. First, find the intensity of one fly
\[\beta=10\ {\rm dB}\,{\log \frac{I_0}{I}\ }\Rightarrow 40=10\,{\log \frac{I}{I_0}\ }\Rightarrow \frac{I}{I_0}={10}^4\Rightarrow I_{one}={10}^4I_0\]
The intensity of 1000 flies is 1000 times the intensity of one fly that is $I_{1000}=1000I_{one}={10}^7I_0$
\[\beta_{1000}=10\ {\rm dB}\,{\log \frac{I_{1000}}{I_0}\ }=10\,{\log \frac{{10}^7I_0}{I_0}\ }\Rightarrow \ \beta_{1000}=70\ {\rm dB}\]
A crude approximation of voice production is to consider the breathing passages and mouth to be a resonating tube closed at one end.
(a) What is the fundamental frequency if the tube is $0.240\, {\rm m}$ long?
(b) What would the frequency become if the person replaced the air with helium?
($k=1.38\times {10}^{-23}\ {\rm J/K}$, $m_{He}=3.32\times {10}^{-27}{\rm kg}$, air temperature $37{\rm{}^\circ\!\,C}$ , $\gamma=1.4$)
(a) If on end of a tube with length $L$ is fixed (closed), then the condition of the standing waves states that the frequency of nth harmonic is $f_n=nv/4L$. So
\[f_1=\left(1\right)\frac{343}{4\left(0.240\right)}=357.29\, {\rm Hz}\]
(b) The speed of sound waves in the gasses is given by $v=\sqrt{\frac{\gamma kT}{m}}$, where $T$ is the absolute temperature measured in Kelvins (${\rm K}$) and $m$ is the mass of a molecule of the gas. Therefore, first find the speed of the sound in the helium then calculate the fundamental frequency in it.
\[v=\sqrt{\frac{\gamma RT}{M}}=\sqrt{(1.4)(\frac{\left(1.38\times {10}^{-23}\right)\left(273+37{\rm{}^\circ\!\,C}\right)}{3.32\times {10}^{-27}}}=1342.12\frac{{\rm m}}{{\rm s}}\]
\[f^{'}_1=n\ \frac{v}{4L}=\left(1\right)\frac{1342.12}{4\left(0.240\right)}=1399.1{\rm Hz}\ \]
A violin string with a mass of $0.5\, {\rm g}$ and a length of $35\, {\rm cm}$ produces a fundamental frequency of $440\, {\rm Hz}$ when bowed.
(a) What is the tension in the string?
(b) If an observer moves toward the violin at a speed of $20\, {\rm m/s}$, what frequency is heard?
(c) If the sound intensity is $60\, {\rm dB}$ at a distance of $5\, {\rm m}$ from the violin, what acoustical power does the violin produce, assuming it radiates equally in all directions?
(a) If both ends of a string with length $L$ are fixed, then the frequency of the nth harmonic wave is determined by $f_n=n\frac{v}{2L}$, where $v$ is the speed of the wave on the string with tension $T$ and is found by $v=\sqrt{\frac{T}{\frac{m}{L}}}$. Therefore,
\begin{align*} 2L f_n&=n\sqrt{\frac{T}{\frac{m}{L}}} \\\\ \Rightarrow T&=\frac{4Lf^2_nm}{n^2}\\\\&=\frac{4(0.35)(440)^2 (0.5\times {10}^{-3})}{1^2}\\\\&=136\quad {\rm N}\end{align*}
(b) First draw a vector from the receiver toward the source then choose the signs of the Doppler formula as follows (choose plus if any velocity is in the direction of this vector and vice versa).
\begin{align*}f_r&=f_s\frac{v\pm v_r}{v\pm v_s}\\\\&=f_s\frac{v+v_r}{v}\\\\&=440\frac{343+20}{343}\\\\&=465.6\quad {\rm Hz} \end{align*}
(c) The intensity level of the sound is measured as $\beta=10\,{\log \frac{I}{I_0}}$, where $I$ is the intensity of the source of the sound at distance $r$ from it and is given by $I=\frac{P}{4\pi r^2}$ so by combining these equations we get
\begin{gather*}\beta=10\,{\log \frac{P}{{4\pi r^2I}_0}}\\\\ \Rightarrow \frac{P}{{4\pi r^2I}_0}={10}^{\frac{\beta}{10}}\\\\ \Rightarrow P=4\pi r^2I_0\times {10}^{\frac{\beta}{10}}\end{gather*}
Where $I_0={10}^{-12}\, {\rm W/m^{2}}$ is the threshold of hearing. Therefore,
\begin{align*} P&=4\pi\times 5^2\times {10}^{-12}\times {10}^{\frac{60}{10}}\\\\&=314.15\times {10}^{-6}\quad {\rm W}\\\\&=314.15\quad {\rm \mu W}\end{align*}
Twenty violins playing simultaneously with the same intensity combine to give an intensity level of $82.5\, {\rm dB}$.
a) What is the intensity level of each violin?
b) If the number of the violins is increased to 40, will the combined intensity level be more than, less than, or equal to $165\, {\rm dB}$?
(a) The intensity of 20 violins is $20$ times the intensity of one violin, i.e., $I_{20}=20\,I_1$, so use the relation of the intensity level to find $I_{20}$
\begin{gather*} \beta_{20}=10\,{\log \frac{I_{20}}{I_0}\ }\\ \\ \Rightarrow 82.5=10\,{\log\left(\frac{I_{20}}{I_0}\right)}\\\\\Rightarrow I_{20}={10}^{8.25}I_0\end{gather*} Hence, \[I_{20}=20\,I_1\Rightarrow I_1=\frac{{10}^{8.25}}{20}I_0\]
Now compute the intensity level for one violin as
\begin{gather*} \beta_1=10\,{\log \frac{I_1}{I_0}}\\ \\ \to \beta_1=10\,{\log \left(\frac{{10}^{8.25}}{20}\right)}=69.48\quad {\rm dB}\end{gather*}
(b) As before, $I_{40}=40I_1$. Therefore, \begin{align*} I_{40}&=10\,{\log \left(\frac{I_{40}}{I_0}\right)}\\\\&=10\,{\log \left(\frac{40\times\frac{{10}^{8.25}}{20}I_0}{I_0}\right)}\\\\&=85.5\ {\rm dB<165\ dB}\end{align*} You can find more problems on sound intensity level here.
Your are trying to understand important instructions from someone who is soft-spoken. From your distance $r_1$ her voice sounds like an average whisper of $20\, {\rm dB}$. So you move to a position where you are a distance $r_2$ from her and the sound level is at $60\, {\rm dB}$.
(a) If the intensity is $I_1$ at distance $r_1$ and $I_2$ at distance $r_2$, calculate the ratio $I_2/I_1$.
(b) Use your answer to part (a) to calculate the ratio $r_2/r_1$.
(a) The intensity level ($\beta$) of the sound waves is measured in ${\rm dB}$ by the following equation
\[\beta=10\,{\log \frac{I}{I_0}\ }\]
Where $I$ is the intensity of the source of sound at distance $r$ and $I_0$ is the hearing threshold. So find the ratio $I_2/I_1$ as follows
\[\beta_1=10\,{\log \frac{I_1}{I_0}\ }\Rightarrow 20=10\,{\log \frac{I_1}{I_0}\ }\Rightarrow \frac{I_1}{I_0}={10}^2\]
\[\beta_2=10\,{\log \frac{I_2}{I_0}\ }\Rightarrow 60=10\,{\log \frac{I_2}{I_0}\ }\Rightarrow \frac{I_2}{I_0}={10}^6\]
We have used the definition of the logarithm i.e. $y={\log x\ }\Rightarrow x={10}^y$. Dividing the two relation, we obtain
\[\frac{I_2}{I_1}=\frac{{10}^6}{{10}^2}={10}^4\]
(b) The sound intensity $I$ is defined as the sound power $P$ that passes perpendicularly through a surface divided by the area $A$ of that surface $I=P/A$. For a point source at distance $r$ it is $I=P/4\pi r^2$ so
\[I_1=\frac{P}{4\pi r^2_1}\ \ and\ \ I_2=\frac{P}{4\pi r^2_2}\]
Dividing the two equation, gives
\[\frac{r_1}{r_2}={\left(\frac{I_2}{I_1}\right)}^{\frac{1}{2}}={\left({10}^4\right)}^{\frac{1}{2}}=100\ \]
Therefore, $$\frac{r_2}{r_1}=\frac{1}{100}=0.01$$
An open organ pipe (open at both ends) has a harmonic with frequency of $440\, {\rm Hz}$. The next higher harmonic in the pipe has a frequency of $528\, {\rm Hz}$.
(a) Find the frequency of the fundamental.
(b) What is the length of the pipe?
(a) If the both ends of a tube is open then the frequency of the $n$th harmonic is given by the $f_n=n\frac{v}{2L}\ ,\ n=1,2,3,\dots $ . Consider the $nt$h frequency is $440\, {\rm Hz}$, the next frequency is $\left(n+1\right)$th. Therefore,
\[f_n=n\frac{v}{2L}=440\ {\rm Hz\ ,\ \ }f_{n+1}=\left(n+1\right)\frac{v}{2L}=528\ {\rm Hz}\]
Subtracting them, we obtain
\[f_{n+1}-f_n=528-440\to \frac{v}{2L}=88\]
Now use the above result to find the fundamental frequency $f_1=\left(1\right)\frac{v}{2L}=88\ {\rm Hz}$
(b) Let the speed of the sound be $v=343\, {\rm m/s\ }$, therefore,
\[\frac{v}{2L}=88\Rightarrow l=\frac{343}{2\left(88\right)}=1.94\ {\rm m}\]
A guitar string has a tension $100\, {\rm N\ }$ and has a mass of $7.0\, {\rm g}$ and is $0.45\, {\rm m}$ long.
(a) What is the speed of a wave on this string?
(b) What is the frequency of the third harmonic on this string?
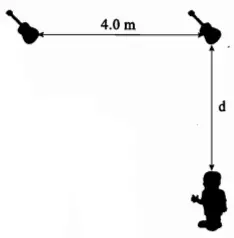
(c) Two identical guitars, as described above, play a note in phase at their fundamental frequencies. If the guitars and a listener are positioned as shown in the drawing, what is the largest possible $d$, such that the listener hears no sound?
(a) The speed of the waves on a string with tension $T$ and mass density $\mu=m/L$ is given by
\[v=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{100}{\frac{0.007}{0.45}}}=80.17\, \frac{{\rm m}}{{\rm s}}\]
(b) Since both ends of a guitar string is fixed so the frequency of the nth harmonic is found by
\[f_n=n\frac{v}{2L}=\left(3\right)\frac{80.17}{2\left(0.45\right)}=267.23\ {\rm Hz}\]
(c) First, compute the fundamental frequency of the string and associated 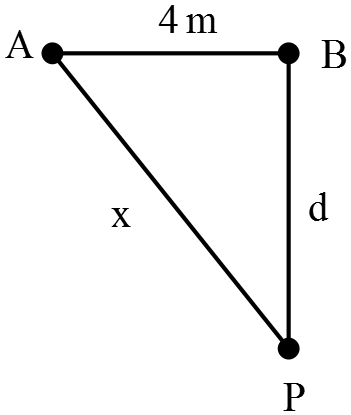 wavelength in the air
wavelength in the air
\[f_1=\left(1\right)\frac{v}{2L}=\left(1\right)\frac{80.17}{2\left(0.45\right)}=89.07\ {\rm Hz}\]
\[\lambda_1=\frac{v_{sound}}{f_1}=\frac{343}{89.07}=3.85\ {\rm m}\]
Listener hears no sound means that at the location of listener the waves must be destructive! Therefore, use the destructive interference pattern in waves that is the path difference of waves must be equal the half integer of wavelength i.e. $\Delta =n\lambda\ ,\ \ n=\frac{1}{2},\frac{3}{2},\dots $
\[\Delta =x-d=n\lambda \Rightarrow x=\left(d+n\lambda \right)\]
squaring both sides, we obtain
\[x^2={\left(d+n\lambda\right)}^2=d^2+n^2\lambda^2+2n\lambda d\]
Now as shown in the figure, use the Pythagorean theorem to write $x^2=d^2+4^2$. Substitute this into the relation above
\[d^2+16=d^2+{\left(n\lambda\right)}^2+2\left(n\lambda\right)d\Rightarrow d=\frac{16-{\left(n\lambda\right)}^2}{2\left(n\lambda\right)}\]
\[d=\frac{16-{\left(\frac{1}{2}\lambda\right)}^2}{2\left(\frac{1}{2}\lambda\right)}=\frac{16-\frac{{\left(3.85\right)}^2}{4}}{3.85}=3.19\ {\rm m}\]
If $n=3/2\ $then $d=1.50$ so the largest value of $d$ is $3.19\ {\rm m}$.
A train and a car are traveling in the same direction. The train's speed is $22.5\, {\rm m/s}$ and the car's speed is $9.5\, {\rm m/s}$. Assume the speed of the sound in air is $343\, {\rm m/s\ }$. if the train blows its whistle ($f=1500.0\, {\rm Hz}$), what is the frequency passengers in the car hear when:
(a) The train is approaching from behind the car.
(b) The train is moving away in front of the car.
Apply the Doppler shift equation as
\[f_r=f_s\frac{v\pm u_r}{v\pm u_s}\]
Where $f_r$ and $f_s$ are the frequencies of the receiver and source and also $u_r\ ,\ u_s$ are the receiver and source velocities, respectively.
Important note about signs in the Doppler shift: First, suppose a direction from receiver toward the source then all velocities in the direction of this vector are positive and all velocities in opposite direction are negative.
In this problem car is the receiver and train is the source of sound. Using these notes, we have: $v=343\, {\rm m/s}$ , $f_s=1500\, {\rm Hz\ ,\ }u_r=9.5\, {\rm m/s}$ , $u_s=22.5\, {\rm m/s}$ , $f_r=?$
(a) The figure below shows the situation:
\[f_r=f_s\frac{v-u_r}{v-u_s}=1500\frac{343-9.5}{343-22.5}=1560.8\ {\rm Hz}\]

(b) Our sketch for this case is as follows:
\[f_r=f_S\frac{v+u_r}{v+u_s}=1500\frac{343+9.5}{343+22.5}=1446.6\ {\rm Hz}\]

A carousel is $5.00\, {\rm m}$ in radius and has a pair of $750\, {\rm Hz}$ sirens mounted on posts at the opposite ends of a diameter. The carousel rotates with an angular velocity of $0.800\, {\rm rad/s}$. A stationary listener is located at a distance from the carousel. The speed of the sound is $343\, {\rm m/s}$. What is the longest wavelength reaching the listener from the sirens?
As shown in the figure, there are two velocities with respect to the listener. First, use the relation $v=r\omega$ to find the velocity of the source then apply Doppler Effect to calculate the frequencies associated with these sources.
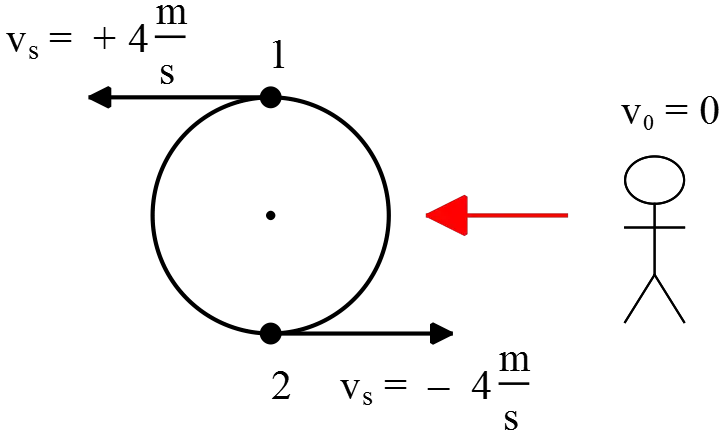
\[v_s=r\omega=5\times 0.8=4\frac{{\rm m}}{{\rm s}}\]
To use the Doppler Effect, as previously mentioned, draw a vector from the listener to the source then compare the signs of velocities in the Doppler equation with this vector.
\[f_o=f_s\frac{v\pm u_o}{v\pm u_s}\]
\begin{align*} \text{Case one:} \quad f_o&=f_s \left(\frac{v}{v+u_s}\right) \\\\ &=750\left(\frac{343}{343+4}\right) \\\\ &=741.35\, {\rm Hz} \\\\ \text{Case two:} \qquad \ f_o&=f_s\left(\frac{v}{v-u_s}\right)\\\\ &=750\left(\frac{343}{343-4}\right)\\\\ &=758.84\ {\rm Hz} \end{align*}
Now with the given frequencies find the associated wavelengths of them as
Case one: \[\lambda_1=\frac{v}{f_o}=\frac{343}{741.35}=0.462\, {\rm m}=46.2\ {\rm cm}\]
Case two: \[\lambda_2=\frac{v}{f^{'}_o}=\frac{343}{758.84}=0.452\, {\rm m}=45.2\ {\rm cm}\]
So the longest wavelength is $46.2\, {\rm cm}$.
A whistling train is moving with a velocity of $v_{train}= 25\, {\rm m/s}$ towards a station. The frequency of the train whistle is $500\,{\rm Hz}$.
a) Compute the frequency of the sound heard by a passenger on the platform in the station.
b) The sound of the whistling train is reflected by a nearby mountain and the reflected sound is heard by the train conductor. If the train moves towards the mountain with the same speed $v_{train}= 25\, {\rm m/s}$ as given above, what is the frequency of the reflected sound as heard by the train conductor?
c) What is the beat frequency between the emitted and reflected sound as heard by the train conductor?
(a) Use the Doppler Effect. To do this First draw a vector from the receiver toward the source and then find the signs of the velocities with respect to this vector.
\[f_r=f_s\frac{v\pm u_r}{v\pm u_s}=f_s\frac{v}{v-u_s}=500\frac{343}{343-25}=539.3\ {\rm Hz}\]

(b) In this case, the mountain is as source with the reflected frequency $539.6\, {\rm Hz\ }$and the train conductor is receiver. So the frequency that conductor receives is
\[f_{train}=f_{moun}\frac{v\pm u_{train}}{v\pm u_{moun}}=f_{moun}\frac{v+u_{train}}{v}=539.3\frac{343+25}{343}=578.6\ {\rm Hz}\]

(c) By definition, beat frequency is the difference of two frequencies:
\[f_{beat}=\Delta f=f_{train}-f_{whistle}=978.6-500=78.6\ {\rm Hz}\]
Two eagles fly directly toward one another, the first at $15\, {\rm m/s}$ and the second at $20\, {\rm m/s}$. Both birds screech, one emitting a frequency of $3200\, {\rm Hz}$ and the other at $3800\, {\rm Hz}$. What frequency do they receive if the speed of the sound is $330\, {\rm m/s}$?
Use the Doppler Effect for each of them. The received frequency by the eagle $1$ is \begin{align*} f_{O_1}&=f_{S_2}\frac{v\pm u_{O_1}}{v\pm u_{S_2}} \\\\ &=(3800) \frac{330+15}{330-20}\\\\ &=4229\quad \rm Hz\end{align*} In the case of eagle $2$, the eagle $1$ is a source and eagle $2$ is a receiver (or object). Thus, the frequency perceived by the eagle $2$ is found to be \begin{align*} f_{O_2}&=f_{S_1}\frac{v\pm u_{O_2}}{v\pm u_{S_1}}\\\\ &=(3200) \frac{330+20}{330-15} \\\\ &=3556\quad \rm Hz\end{align*} Practice more on the Doppler effect problems.
An ambulance is traveling with its siren on. Initially you are standing still and observe a frequency of $0.9$ times the frequency as compared to what the driver of the ambulance hears. $v_{sound}=343\, {\rm m/s\ }$.
(a) Is the ambulance moving towards you or away from you?
(b) What is the speed of the ambulance?
(c) You later begin to run in the opposite direction as the ambulance at a speed of $3.0\, {\rm m/s\ }$. What frequency do you hear if the siren has a frequency of $900\, {\rm Hz}$?
a) Here ambulance is the source and the standing person is the receiver (object) since $f_o=0.9\,f_s$, so the ambulance moves away from the observer (you).
b) Use the Doppler Effect to find the speed of the ambulance.
\begin{gather*} f_s=f_o\frac{v\pm u_s}{v\pm u_o}\\\\ \Rightarrow f_s=f_o\ \left(\frac{v+u_s}{v}\right) \\\\ \Rightarrow \ f_s=0.9f_s\,\left(\frac{343+u_s}{343\ }\right) \\\\ \Rightarrow \boxed{u_s=38.11\, {\rm m/s}}\end{gather*}
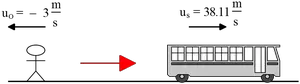
c) Given data: $u_o=3\, {\rm m/s}$, $u_s=38.11\, {\rm m/s}$, $f_s=900\, {\rm Hz}$ , $f_o=?$ As shown in the figure we have
\begin{align*} f_o&=f_s\frac{v\pm u_o}{v\pm u_s} \\\\ &=f_s\frac{v-u_o}{v+u_s} \\\\ \Rightarrow f_o &=900\frac{343-3}{343+38.11} \\\\ &=802.9\ {\rm Hz}\end{align*}
The sound source of a ship's sonar system operates at a frequency of $22.0\,{\rm kHz}$. the speed of the sound in water (assumed to be at a uniform $20{\rm{}^\circ\!\,C}$) is $1482\, {\rm m/s}$.
a) What is the wavelength of the waves emitted by the source?
b) What is the difference in frequency between the directly radiated waves and the waves reflected from a whale traveling directly toward the ship at $4.95\ {\rm m/s.}$ the ship is at rest in the water.
(a) The wavelength emitted from a source is related to the frequency by
\[\lambda=\frac{v}{f}=\frac{1482}{22\times {10}^3}=0.0673\,{\rm m}\]
(b) In first case, the sonar is source and the whale is receiver (object) so the frequency that the whale perceives is:
\[f_w=f_s\frac{v+u_w}{v+u_s}=\left(22\times {10}^3\right)\left(\frac{1482+4.95}{1482+0}\right)=22073.4\,{\rm Hz} = 22.073\,{\rm kHz}\]

In second case, the reflected frequency from whale (in first case) is source and the sonar is receiver (object). Thus the frequency that the sonar received is
\[f_s=f_w\frac{v+u_s}{v+u_w}=22.073\ \left(\frac{1482}{1482-4.95}\right)=22.17\times {10}^3\ {\rm Hz}\]

\[\Delta f=22.17-22.073=0.097{\rm kHz}\]
In a large tank, two tiny underwater speakers of radius $r=1.1\times {10}^{-3}\,{\rm m}$ are placed next to each other. The speakers vibrate at $1.2\, {\rm kHz}$ with the same amplitude (they are like vibrating beats). A microphone at the bottom of the tank records the superposition of sound from the two speakers. The mass of each speaker is $0.015\,{\rm g}$. the adiabatic bulk modulus of water is $B=2.2\times {10}^9\, {\rm N/m^2}$
a) What is the velocity of sound in the water?
b) What is the wavelength of the sound in the water?
c) One of the speakers is dropped and glides towards the bottom of the tank at a constant velocity, while still emitting sound waves, what is the beat frequency recorded by the microphone? (you may model the speakers as spheres and assume the amplitude of the wave from each speaker is the same at the microphone)
(a) The speed of waves in fluids such as air or water is given by $v=\sqrt{\frac{B}{\rho}}$ where B is the Bulk modulus and $\rho$ is the density of the medium. Therefore
\[v=\sqrt{\frac{B}{\rho}}=\sqrt{\frac{2.2\times {10}^9}{1000}}=1483\, {\rm m/s}\]
(b) Having the sound speed in the water $v$, we can find its wavelength by
\[\lambda=\frac{v}{f}=\frac{1483}{1200}=1.24\ {\rm m}\]
(c) Fluids exerts a drag force on small, slowly moving spheres by stock's law as $F_d=6\pi \eta rv$. In addition to the drag force, there is also a buoyancy force. Thus, draw a free body diagram and apply Newton's second law as follows \[\Sigma F_y=ma=0\ \left(const\ velocity\right)\]
\[mg-F_B-F_D=0\]
\[mg=\rho_w\, V_{submerg}\,g+6\pi\eta rv\] Where $F_B$ is the buoyant force exerted on the body from the fluid surrounding it whose magnitude is obtained using the well-known buoyant force formula.
Solving the above equation for $v$, we have \begin{align*} v&=\frac{mg-\frac{4}{3}\pi r^3\rho_w g}{6\pi\eta r}\\ &=\frac{\left(0.015\times {10}^{-3}\times 9.8-\frac{4}{3}\pi\times {\left(1.1\times {10}^{-3}\right)}^3\left(1000\right)\left(9.8\right)\right)}{2.07\times {10}^{-3}}\\ &=4.46\frac{{\rm m}}{{\rm s}} \end{align*} Now suppose this sinking speaker as a source with velocity $v_s=4.46\, {\rm m/s}$ and the stationary speaker as the receiver (object). Applying Doppler effect and solving for the frequency received by the stationary speaker, we obtain \begin{align*} f_r&=f_s\frac{v\pm u_r}{v\pm u_s}\\\\&=1200\frac{1483+0}{1483+4.46}\\\\&=1196.4\quad {\rm Hz}\end{align*}
This is a frequency that the stationary speaker receives. Recall from the beats frequency problems section, the frequency of beats heard is \[\left|\Delta f\right|=\left|f_r-f\right|=\left|1196.4-1200\right|=3.6\, {\rm Hz}\]
At rest, a car's horn sounds at a frequency of $480\, {\rm Hz}$. The horn is sounded while the car is moving down the street. A bicyclist moving in the same direction with one-third the car's speed hears a frequency of $422\, {\rm Hz}$. What is the speed of the car? ( the speed of sound $v=345\, {\rm m/s}$)
First draw a vector from receiver (bicyclist) to the source of sound (car) and then by using it determine the signs in the Doppler formula as follows
\[f_r=f_s\frac{v\pm v_r}{v\pm v_s}\]
\[f_r=f_s\frac{v+v_r}{v+v_s}\]
Given data are: $f_s=480\ {\rm Hz}$ , $v_r=\frac{1}{3}v_s$ , $f_r=422\ {\rm Hz}$
\[\Rightarrow 422=480\frac{345+\frac{1}{3}v_s}{345+v_s}\]
\[v_s=76.37\,\rm m/s\]
When a certain string is clamped at both ends, the lowest four resonant frequencies are $50$,$100$,$150$, and $200 \mathrm {Hz}$. When the string is also clamped at its midpoint, the lowest four resonant frequencies are:
(a) 50, 100, 150, and 200 Hz
(b) 50, 150, 250, and 300 Hz
(c) 100, 200, 300, and 400 Hz
(d) 25, 50 75, and 100 Hz
(e) 75, 150, 225, and 300 Hz
The waves that are produced in a string with both ends fixed are called standing waves. In this case, the length of the string is equal to some integer multiple of half-wavelengths i.e. $L=n\ \lambda /2$, or its wavelengths are quantized as ${\lambda }_n=2L/n$ where ${\lambda }_n$ is the wavelength of the $n$th mode.
In the other words, a standing wave can exist only if its wavelength satisfies the equation above. The fundamental relation between frequency $f$ and wavelength $\lambda $ of a traveling wave with velocity $v$ is $v=f\lambda $. Therefore, the frequency of $n$th mode is found using the standing wave formula below \[f_n=n\frac{v}{2L}\quad ,\quad \left(n=1,2,3,\dots \right)\]
The frequency of $n=1$ case is called the fundamental frequency i.e. $f_1=\frac{v}{2L}$.
The $50\,{\rm Hz}$ frequency in above is fundamental frequency so using it we can find the ratio of $v/L$ as
\begin{align*} f_1&=\frac{v}{2L}\\\\ 50&=\frac{v}{2L}\\\\\Rightarrow \frac{v}{L}&=100 \end{align*}
Note: The speed of waves in a medium depends on the physical properties of that so in the second stage the speed of waves $v$ no longer changes.
At the second stage, we have a standing wave again with frequencies as $f^{'}_n=n\ v/2L^{'}$. In this case $L^{'}=L/2$. Thus
\[n=1\to f_1=\frac{v}{2L^{'}}=\frac{1}{2}\left(\frac{v}{\frac{L}{2}}\right)=\frac{v}{L}=100\ \mathrm{Hz}\]
\[n=2\to f_2=2\frac{v}{2L^{'}}=\frac{v}{\frac{L}{2}}=2\left(100\right)=200\ \mathrm{Hz}\]
\[n=3\to f_3=3\frac{v}{2L^{'}}=\frac{3}{2}\frac{v}{\frac{L}{2}}=3\left(100\right)=300\ \mathrm{Hz}\]
\[n=4\to f_4=4\frac{v}{2L^{'}}=2\frac{v}{\frac{L}{2}}=4\ \left(100\right)=400\ \mathrm{Hz}\]
The correct answer is C.
A microphone of surface area $2.0\,\rm cm^2$ absorbs $1.1\,\rm mW$ of sound. What is the intensity of sound hitting the microphone?
(a) $2.2\times {10}^{-5}\,\rm W/m^2$
(b) $0.55\,\rm W/m^2$
(c) $2.2\,\rm W/m^2$
(d) $2.8\,\rm W/m^2$
(e) $5.5\,\rm W/m^2$
By definition of the intensity of waves as the ratio of the time rate of energy transported to the unit area we have
\[I=\frac{P}{A}\]
Where $P$ which is the time rate of energy transported is called power of the source. So \[I=\frac{1.1\times {10}^{-3}\,\rm W}{2\times 10^{-4}\,\rm m^2}=5.5\,\rm W/m^2\]
The correct answer is E.
Five organ pipes are described below. Which one has the highest fundamental frequency?
(a) A $2.3\, \mathrm m$ pipe with one end open and the other closed
(b) A $3.3\, \mathrm m$ pipe with one end open and the other closed
(c) A $1.6\, \mathrm m$ pipe with both ends open
(d) A $3.0\, \mathrm m$ pipe with both ends open
(e) A pipe in which the displacement nodes are $5\, \mathrm m$ apart
As mentioned earlier, the normal mode frequencies of strings at different conditions are given by the following equations
\[f_n=n\frac{v}{2L}\left(n=1,2,3,\dots \right)\ \ \ \ \ both\ ends\ fixed\ or\ open\]
\[f_n=n\frac{v}{4L}\left(n=1,3,5,\dots \right)\ \ \ \ \ open\ at\ only\ one\ end\]
In A the length of pipe is $L=2.3\ \mathrm{m}$ and fixed at one end so its normal modes are
\[f_n=n\frac{v}{4L}\to \ \ n=1\ ,\ \ f_1=\frac{v}{4\left(2.3\right)}=\frac{v}{9.2}\]
In B, $L=3.3\ \mathrm{m}$ and its conditions is same as the $A$
\[f_n=n\frac{v}{4L}\to \ \ n=1\ ,\ \ f_1=\frac{v}{4\left(3.3\right)}=\frac{v}{13.2}\]
In C, $L=1.6\ \mathrm{m}$ and closed at both ends,
\[f_n=n\frac{v}{2L}\to \ \ n=1\ \ ,\ \ f_1=\frac{v}{2\left(1.6\right)}=\frac{v}{3.2}\]
In D, $L=3.0\ \mathrm{m}$
\[f_n=n\frac{v}{2L}\to \ \ n=1\ \ ,\ \ f_1=\frac{v}{2\left(3.0\right)}=\frac{v}{6}\]
In E, displacement nodes are $5\ \mathrm{m}$ apart that is the fundamental wavelength of such a pipe is ${\lambda }_1=5\ \mathrm{m}$, using the relation between speed and frequency $f=\frac{v}{\lambda }$, we have
\[f_1=\frac{v}{5}\]
Since the speed of waves on a string depends on its linear mass density and tension on it therefore
The correct answer is C.
A particle with a charge of $5\times {10}^{-6}\mathrm{C}$ and a mass of $\mathrm{20\ g}$ moves uniformly with a speed of $\mathrm{7\ m/s}$ in a circular orbit around a stationary particle with a charge of $-5\times {10}^{-6}\mathrm{C}$. The radius of the orbit is:
(a) $0\ \mathrm{m}$
(b) $0.23\ \mathrm{m}$
(c) $0.62\ \mathrm{m}$
(d) $1.6\ \mathrm{m}$
(e) $4.4\ \mathrm{m}$
In a circular motion there always is a centripetal force toward the center of the circle that in this case is provided by the Coulomb's force between the charges. Using Newton's second law of motion along the radius, we get
\[\Sigma\vec{F}=m\vec{a} \Rightarrow F_e=\frac{mv^2}{r}\] where $F_e$ is Coulomb's force between two charged particles.
\begin{gather*} k\frac{\left|q_1q_2\right|}{r^2}=m\frac{v^2}{r}\\\\ \Rightarrow r=k\frac{\left|q_1q_2\right|}{mv^2}\\\\ =\left(9\times {10}^9\right)\frac{{\left(5\times {10}^{-6}\right)}^2}{\left(20\times {10}^{-3}\right){\left(7\right)}^2}=0.23\quad {\rm m}\end{gather*}
The correct answer is B.
In a Young's double-slit experiment, the slit separation is doubled. To maintain the same fringe spacing on the screen, the screen-to-slit distance $D$ must be changed to:
(a) $D/2$
(b) $D/\sqrt{2}$
(c) $D\sqrt{2}$
(d) $2D$
(e) $4D$
In Young's double-slit experiment, the distance from the centerline to the center of a fringe is given by $y=D\ m\lambda /d$ where $r,m,\lambda $ and $d$ are the screen-to-slit separation, $m$th bright or dark fringe, $\lambda $ the wavelength of the source and $d$ is the distance between slits, respectively.
In the case of bright fringes $m=0,\pm 1,\pm 2,\dots $ and for dark fringes $m=\pm \frac{1}{2},\pm \frac{3}{2},\dots $ .
The distance between two fringe is found by two consecutive $m$th as follows
\begin{align*} \Delta &y=y_{m+1}-y_m \\\\ &=D\frac{(m+1)\lambda}{d}-D\frac{m\lambda}{d} \\\\ &=D\frac{\lambda}{d}\end{align*}
Because the source does not change $\lambda =\lambda'$ so
\begin{gather*} \frac{\Delta y}{\Delta y'}=\frac{D}{D'}\frac{d'}{d} \\\\ 1=\frac{D}{D'}\frac{2d}{d} \\\\ \Rightarrow D'=2D \end{gather*}
The correct answer is D.
Most useful formula in Waves:
Sound wave in an ideal gas: $$v=\sqrt{\frac{\gamma RT}{M}}$$
Open pipe: $f_n=\frac{nv}{2L}$
Closed pipe: $f_n=\frac{nv}{4L}$
Doppler effect:
\[ f_O=f_s\frac{v_O \pm u_O}{v_s \pm u_s}\]
Sound intensity Level: $$\beta=(10\, \rm{dB})\, \rm{\log}\,\frac{I}{1.0 \times 10^{-12} \rm{\frac{W}{m^2}}}$$
The intensity of the light transmitted through the analyzer is (Malus's law):
\[I=I_{max}\cos^2 \phi\]
where $I_{max}$ is the maximum intensity at $\phi=0$ and $I$ is the amount of transmitted light at angle $\phi$.
© 2015 All rights reserved. by Physexams.com
