1. Home
  2. Courses
  3. Electrostatic
  4. Electric Flux: Definition & Solved Examples

Electric Flux: Definition & Solved Examples

Definition of electric flux:

Let us suppose a rectangular loop in direction of flowing water is placed such that the plane of the loop is perpendicular to the flow of water. Let $A$ be the area of the loop and $v$ be the velocity of the water.

In this case, the rate of flow of water through the loop, which is denoted by $\Phi$, is defined as $\Phi=Av$ where $\Phi$ is called the flux. 

If the loop is not perpendicular to the flow of water so that it makes some angle $\theta$ with the flow, in this case, the flow is defined as $\Phi=A\left(v\,\cos\theta\right)$.

This is similar to the electric field. From electrostatic recall that the electric field due to a collection of charges is visualized by some lines which are called the field lines.

On the other hand, any imaginary closed surface has a unit vector perpendicular to it. This unit vector is called the normal vector.

The analogous to electric flux is the magnetic flux which is a measure of how many magnetic field lines pass through a surface.

Unit vectors in Cartesian coordinate are described on the page below with a couple of solved problems
Unit vector solved problems 

The concrete method for finding the flux of electric field through any closed surface is as follows: Once the angle between $\vec E$ and normal vector $\hat n$ to the surface of area $A$ is $\theta$, it is sufficient to multiply the electric field due to the existing A graphical representation of electric fluxfield lines in the closed surface by the area of the surface.

Since the electric field is not uniform across the whole surface so one can divide the surface into infinitesimal parts which are called the area elements $dA$.

Now that the electric field across this infinitesimal element is rather uniform by multiplication of $\vec E$ and $d\vec A$, where $\vec A$ is the vector area of the surface and summing these contributions we can arrive at the definition of electric flux \begin{align*} \Phi_E &\approx \vec E_1 \cdot \Delta \vec A_1+\vec E_2 \cdot \Delta \vec A_2+\cdots+\vec E_n\cdot \Delta\vec A_n\\&=\Sigma\vec E_i\cdot\Delta \vec A_i\end{align*} In the limit of $\Delta A \rightarrow 0$, this discrete and approximate sum goes to a well-defined integral.

The mathematical language is as follows \[\Phi_E=\int_S{\vec E\cdot \hat n d\vec A}=\int_S{\vec E\cdot d\vec A}\] Dot denotes the scalar product of the two quantities.

The right-hand side of the above, which is called the surface integral, in cases that the desired surface and/or electric field varies arbitrarily is a hard task to compute.

The calculation is straightforward when the charge distribution is totally symmetric since in this case, one can choose simply a suitable surface.

Summary:

The number of electric field lines that pass through any closed surface is called the electric flux which is a scalar quantity.

Electric flux solved examples

In the following, a number of solved examples of electric flux are presented. More simple problems including flux of uniform or non-uniform electric fields are also provided.

Example (1): electric flux through a cylinder.

Suppose in a uniform electric field a cylinder is placed such that its axis is parallel to the field.

To compute the flux passing through the cylinder we must divide it into three parts top, bottom, and curve then the contribution of these parts to the total flux must be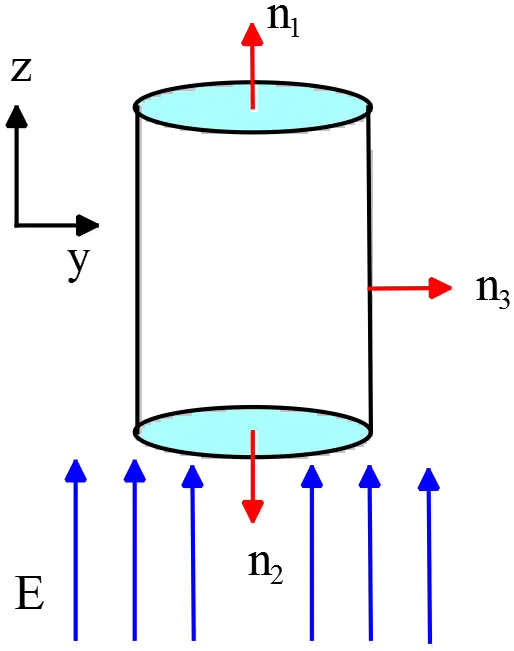electric flux through cylinder summed.

On the top and bottom sides, the unit normal vectors are $\hat k$, $-\hat k$, respectively. Let $\vec E$ be toward the $z$ axis i.e. $\vec E=E\hat k$.

Scalar products of top and bottom sides by electric field make the total flux since the normal vectors and $\vec E$ are parallel ($\theta =0$) and antiparallel ($\theta=180^\circ$), respectively.

The curve side has a normal vector in the radial direction which makes a right angle($θ=90^\circ$) with $\vec E$ so its contribution to the flux is zero. \begin{align*} \oint{\vec E\cdot \hat n dA}&=\int{\vec E_1\cdot\hat k dA_1}+\int{\vec E_2 \cdot \left(-\hat k\right) dA_2}\\ &+\int{\vec E_3 \cdot \hat r dA_3}\\&=E_1 A_1 -E_2A_2\end{align*}

$E_1$, $E_2$ and $E_3$ are the amount of electric fields passing through the surfaces. Since the electric field is uniform one can factor it out of the integral.

$A_3$ is the area of the curved side which is $2\pi Rl$. The electric field lines don’t pass through the curved sides and only penetrate top and bottom which in this case their amounts are the same $E_1=E_2$.

Therefore, the total flux through the cylinder is simply \[\Phi_E=0\]
This result is expected since the whole electric field entering the bottom side exiting the top surface.

Example (2):

A hemisphere of radius $R$ is placed in a uniform electric field such that its central axis electric flux through hemisphereis parallel to the field. Find the electric flux through it?

 

Solution:

Let the electric field be in the $z$ direction i.e. $\vec E=E_0 \hat k$. The normal vector to the hemisphere is in the radial direction so $\hat n=\hat r$. Further, the area element of a spherical surface of a constant radius in the spherical coordinate is 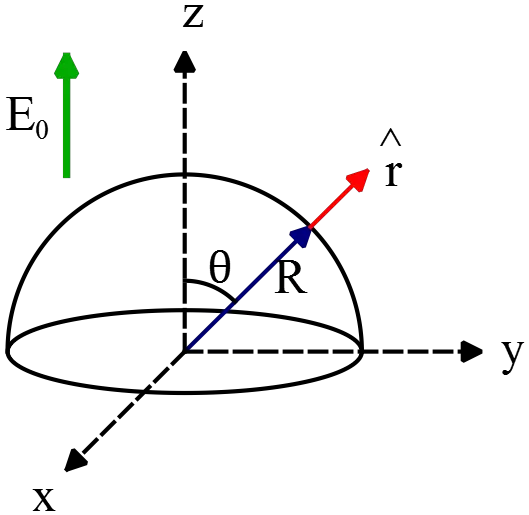unit vectors on sphere$dA=R^{2}\,\sin\theta\, d\theta d\phi$.

Therefore,
\begin{align*}\Phi_E&=\int{\vec E\cdot \hat n\,dA}\\&=\int{\left(E_0\hat k\right)\cdot \hat r R^{2}\,\sin \theta d\theta d\phi}\end{align*}
No we must find the scalar product of $\hat r\cdot \hat k$. In spherical coordinates we have the following relation for the unit vector in the radial direction:
\[\hat r=\sin \theta \cos \phi \, \hat i+\sin \theta \sin \phi \, \hat j+\cos \theta \, \hat k\]
Where $\hat i,\hat j,\hat k$ are the usual unit vectors in the Cartesian coordinates. Thus
\[\hat r\cdot \hat k=\cos \theta\]
Where we have used the fact that $\hat i\cdot \hat k=\hat j\cdot \hat k=0$ and $\hat k\cdot \hat k=1$. Putting everything into the electric flux relation, one can obtain
\begin{align*}\Phi_E&=E_0R^{2}\int_0^2\pi{d\phi}\int_0^{\pi/2}{\underbrace{\cos \theta \sin \theta}_{\frac 12 \sin 2\theta}d\theta}\\&=E_0R^{2}\left(2\pi\right)\frac 12\left(-\frac 12\,\cos 2\theta\right)_0^{\pi/2}\\&=\pi E_0R^{2}\end{align*}

Example (3):

consider a planar disc of radius $12\,{\mathrm cm}$ that makes some angle $30^\circ$ with the uniform electric field $\vec E=450\,\hat i\,\mathrm {(N/C)}$. What is the amount of electric flux passing through it?

Solution:

Let the electric field be in the x-direction and normal to the plane be in some direction $\hat n$ which must be decomposed into the $x$ and $y$ directions, as shown in the 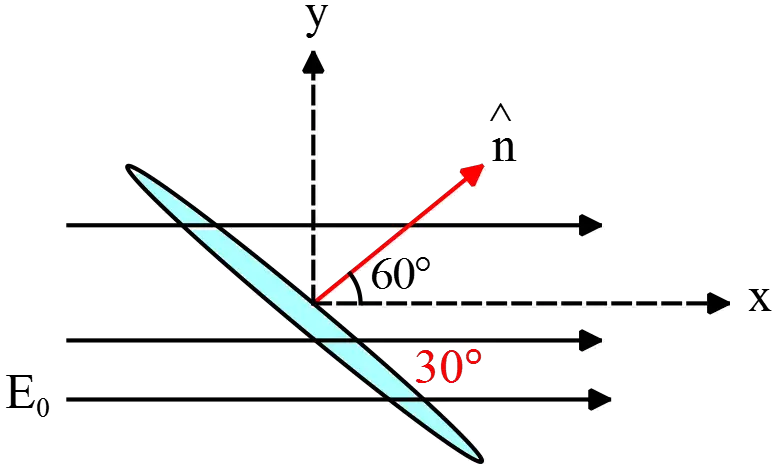electric flux through planar disk examplefigure. Using the definition of electric flux, we have
\begin{align*} \Phi_E&=\int{\vec E\cdot \hat n dA}\\&=\int{E_0\hat i \cdot\left(\cos 60^\circ\,\hat i+\sin 60^\circ \,\hat j\right)dA}\\&=E_0\,\cos 60^\circ\int{dA}\end{align*}
Where the integral over $dA$ is the area of the disk which is $\pi R^{2}$. Therefore
\begin{align*}\Phi_E&=E_0\left(\frac 12\right)\left(\pi R^{2}\right)\\&=(450)\left(\frac 12 \right)\pi (0.12)^{2}\\&=10.17 \quad \rm {\frac {N\cdot m^{2}}{C}}\end{align*}

Another method for finding electric flux due to systems with high symmetry is to use Gauss's law.  You can also learn this elegant method with some simple problems.

 

 

© 2015 All rights reserved. by