AP Physics 1: Kinematics Practice Problems with Answers
This comprehensive collection features a complete set of multiple-choice questions on kinematics from the AP Physics 1 exam. Each section of kinematics is represented, with fully worked solutions provided for every question. This is an invaluable resource for anyone seeking to master the complexities of kinematics.
If you’re preparing for the AP Physics 1 exam in 2025, be sure to download our ultimate equation sheet. It’s the perfect study aid for those late-night revision sessions. Start your journey towards AP Physics 1 success today!
AP Physics Kinematics Practice Problems
Problem (1): The position vs. time graph for a moving object along the $x$ axis is shown in the figure below.
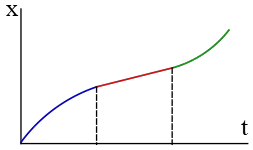
Which of the following graphs is the corresponding velocity vs. time graph?
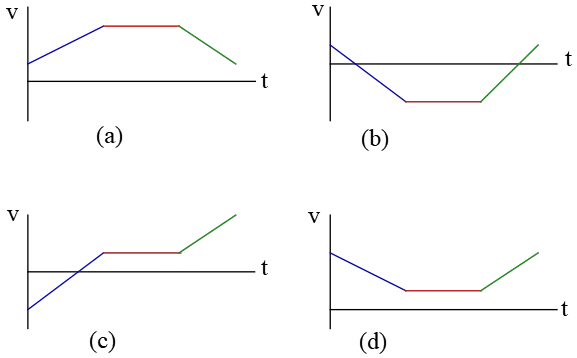
Solution: This problem is similar to many found in AP Physics kinematics practice problems, so let’s examine it in detail.
The motion consists of three parts: two curves and one straight line.
The slope of a tangent line at each point on an $x-t$ curve represents the velocity of the object. Slopes with an acute angle ($\alpha<90^\circ$) indicate a positive velocity, while slopes with an obtuse angle ($\alpha>90^\circ$) indicate a negative velocity. Note that these angles are measured relative to the positive $x$-axis.
In the first part (the blue curve), the slope at the starting point, which represents the initial velocity $v_0$, has an acute angle, indicating that $v_0>0$. Throughout this time interval, all slopes have acute angles and are decreasing, suggesting that velocities are positive and decreasing in magnitude.
The middle part (the red straight line) has a constant slope throughout its time interval, indicating that the velocity is constant during this time interval. The object continues to move at the same velocity as it did in the last second of the previous part.
The final part (the red curve) also has positive slopes, but the angles increase, implying that velocities are increasing in magnitude and positive.
Based on these explanations, we can conclude that option (d) is correct. Hence, the correct answer is (d).
Problem (2): The velocity-versus-time graph of a moving object is shown in the figure below. Over time, which of the following is correct?
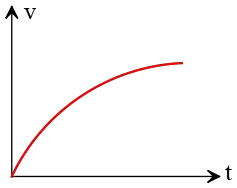
(a) the velocity and acceleration are increasing.
(b) the velocity and acceleration are decreasing.
(c) the velocity increases but the acceleration decreases.
(d) the velocity decreases but the acceleration increases.
Solution: It is obvious that the object's velocity is increasing over time. The slope of a tangent line on a velocity vs. time graph always represents the magnitude and direction of acceleration. In this case, it can be observed that the slopes decrease from the initial time until they reach the final point on the graph. Therefore, we can conclude that the object's acceleration is decreasing. Hence, the correct answer is (c).
Problem (3): Which of the following graphs shows the position vs. time graph for an object thrown vertically upward into the air?
Solution: The fundamental kinematic equation for an object moving with constant acceleration along a straight line is $x=\frac 12 at^2+v_0 t+x_0$ for horizontal motion, or $y=-\frac 12 gt^2+v_0t+y_0$ for vertical motion. In this problem, the object is thrown vertically upward, so its position at each moment is given by the second equation. Due to the $-\frac 12 g$ term in the second equation, the parabola is concave downward.
Among the given graphs, only graph (b) has the shape of a downward-concave parabola.
Hence, the correct answer is (b).
Problem (4): The position vs. time graph of a moving object is shown in the figure below. How many times has the direction of the object changed?
(a) 1 (b) 2 (c) 3 (d) None.
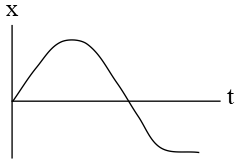
Solution: When given a position vs. time graph and asked to determine the moments when the object changes its direction, use the following method: Identify where the tangent line on the graph is horizontal. Remember that the slope of the tangent line on the $x-t$ graph always represents the direction and magnitude of the velocity at any instant of time.
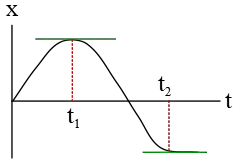
So, where these tangent lines become zero (horizontal), the object reverses its direction. In the given graph, at times $t_1$ and $t_2$, the tangents are horizontal, indicating that at these two points (positions), the direction of motion is reversed. However, note that after time $t_2$, the position of the object does not change, which means the object has stopped. Thus, overall, the object has changed its direction only once. Hence, the correct answer is (a).
Problem (5): Consider the position vs. time graph for a moving object, as shown in the figure below. At which numbered points does the object have the greatest speed?
(a) 1 (b) 2 (c) 3 (d) 4
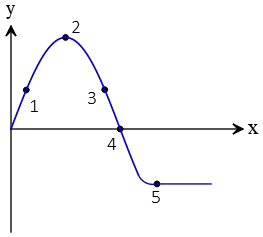
Solution: The slope of a tangent line at each point on an $x-t$ graph represents the magnitude (speed) and direction of the velocity vector at that point. If we start drawing slopes at the origin or point $4$, we notice that as we get closer to the top of the graph, the slopes become smaller and smaller. This continuous decrease in the slope of the curves indicates that the velocities are also decreasing until they reach the top of the curve, where the velocity becomes zero. Based on this reasoning, we conclude that the slope at the numbered point $4$ must be the greatest.
Hence, the correct answer is (d).
Problem (7): The position vs. time graph for a moving object is shown in the figure below. How many times has the speed been zeroed and how many times has it reversed its direction, respectively?
(a) 1,1 (b) 2,2 (3) 1,2 (4) 2,1
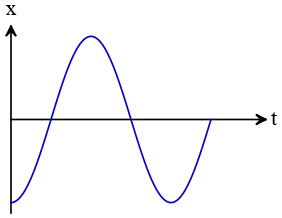
Solution: The speed of an object is zero where the tangent to the $x-t$ curve becomes horizontal. As you can see, there are three points where the tangents are horizontal. Therefore, in these instants, the speed of the object is zero.
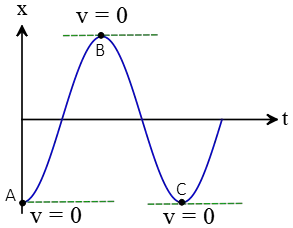
Remember that when the speed of a moving object becomes zero, it either changes direction or stops. Thus, at the three points shown above, the object changes its direction.
Hence, the correct answer is (b).
Problem (8): According to the figure below a car is moving at a constant rate along the $x$ axis.
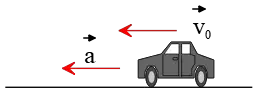
Which of the following velocity vs. time graphs describes the motion of the car?
Solution: Take the positive to the right. The car is moving to the left, so the direction of its velocity is negative. Therefore, the first choice is incorrect since all the car’s velocities are positive, indicating movement to the right. The car begins to move non-stop to the left (in the negative direction), so its velocity is negative at all times. Thus, choices (2) and (3) are also incorrect.
Note that the phrase ''at a constant rate'' implies constant acceleration.
On the other hand, the acceleration is also directed to the left. We know that the slope of the velocity-time graph provides the direction and magnitude of the acceleration. If the angle that the slope makes with the horizontal is obtuse ($\alpha >90^\circ$), then the direction of the acceleration is negative.
Hence, the correct answer is (d).
Problem (9): A car moving along the $x$ axis with a constant acceleration. If its velocity-versus-time graph is as below,
Which of the following describes the motion of the car?
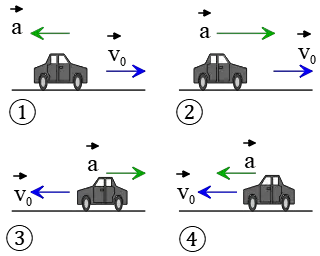
Solution: First of all, choose a positive direction, say to the right. The graph shows us the initial velocity is positive. So, the car starts to move to the right initially. Thus, choices (3) and (4) are wrong. Since the graph does not intersect the time axis, it means that the velocity does not get zero, so the car continues to move to the right non-stop.
Now we must say something about the car's acceleration. Recall that the slope of a velocity-time graph gives the magnitude and direction of the acceleration. In this case, the slope makes an obtuse angle ($\alpha >90^\circ$) with the horizontal, which means the acceleration is negative or is toward the left. So, choice (2) is also incorrect.
Hence, the correct answer is (1).
Problem (10): The position of a moving object at any instant is given by equation $x=4t^2-6t+3$. What is the average velocity of the object between $t=1\,{\rm s}$ and $t=4\,{\rm s}$?
(a) 14 (b) 15 (c) 16 (d) 18
Solution: The average velocity in physics is defined as the ratio of displacement to the time interval. It is given by \[v_{av}=\frac{x_2-x_1}{t_2-t_1}\] The positions at $4\,{\rm s}$ and $1\,{\rm s}$ can be calculated as follows: \begin{align*} x_1&=4(1)^2-6(1)+3 \\&=1\,{\rm m} \\\\\ x_4&=4(4)^2-6(4)+3 \\&=43\,{\rm m}\end{align*} Using the definition of average velocity, we find \[v_{av}=\frac{43-1}{4-1}=14\,{\rm m/s}\]
Hence, the correct answer is (a).
Method two: The position equation reveals that the motion has constant acceleration since it has the form of a quadratic equation. Comparing this with the standard position kinematic equation $x=\frac 12 at^2+v_0t+x_0$, we can find the acceleration $a$, the initial velocity $v_0$, and the initial position $x_0$ of the object as follows: \begin{gather*} \frac 12 a=4 \Rightarrow \quad a=8\,{\rm m/s^2} \\\\ v_0=-6\,{\rm m/s}\\\\ x_0=3\,{\rm m}\end{gather*} Substituting these kinematics variables into the velocity kinematics equation $v=v_0+at$, we can find the object's velocity at any instant of time \[v=-6+8t\] Knowing the velocity versus time equation, we can determine the average velocity using the following formula \[v_{av}=\frac{v_1+v_2}{2}\] The rest is left as a practice problem for you.
Problem (11): A stone is thrown vertically upward into the air with an initial speed of $10\,{\rm m/s}$. After how many seconds does its velocity become $5\,{\rm m/s}$ downward?
(a) 0.5 (b) 1.5 (c) 2.5 (d) 2
Solution: Let’s take upward as the positive direction, so the initial velocity is positive $v_0=+10\,{\rm m/s}$. The velocity kinematic equation $v=v_0-gt$ gives us the velocity at any moment. We are asked to find the time when the velocity is $5\,{\rm m/s}$ downward, which means $v=-5\,{\rm m/s}$ (Note the negative sign). Substituting this information into the above velocity equation and solving for time, we get $t$: \begin{gather*} v=v_0-gt \\\\ -5=10-(10)t \\\\ \Rightarrow \quad t=1.5\,{\rm s}\end{gather*} Hence, the correct answer is (b).
Problem (12): A car is moving at a constant speed of $54\,{\rm km/h}$ along a straight path. It applies brakes and stops after traveling a distance of $22.5\,{\rm m}$. How long is the stopping time?
(a) 6 (b) 5 (c) 2 (d) 3
Solution: In such AP kinematics questions, we need to analyze only the braking stage. When the brakes are applied, the previous constant velocity becomes the initial velocity. From this moment, the velocity will change with time until it comes to a stop. So, during this stage, we have $v_0=54\,{\rm km/h}$, $v=0$, and $\Delta x=22.5\,{\rm m}$. Substituting these into the time-independent kinematic equation $v^2-v_0^2=2a\Delta x$ and solving for $a$ yields: \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ 0-15^2=2a(22.5) \\\\ \Rightarrow \quad a=-5\,{\rm m/s^2}\end{gather*} In the above, we converted the velocity units to the SI units ${\rm m/s}$ as follows: \[54\,\frac{km}{h}=54\left(\frac{1000}{3600}\right)\frac ms=15\,\frac ms\] Now, we use the velocity kinematic equation $v=v_0+at$ and solve for $t$: \begin{gather*} v=v_0+at \\\\ 0=15+(-5)t \\\\ \Rightarrow \quad t=3\,{\rm s}\end{gather*} Hence, the correct answer is (d).
Quicker method: In all constant acceleration kinematics problems, we can use the following important formula: \[\Delta x=\frac{v_1+v_2}{2}\Delta t\] where $v_1$ and $v_2$ are the initial and final velocities during the accelerating stage, respectively. Here, $v_1=15\,{\rm m/s}$, $v_2=0$, and $\Delta x=22.5\,{\rm m}$. Substituting these into the above formula and solving for $t$ gives the same previous result.
Problem (13): The velocity of a car changes from $5\,{\rm m/s}$ to $7\,{\rm m/s}$ at a constant rate in a time interval of $5\,{\rm s}$. How long does the car move during this time period?
(a) 120 m (b) 30 m
(c) 15 m (d) 45 m
Solution: There are two methods to arrive at the answer. The longer way is to first find the car's acceleration, then use the equation $v=v_0+at$ and solve for $t$. A much shorter way, which is suitable for the AP Physics exam, is to use the following formula: \[\Delta x=\frac{v_1+v_2}{2}\Delta t\] Substituting the known numerical values into this formula and solving for $t$, we find \begin{align*} \Delta x&=\frac{v_1+v_2}{2}\Delta t\\\\ &=\frac{5+7}{2}(5) \\\\&=\boxed{30\quad {\rm m}}\end{align*} Hence, the correct answer is (b).
Problem (14): From the top of a height of 25 m, a bullet is thrown vertically into the air with an initial velocity of $20\,{\rm m/s}$. After how many seconds does the direction of motion of the bullet change?
(a) 2 (b) 3 (c) 4 (d) 5
Solution: Let’s take the throwing point as the origin, so $y_0=0$. The bullet rises until it reaches a point where its speed becomes zero. At this moment, it reverses its direction and starts to descend. During the ascent, the velocities at the initial and final points are known. Therefore, we can solve the kinematic equation $v=v_0-gt$ for $t$. \begin{gather*} v=v_0-gt \\\\ 0=20-10t \\\\ \Rightarrow \quad \boxed{t=2\,{\rm s}}\end{gather*} Hence, the correct answer is (a).
Problem (15): In a projectile motion in a two-dimensional plane vertically, which of the following is correct:
(a) the vertical component of velocity is constant.
(b) the projectile's velocity is constant.
(c) the range of the projectile is independent of the throwing angle.
(d) the horizontal component of velocity remains constant.
Solution: The best approach to answering these kinds of kinematics questions in the AP physics exam is to utilize the projectile motion formulas.
(a) the vertical component of a projectile's velocity is given by $v_y=v_0\sin\theta-gt$. As you can see, this component varies with time. Therefore, this choice is incorrect.
(b) The speed of the projectile definitely changes. Initially, it is launched with a certain speed, and at a later time, at the highest point, its velocity becomes zero. So, this choice is also incorrect.
(c) The range of a projectile is determined by $x=(v_0\cos\theta)t$. The range also changes with time.
(d) The horizontal component of the projectile's velocity is computed by $v_x=v_0\cos\theta$. As you can see, this component is independent of time, so it remains constant during the motion.
Hence, the correct answer is (d).
Review all the AP Physics formulas in one place to memorize them for the night exam.
Problem (16): A particle moves around a circle at a constant speed $v$. How many times is the change in velocity at points $A$ and $B$ relative to the magnitude of the velocity?
(a) zero (b) 1 (c) $\frac 12$ (d) $\frac{\sqrt{3}}2$
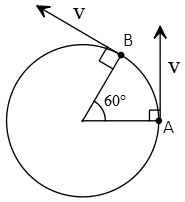
Solution: The change in velocities at points $A$ and $B$ is also a vector quantity, $\Delta \vec{v}=\vec{v}_B-\vec{v}_A$. The problem has asked us to find the magnitude of this vector and compare it with the constant speed $v$ around the circle.
This change in velocity vector is a subtraction vector whose magnitude is given by the following formula \[\Delta v=\sqrt{v_A^2+v_B^2-2v_A v_B \cos\theta}\] where $\theta$ is the angle between the two vectors. To find this angle, we must bring the velocity vectors to a point as shown below.
Thus, the desired angle is $\theta=60^\circ$. Substituting $v_A=v_B=v$ into the above equation gives \begin{align*} \Delta v &=\sqrt{v_A^2+v_B^2-2v_A v_B \cos\theta} \\\\ &=\sqrt{v^2+v^2-2v^2\cos 60^\circ}\\\\ &=v\end{align*} The ratio wanted is found below \[\frac{\Delta v}{v}=\frac{v}{v}=1\] Hence, the correct answer is (b).
More related articles:
Definition of a vector in physics
Practice problems on vectors and unit vectors.
Problem (17): A moving object revolves $90^\circ$ around a circle of radius $R$. How many times is the distance traveled by the object relative to the displacement?
(a) $\pi R/2$ (b) $R\sqrt{2}$
(c) $\pi/2$ (d) $\pi \sqrt{2}/4$
Solution: This refers to the vector problem in the AP physics exam. The distance traveled is simply one-fourth of the circumference of the circle. Thus, \begin{align*} D&=\frac 14 (circumference) \\\\ &=\frac 14 (2\pi R) \\\\ &=\frac{\pi R}{2}\end{align*} The object initially is at point $A$ and finally at point $B$.
From the origin, draw vectors that end at the locations of points $A$ and $B$. These vectors are called position vectors.
The displacement vector is a vector that connects the initial point to the final point as shown (red dotted line) or \[\vec{d}=\vec{R}_2-\vec{R}_1\] Thus, we must find the magnitude of this subtraction vector with the following standard formula \begin{align*} d&=\sqrt{R_1^2+R_2^2-2R_1 R_2 \cos\theta} \\\\ &=\sqrt{R^2+R^2-2R^2 \cos 90^\circ}\\\\ &=\sqrt{2R^2}\\\\&=R\sqrt{2}\end{align*} where in the above, $R$ and $\theta$ are the magnitudes of the position vectors and angle between them, respectively. Now construct their ratio as below: \[\frac{D}{d}=\frac{\frac{\pi R}{2}}{R\sqrt{2}}=\frac{\pi \sqrt{2}}{4}\] Hence, the correct answer is (d).
Problem (18): An object is kicked horizontally with an initial velocity of $25\,{\rm m/s}$ and travels a horizontal distance of $50\,{\rm m}$ before landing. From what height was this ball thrown? (Ignore air resistance.)
(a) 20 m (b) 30 m
(c) 25 m (d) 45 m
Solution: This is another type of projectile motion problem that appears in all the AP Physics exams. First, list all the given data: horizontally kicked or thrown means the angle of the projectile is zero, $\theta=0$. The initial speed is $v_0=25\,{\rm m/s}$, and the horizontal distance traveled (which is the same range of projectile) is $50\,{\rm m}$.
To begin, calculate the total time the object is in the air using the projectile horizontal displacement formula $\Delta x=(v_0\cos\theta)t$. \begin{gather*} \Delta x=(v_0 \cos\theta)t \\\\ 50=(25\cos 0)t \\\\ \Rightarrow \quad t=2\,{\rm s}\end{gather*} where we used $\cos 0=1$. Now, use the projectile vertical displacement formula $y=-\frac 12 gt^2+(v_0\sin\theta)t+y_0$ and substitute the time $t$ found above into it and solve for $y$. But there is an important note about using this formula in all projectile motion problems and that is choosing a suitable coordinate system.
If we choose the initial throwing point as the origin, in this case, the initial position $y_0$ is set to zero, $y_0=0$ and this simplifies our calculations. Thus, \begin{align*} y&=-\frac 12 gt^2+(v_0\sin\theta)t+y_0 \\\\ &=-\frac 12 (10)(2)^2+0+0 \\\\ &=-20\,{\rm m}\end{align*} since $\sin 0=0$, we ignored that second term in the above and set it to zero. The negative indicates that the object will land $\boxed{20\,{\rm m}}$ below our hypothetical origin.
Hence, the correct answer is (a).
Problem (19): A $20\,{\rm g}$ ball is thrown with an initial velocity of $20\,{\rm m/s}$ vertically upward. How high does the ball reach after 2 seconds?
(a) 10 m (b) 30 m
(c) 20 m (d) 40 m
Solution: The object travels vertically, so it is better to use the freely falling kinematics equations. In this case, the vertical displacement is found using \[\Delta y=-\frac 12 gt^2+v_0t\] If we choose the starting point as the origin, then $\Delta y$ gives us the vertical distance traveled by the object. Substituting the known numerical values into it, we will have \begin{align*} \Delta y&=-\frac 12 gt^2+v_0t\\\\ &=-\frac 12 (10) (2)^2+(20)(2) \\\\ &=\boxed{+20\,{\rm m}}\end{align*} Hence, the correct answer is (c).
Problem (20): From a height of $30\,{\rm m}$, a stone is thrown vertically downward with an initial speed of $5\,{\rm m/s}$. How many seconds after throwing the stone strike the ground?
(a) 1s (b) 2s
(c) 3s (d) 4s
Solution: Choose the starting point to be the origin, so the initial position becomes zero in the kinematics equations, $y_0=0$. The stone strikes 30 m below our origin, so its coordinate is $y=-30\,{\rm m}$. Note that the object moves down initially, so its velocity must be accompanied by a minus sign: $v_0=-5\,{\rm m/}$. The unknown is time $t$. Substitute this information into the vertical displacement kinematics equation below and solve for $t$ \begin{gather*} y=-\frac 12 gt^2+v_0t+y_0 \\\\ -30=-\frac 12 (10)t^2+(-5)t+0 \\\\ 5t^2+5t-30=0\end{gather*} This is a quadratic equation of the form $at^2+bt+c$ whose solutions is found as below \[t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\] By putting the coefficients in the above equation, we have \begin{gather*} t=\frac{-5\pm\sqrt{5^2-4(5)(-30)}}{2(5)} \\\\ \boxed{t_1=2\,{\rm s}}\\\\ t_2=-3 \end{gather*} It is obvious that time cannot be negative. Hence, the correct answer is (b).
Problem (21): The position vs. time graph of a moving object is shown in the figure below. Is the object speeding up or slowing down at points $A$ and $B$, respectively?
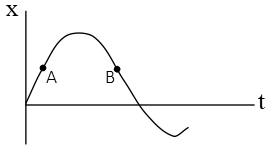
(a) Slowing down - speeding up.
(b) Both are slowing down.
(c) Both are speeding up.
(d) Speeding up - slowing down.
Solution: The terms ''speeding up'' or ''slowing down'' refer to an increase or decrease in the speed of a moving object, respectively. To determine this property at each point of an $x-t$ graph, we must determine the product $av$ at that particular point. If $av>0$ then the motion is speeding up, and if $av<0$ the motion is slowing down.
On the other hand, we know that the slope of a tangent line at each point on an $x-t$ curve gives the magnitude and direction of velocity at that point. If the slope makes an acute angle ($\alpha<90^\circ$) with the $+x$ direction, then $v<0$.
Opening up or down the curve (which is called concavity) also shows the sign (or direction) of the acceleration. For opening up concavity $a>0$ and for concavity down $a<0$.
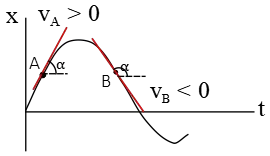
In this case, the points $A$ and $B$ lie on a curve that is opened downward so at both points we have $a>0$. The tangent line slope at point $A$ is an acute angle, so $v_A>0$ and it makes an obtuse angle at point $B$, so $v_B>0$.
Therefore, for point $A$ we have $a_A v_A>0$, so the object is speeding up. Similarly, at point $B$, $a_B v_B<0$, the object is slowing down.
Hence, the correct answer is (d).
Problem (22): A ball is thrown vertically upward into the air. What is the magnitude of the ball's acceleration just after leaving your hand?
(a) greater than g (b) less than g
(c) equal g (d) zero.
Solution: Any motion in which the object is moving freely under the influence of gravity alone is called a freely falling motion. This definition is independent of the conditions of the initial motion. Objects thrown straight up or down and/or released from rest are all considered freely falling objects.
In this case, the only acceleration that the object experiences is the gravitational acceleration $g=9.8\,{\rm m/s^2}$. With these explanations, the correct answer is (c).
Author: Dr. Ali Nemati
Date Published: November 11, 2021
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.