In this article, we have attempted to teach you the formulas for projectile motion by presenting some solved examples. Through this method, you will gain a better understanding of the equations for projectiles.
Definition of projectile motion:
Projectile motion refers to the motion of any object that is thrown into the air at an angle $\theta$. It is characterized by motion in two dimensions and is solely influenced by gravitational force.
Projectile Motion Formulas:
The following equations represent projectile motion in the vertical and horizontal directions.
In the horizontal direction:
\begin{align*} \text{Displacement}&:\,\Delta x=\underbrace{\left(v_0 \cos \theta\right)}_{v_{0x}}t\\ \text{Velocity}&:\, v_x=v_0 \cos \theta \end{align*}
In the vertical direction:
\begin{align*} \text{Displacement}&:\, \Delta y=\frac 12 (-g)t^2 +(\underbrace{v_0 \sin \theta}_{v_{0y}})\,t\\ \text{Velocity I}&:\, v_y = \underbrace{v_0 \sin \theta}_{v_{0y}}+(-g)t \\ \text{Velocity II}&:\, v_y^2 -\left(v_0 \sin \theta\right)^2=2(-g)\Delta y \end{align*}
The formula for the speed of an object in projectile motion (Using the Pythagorean theorem):
\[ v=\sqrt{v_x^2 + v_y^2 }\]
The formula for the angle of the velocity vector at any time with respect to the +x-axis:
\begin{align*} \theta &= \tan^{-1} \left(\frac{v_y}{v_x}\right)\\ &=\tan^{-1} \left(\frac{v_0 \sin \theta -gt}{v_0 \cos \theta}\right) \end{align*}
The formula for the path of the projectile (Trajectory path equation):
\[ y(x)=x\:\tan \theta-\frac{gx^2}{2v_0^2\,\cos^2 \theta}\] Here, $y$ and $x$ represent the vertical and horizontal displacements, respectively. $\theta$ denotes the angle with respect to the horizontal, and $v_0$ represents the initial speed.
Horizontal Range of a Projectile:
The horizontal distance between the launch and striking points is known as the Range of Projectile, and its equation is given by \[ R= \frac{v_0^2}{g}\,\sin 2\theta\]
Total Time of Flight for a Projectile:
The total time of flight for a projectile in the air can be calculated using the formula \[ t=\frac{2v_0 \sin \theta}{g}\]
The formula for the maximum height reached by a projectile:
\[ H=\frac{v_0^2 \sin^2 \theta}{2g}\]
Horizontal Projectile Motion Formula:
The formula for horizontal projectile motion is as follows: All of the above formulas are based on a non-zero launch angle.
However, if the projectile is thrown in the air at an angle of $\theta=0$, then there is no $y$-component of the initial velocity, meaning $v_{0y}=0$.
This scenario is known as horizontal projectile motion, and its formulas are as follows: \begin{gather*} v_{0x}=v_0 \quad , v_{0y}=0 \\\\ \Delta x=v_0 \,t \quad , \Delta y=-\frac 12 gt^2 \\\\ v_x=v_{0x} \quad , v_y=-gt \\\\ v^{2}=-2g\Delta y \end{gather*} Please refer to Example (3) below for further clarification.
To practice using these formulas for projectile motion, please refer to the following solved examples. For more problems, you can also refer to projectile motion problems.
Projectile Motion Solved Examples:
Example (1):
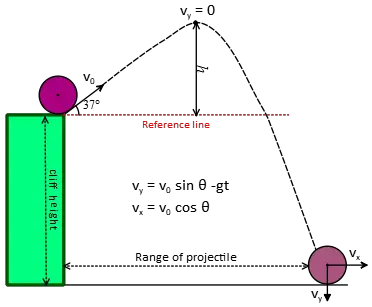
A projectile is fired from a cliff with a height of $200\,{\rm m}$ at an angle of $37^\circ$ from the horizontal with an initial velocity of $150\,{\rm m/s}$. Find the following:
(a) The distance at which the projectile hit the ground.
(b) The maximum height above the ground reached by the projectile.
(c) The magnitude and direction of the projectile velocity vector at the instant of impact to the ground.
Solution:
Let's consider the firing point as the origin of our coordinate system. We will take upward as positive for $y$ and rightward as positive for $x$. Since the projectile hits the ground below our chosen origin, its coordinates are $(x=?,y=-200\,{\rm m})$.
(a) The formula for the horizontal distance of a projectile is given by $\Delta x=(v_0\,\cos \theta)\, t$. We are asked to find the total distance from the launching point to the striking point $(x=?,y=-200\,{\rm m})$, which is known as the range of the projectile. Therefore, we need to determine the total time of flight.
To find the total time of flight, we can use the equation $y=-\frac 12 g\,t^2 + (v_0 \sin \theta)\,t +y_0$. Substituting $y=-200$, $g=9.8$, $v_0=150$, $\theta=37^\circ$, and $y_0=0$ into this equation, we get: \begin{align*} y&=-\frac 12 g\,t^2 + (v_0 \sin \theta)\,t +y_0 \\ -200&=-\frac 12 (9.8)\,t^2 + (150\times\,\sin 37^\circ)\,t+0\\ &\Longrightarrow \ 4.8\,t^2-90\,t-200=0 \end{align*} The solution to this quadratic equation $ax^2 + bx+c=0$ is given by: \[x=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}\] Using this formula, we can find the total time of flight as follows: \begin{align*}t&=\frac{90\pm\sqrt{(90)^2-4\,(4.8)(-200)}}{2(4.8)}\\ &= t_1=20.757\,{\rm s} \\ &\text{and} \\ t_2&\approx-2\,{\rm s} \end{align*} Since the projectile is fired at $t=0$, the time of strike can not be a negative value. Thus, the total time is $t=20.757\,{\rm s}$.
Now, we can substitute this value into the horizontal distance formula to find the range of the projectile \begin{align*} \Delta x&=(v_0\,\cos \theta)\, t \\ &=(150\times \,\cos 37^\circ)(20.757) \\ &=(150\times 0.8)(20.757) \\ &=95.83\,{\rm m} \end{align*}
(b) One of the key features of projectile motions is that its vertical velocity, $v_y$, at the highest point of trajectory is zero. By setting $v_y=0$, we can find the time between the initial time and when the projectile reaches the highest point.
Thus, using the equation for projectile vertical velocity at any time, $v_y = v_0\sin \theta - gt$, and setting $v_y$ to zero, we have: \begin{align*} v_y&=v_0\,\sin \theta-gt\\ 0&=150\times \sin 37^\circ-(9.8)\,t \end{align*} Solving this linear equation for $t$, we find the time between firing and the highest point as $t=9.2\,{\rm s}$. Substituting this time into the projectile formula for vertical displacement, we have: \begin{align*} y&=-\frac 12 gt^2 + (v_0\,\sin \theta)\,t+y_0 \\ h&=-\frac 12 (9.8)(9.2)^2 + (150\times \sin 37^\circ)(9.2)+0\\ h&=415.76\,{\rm m} \end{align*} Since we adopted the origin of the coordinate $(x_0=0,y_0=0)$ at the firing point, we set $y_0$ to zero in the second line. Adding this value with the cliff height, the total height the projectile reaches from the ground is: \[H=d+h=200+415.76=615.76\,{\rm m}\]
(c) To find the velocity of a projectile at any time, we need to compute its components at any instant of time. First, calculate the vertical and horizontal components of velocity and then use the Pythagorean theorem to find the resultant velocity vector.
The vertical speed is given by $v_y = (v_0 \sin \theta) - gt$. Substituting the given values, we have: \begin{align*} v_y&=(v_0 \sin \theta)-gt\\ &=(150\times \sin 37^\circ)-(9.8\times 20.757)\\ v_y&=-113.14\,{\rm m/s} \end{align*} The negative sign indicates that the projectile is moving downward.
The horizontal speed is given by $v_x = v_0\cos \theta$. Substituting the given values, we have: \begin{align*} v_x&=v_0\,\cos \theta \\ &=150\times \cos 37^\circ \\ v_x&=119.79\,{\rm m/s} \end{align*} Note that in above we put the total time in the vertical speed formula. Given those components, it is an easy task to find the magnitude and direction of the velocity vector \begin{align*} v&=\sqrt{v_x^2 + v_y^2}\\ &=\sqrt{(119.79)^2 + (-113.14)^2}\\ &=164.77\,{\rm m/s}\\ \text{AND}\\ \theta &= \tan^{-1} \left(\frac{v_y}{v_x}\right)\\ &=\tan^{-1} \left(\frac{-113.14}{119.79}\right)\\ &=-43.36^\circ \end{align*} The negative indicates the angle is below the horizontal axis.
Example (2):
A bird carrying a juniper berry suddenly releases the berry when it is $30\,{\rm m}$ above the level ground. At the instant the berry is released it has a velocity of $10\,{\rm m/s}$ at an angle of $20^\circ$ from horizontal. Find:
(a) The time the berry reaches the ground.
(b) The velocity vector of the berry when it reaches the ground.
Solution:
This is a projectile motion problem since the berry has an angle and velocity and under the effect of gravity reaches the ground.
(a) Let the releasing point be the origin of the coordinate i.e. $(x_0=0,y_0=0)$. Since the berry hit the ground below the y-axis so the coordinate of impact is $(x=?,y=-h=-30)$, where $h$ is the vertical distance from the bird to the hitting point. \[\begin{aligned} y&=-\frac 12 gt^2 + (v_0\,\sin \theta)\,t+y_0\\ -30&=-\frac 12 (9.8)\,t^2 + (10\times \sin 20^\circ)\,t+0\\ & \Rightarrow \,t_1=2.848\,{\rm s} \ , \ t_2=-2.15\,{\rm s} \end{aligned}\] Since the berry dropped at the initial time $t=0$, so the total time the berry is in the air (accepted time) is $t_1=2.848\,{\rm s}$.
(b) The components of the velocity vector are determined as \begin{align*}\text{Vertical component}: \, v_y&=(v_0 \sin \theta)-gt\\ &=(10\times \sin 20^\circ)-(9.8\times 2.848)\\ v_y&=-24.5\,{\rm m/s}\\ \text{Horizontal component}:\, v_x &=v_0\,\cos \theta \\ &=10\times \cos 20^\circ \\ v_x &=9.4\,{\rm m/s} \end{align*} Thus, the vector addition of those components gets the velocity vector \begin{align*} \vec{v}&=v_x\,\hat{i} + v_y\,\hat{j}\\ &=9.4\,\hat{i} -24.5\,\hat{j} \end{align*}
Example (3) for the horizontal projectile motion:
A stone is thrown horizontally into the air with a speed of $8\,{\rm m/s}$ from the top of a $20\,{\rm m}$-high cliff and hits the ground.
(a) At what distance from the base of the cliff does the stone land?
(b) Find the speed and direction of the stone just before it hits the ground.
Solution: Since it is said that the stone is thrown horizontally, we can conclude that $\theta=0$. Let the origin of the coordinate system be the throwing point, which is $(x_0=0,y_0=0)$, and let the coordinates of the landing point be $(x=?,y=-20\,{\rm m})$.
(a) The horizontal distance from the base can be obtained using the equation $x=v_0\,t$, where $t$ is the time from the base to the desired point.
The time between throwing and landing points is called total flight time $T$ and can be obtained using $\Delta y=-\frac 12\,g\,t^2$. Thus, we have \begin{align*} \Delta y&=-\frac 12\,g\,t^2 \\ -24&=-\frac 12 \,(9.8)\,T^2 \\ &=2.21\,{\rm s} \end{align*} Now, substituting this value into the equation for horizontal distance, we have: \begin{align*} x&=(v_0\,\cos \theta)\,t\\ &=(8\times \cos 0)\,(2.21)\\ &=17.68\,{\rm m} \end{align*}
(b) The velocity components of the projectile just before hitting the ground are \begin{align*} v_{x}&=v_0=8\,{\rm m/s} \\ v_y&=-gT=-9.8\times 2.21 \\ &=-21.7\,{\rm m/s}\\ \\ \text{speed}&=\sqrt{v_x^2 + v_y^2}\\ &=\sqrt{8^2 + (21.7)^2}\\ &=23.12\,{\rm m/s}\\ \\ \text{direction}\quad \theta &=\tan^{-1}\left(\frac{v_y}{v_x}\right)\\&=\tan^{-1}\left(\frac{-21.7}{8}\right)\\ &=-69.7^\circ \end{align*} The negative sign indicates that the angle is below the positive $x$-axis.
Example (4): A pirate ship is $560\,{\rm m}$ away from a fort defending a harbor entrance-level defense cannon level fires balls at an initial velocity of $82\,{\rm m/s}$ at an angle of $63^\circ$. (a) How long is the cannonball in the air? (b) What is the maximum height reached by the ball?
Solution: Given the following data: the maximum distance that the cannonballs hit the ships, which is $\Delta x=560\,{\rm m}$, initial velocity $v_0=82\,{\rm m/s}$, and the angle made by the cannon with the horizontal is $63^\circ$.
(a) We can calculate the total time that the cannonballs are in the air using the equation: \begin{align*} \Delta y&=-\frac 12 gt^2 +\left(v_0 \sin \theta \right)t\\ 0&=-\frac 12 (9.8)t_T^2 +(82\times \sin 63^\circ)t_T \end{align*} Solving this equation, we find that $t_T=14.91\,{\rm s}$.
(b) When the vertical component of the projectile’s velocity is zero, denoted as $v_y=0$, it means that the projectile is at the highest point in its parabolic trajectory.
We can use the following kinematics equation for displacement in the vertical direction to find this highest point. \begin{gather*} v_y^2-v_{0y}^2 =2(-g)\Delta y \\ v^2 - (v_0 \sin \theta)^2 =2(-g)\Delta y \\ 0-(82\times \sin 63^\circ)^2 =2(-9.8)H \\ \Rightarrow \quad \boxed{H=272.3\,{\rm m}} \end{gather*}
Problem (5):
A soccer ball is kicked at $35^\circ$ above the horizontal, it lands $13.8\,{\rm m}$ away and reaches a maximum height of $2.42\,{\rm m}$.
a) What is the initial vertical velocity?
b) How long does it take to hit the ground?
c) What is the initial horizontal velocity?
d) With what velocity was the ball initially kicked ($\vec{v}$)?
Solution:
Known: $\theta=35^\circ$, Range of projectile $R=13.8\,{\rm m}$, Maximum height $H=2.42\,{\rm m}$.
(a) Recall that in projectile motion problems, there are two motions and consequently two accelerations and velocities.
Motion along the horizontal direction is uniform ($a_x=0$) and in the vertical direction is freely falling ($a_y=-g$).
Velocity is a vector quantity, so its components at the launching point are $v_{0x}=v_0 \cos \theta$ and $v_{0y}=v_0 \sin \theta$.
In this part $v_{0y}$ is unknown. Thus, either first, find the initial velocity of $v_0$ and then its vertical component or use the data for maximum height.
Recall that the projectile range is determined by \[R=\frac{v_0^2 \sin 2\theta}{g}\] After substituting the given data into it, we get \begin{align*} 13.8 &= \frac{v_0^2 \sin 2\times 35^\circ}{9.8}\\ \Rightarrow v_0 &=11.99\, {\rm m/s} \end{align*} Therefore, \begin{align*} v_{0y}&=v_0 \sin \theta\\ &=(11.99)(\sin 35^\circ)\\ &=6.87\,{\rm m/s} \end{align*} Or using the maximum height, we have \begin{align*} v_y^2 -v_{0y}^2 &=2(-g)\Delta y\\ \\ 0-v_{0y}^2 &=-2(9.8)(2.42)\\ \\ \Rightarrow v_{0y} &= 6.87\,{\rm m/s} \end{align*}
(b) The initial and final points of the projectile are at the same level, i.e., $\Delta y=0$. So by setting this into the following kinematics equation along the vertical direction, we obtain \begin{align*} \Delta y &=-\frac 12 gt^2 +\underbrace{v_0 \sin \theta}_{v_{0y}} t\\ 0&=-\frac 12 (9.8)t_T^2 +(6.87) t_T \end{align*} Thus, the time of flight is $t_T=1.40\,{\rm s}$.
(c) In projectiles, the horizontal component of initial velocity appears in the uniform motion along the horizontal direction as $\Delta x=v_{0x} t$, where $\Delta x$ is the horizontal distance. When the total time of flight is substituted for $t$, then $\Delta x$ equals the range of the projectile.
In this part, $v_{0x}$ is requested so
\begin{align*} \Delta x &= R=v_{0x} t_T \\ \\ 13.8 &= v_{0x} (1.40)\\ \\ \Rightarrow v_{0x} &=\frac{13.8}{1.4}=9.85\,{\rm m/s} \end{align*}
(d) By knowing the vertical and horizontal components of the projectile’s velocity, we can find the resultant velocity vector bellow \begin{align*} \vec{v}&=\sqrt{v_{0x}^2 +v_{0y}^2}\\ &=\sqrt{(9.85)^2+(6.87)^2}\\ &\approx \boxed{12\,\rm m/s} \end{align*} Note: the horizontal component of projectile's velocity is always the same throughout the projectile path.
Summary:
In this short course, we illustrate the application of projectile motion formulas by solving some simple examples.
Practice more problems - Kinematics in Two Dimensions.
Last reviewed: Sep 7, 2024
Author: Dr. Ali Nemati

 kinematic
kinematic
 Electrostatic
Electrostatic
 Magnetism
Magnetism