- Home
- Physics Problems
- Problems
Solved Problems
A small block is placed at height h on a frictionless, $30{}^\circ $ ramp. Upon being released (from rest), the block slides down the ramp and then falls 1 m to the floor. A small hole is located 1 m from the end of the ramp. From what height $h$ should the block be released in order to land in the hole?
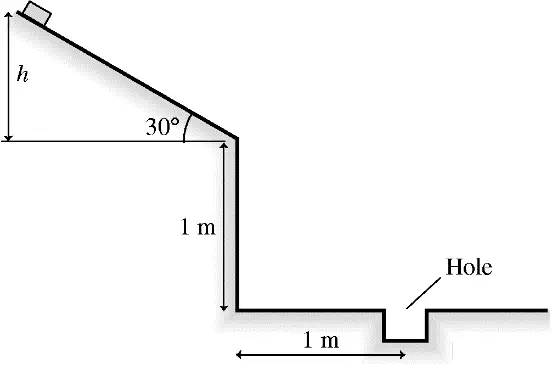
First, find the speed of the block at the bottom of ramp (from conservation of energy):
\begin{gather*} U_i+K_i=U_f+K_f \\\\ \to\quad mgh=\frac{1}{2}mv^2_1\\\\ \to\quad v_1=\sqrt{2gh}\end{gather*} In the end of the ramp, block moves in two direction (a projectile motion in a plane):
The horizontal distance that the block hits the ground to the base is given by ${\Delta }x=v_{1x}t+\frac{1}{2}a_xt^2$ but in $x$ direction there is a uniform motion i.e. $a_x=0$, so $t=\frac{\Delta x}{v_{1x}}=\frac{\Delta x}{v_1\,{\cos \theta}}$. We know that in the projectile motions the time traveled in the horizontal direction is equal to that in vertical direction. Then, \begin{align*} \Delta y &=v_{1y}t+\frac{1} {2}a_yt^2\\ &=v_1\,{\sin \theta}\frac{\Delta x}{v_1\,{\cos \theta}}+\frac{1}{2}(-g){\left(\frac{\Delta x}{v_1{\cos \theta}}\right)}^2\\\\\Rightarrow \quad \Delta y&=\Delta x\,{\tan \theta}-\frac{g(\Delta x)^2}{2v^2_1\,\cos ^{2}\theta} \end{align*} Solving for $v_1$, we get \begin{gather*} \frac{g(\Delta x)^2}{2v^2_1\,\cos^{2}\theta}=\Delta x\,{\tan \theta}-\Delta y\\ \Rightarrow \quad v^2_1=\frac{g(\Delta x)^2}{2\cos^{2}\theta \left(-\Delta y+\Delta x\,{\tan \theta}\right)}=2gh \end{gather*} Then the desired height is obtained as
\[h=\frac{(\Delta x)^2}{4\cos^{2}\theta (-\Delta y+\Delta x\,\tan \theta)}\]
Consider the end of the ramp as the origin of coordinate system, so the coordinate of the landing point is $(x=1\rm{m,y=-1m)}$ and since the block exit the ramp at $30{}^\circ$ below the horizontal so $\theta =-30{}^\circ $. Substituting these values into the above relation for $h$, we obtain \begin{align*} h&=\frac{1^2}{4\cos^{2} (-30^\circ)\left[-(-1)+1\,\tan(-30^\circ)\right]}\\&=0.788\quad {\rm m}\end{align*}
A baseball is thrown from the ground into the air with an initial velocity $\vec{v}=20\, \hat{i}+10\, \hat{j}\,{\rm m/s}$
(a) To what maximum height will the ball rise?
(b) What will be the total horizontal distance traveled by the ball?
(c) What is the velocity of the ball the instant before it hits the ground?
(a) Given the velocity, we can determine the launch angle and the magnitude of the initial velocity. \begin{gather*} \alpha={{\tan}^{-1} \frac{v_y}{y_x}}={{\tan}^{-1} \left(\frac{10}{20}\right)}=26.5{}^\circ\\\\ v_0=\sqrt{{10}^2+{20}^2}=22.36\,{\rm m/s} \end{gather*} To find the maximum height of the projectile, we must calculate the moment that the vertical component of velocity is zero $v_y=0$ \begin{gather*} v_y=v_0\,{\sin 26.5{}^\circ}-gt=0\\\\ \Rightarrow t=\frac{v_0\,{\sin 26.5{}^\circ}}{g}=\frac{22.36\times 0.44}{9.8}=1.01\, {\rm s} \end{gather*} Next, substitute it into the vertical distance relation below \begin{align*} y&=-\frac{1}{2}gt^2+v_0t\,{\sin \alpha}+y_0\\ &=-\frac{1}{2}(9.8)(1.01)^2+22.36(1.01){\sin 26.5{}^\circ}+0\\ &=5.07\quad {\rm m} \end{align*}
Alternative solution: without finding the angle and magnitude of the velocity we can find the maximum height! \begin{gather*} \vec{v}=\underbrace{20}_{v_{0x}}\hat{i}+\underbrace{10}_{v_{0y}}\hat j\,{\rm m/s}\\ v_y=v_{0y}-gt=0\\\\ \Rightarrow t=\frac{v_{0y}}{g}=\frac{10}{9.8}=1.01\, \rm{s}\end{gather*} And \begin{align*} y&=-\frac{1}{2}gt^2+\underbrace{v_0\,{\sin \alpha}}_{v_{0y}}t+y_0\\&=-\frac{1}{2}(9.8)(1.01)^2+10(1.01)+0\\ &=5.10\quad \rm{m} \end{align*} Small difference between the two results is due to uncertainty in the magnitude of the angle and initial velocity of the projectile.
(b) To find the horizontal distance, calculate the total flight time and then put it in the $x$ relation.
For finding the total flight time, substitute the location of hitting the projectile to the ground into $y=-\frac{1}{2}gt^2+v_{0y}t+y_0$. Because the launching and landing points are at the same level (choose this point as the origin $x_0=y_0=0$) and set $y=0$.
\begin{gather*} 0=-\frac{1}{2}(9.8)t^2_{tot}+10\,t_{tot}+0\\\\ \Rightarrow t_{tot}(9.8\ t_{tot}-20)=0 \\\\ \Rightarrow t_{tot}=\left\{ \begin{array}{rcl} 0\ & , & \ \ \rm{initial\ time} \\\frac{20}{9.8} & = & 2.04\ \rm{s\ ,\ \ landing\ time} \end{array} \right.\\\\ x=v_0\, {\cos \alpha}t=v_{0x}t \\\\ \Rightarrow R=x_{tot}=v_{0x}t_{tot}=20\times 2.04=40.8\, {\rm m}\end{gather*}
This is the maximum distance traveled in the horizontal direction or range of the projectile.
(c) First substitute the total flight time into the $v_y$ and $v_x$ \begin{align*}v_x&=v_{0x}=20\quad {\rm m/s}\\\\v_y&=v_{0y}-gt_{tot}\\&=10-(9.8)(2.04)\\&=-9.992\quad {\rm m/s}\end{align*} Next, the magnitude of the velocity vector is \begin{align*}v&=\sqrt{v^2_x+v^2_y}\\\\&=\sqrt{(20)^2+(-9.992)^2}\\\\&=22.35\quad {\rm m/s}\end{align*}
A particle is constrained to travel in a plane so that its position is described by
\[\vec{r}=\ \left(17\frac{m}{s^2}\right)t^2 \rm \hat i+\ \left[\left(20\frac{m}{s}\right)t\ -\ \left(6\frac{m}{s^4}\right)t^4\right]\hat{\mathrm{j}}\]
(a) Consider the motion of the particle during the time interval from $t=0\,{\rm s}$ to $t=5\,{\rm s}$? What are the displacement, average velocity and average acceleration over this time interval.
(b) Find the position, velocity and acceleration at $t=8\,{\rm s}$.
(a) Displacement of an object as it moves from an initial position $\vec r_1$ to a final position $\vec r_2$ is defined as $\Delta \vec r=\vec r_2-\vec r_1$. Thus, we must first find the position of the particle in the $0\,{\rm s}$ and $5\,{\rm s}$, next substitute them in the $\vec{r}(t)$ so \begin{align*}\vec{r}(t=5)&=(17)5^2\,\hat i+\left[(20)(5)-(6)(5)^4\right]\,\hat j\\ &=425\,\hat{i}+(100-3750)\,\hat{j}\\\\&=425\,\hat{i}-3650\,\hat{j}\quad {\rm m} \end{align*} And time $t=0$, the position vector is \begin{align*}\vec{r}(t=5)&=(17)(0)^2\,\hat i+\left[(20)(0)-(6)(0)^4\right]\,\hat j\\ &=0 \end{align*} Therefore, the difference between positions is \begin{align*}\Delta \vec{r}&={\vec{r}}_2\left(t=5\,{\rm s}\right)-{\vec{r}}_1\left(t=0\right)\\&=425\,\hat{i}-3650\,\hat{j}\end{align*} By definition, the average velocity is $\bar{v}=\rm{\Delta }\vec{r}/\rm{\Delta }t$ therefore, \begin{align*}\bar{v}&=\frac{\Delta\vec{r}}{\Delta t}\\\\&=\frac{425\,\hat{i}-3650\,\hat{j}}{5-0}\\\\&=85\,\hat{i}-730\,\hat{j}\left(\frac{m}{s}\right)\end{align*}
Average acceleration is defined as $\vec{\overline{a}}=\Delta \vec{v}/\Delta t$ where $\vec{v}$ is the instantaneous velocity of the particle i.e. $\vec{v}=d\vec{r}/dt$
So first find the change in the instantaneous velocity of the particle during time interval $0$ to $5\rm{s}$ then calculate the average acceleration. \begin{align*} \vec{v}&=\frac{d\vec{r}}{dt}\\\\&=\frac{d}{dt}\left(17t^2\,\hat i+\left[20t-6t^4\right]\hat{j}\right)\\\\ &=34\,t\hat{i}+\left[20-24t^3\right]\hat{j} \end{align*} The velocity at the instant of $t=5\,{\rm s}$ \begin{gather*} \vec{v}(t=5)=34(5)\hat i+\left[20-24(5)^3\right]\,\hat j\\\\ =170\,\hat i-2980\,\hat j\left(\frac{m}{s}\right)\\\\ \Rightarrow \quad \vec{v}(t=0)=20\,\hat j\left(\frac{m}{s}\right) \end{gather*} Thus, the change in velocity is \begin{align*} \Delta\vec{v}&=\vec{v}(t=5)-\vec{v}(t=0)\\&=170\,\hat i+(-2980-20)\,\hat j\\ &=170\,\hat i-3000\,\hat j \end{align*} By definition, the average acceleration is the change of velocity over a given time interval \[\vec{\vec{a}}=\frac{\Delta \vec{v}}{\Delta t}=\frac{170\,\hat i-3000\,\hat j}{5-0}=34\,\hat i-600\,\hat j\quad {\rm m/s}\]
(b) Now we must calculate the instantaneous quantities in $t=8\rm{s}$
\begin{align*} \vec r(t=8\,{\rm s})&=(17)(8)^2 \hat i +[(20)(8)-(6)(8)^4]\hat j\\&=1088\,\hat i-24416\,\hat j \end{align*}And, \begin{align*} \vec v&=\frac{d\vec r}{dt}\\\\&=34t\,\hat i+[20-24t^3]\,\hat j\\\\&=34(8)+\left[20-24(8)^3\right]\,\hat j\\\\&=272\,\hat i-12268\,\hat j\end{align*} Therefore, the average velocity is \begin{align*}\vec a&=\frac{d\vec v}{dt}\\\\&=34\,\hat i-72t^2 \,\hat j\\\\&=34\,\hat i-72(8)^2\,\hat j\\\\&=34\,\hat i-4608\,\hat j\end{align*}
The position of a particle as a function of time is given as:
\[\vec{r}\left(t\right)=R\,{\cos \omega t\ }\,\rm\hat i+R\,{\sin \omega t\ }\]
Determine:
(a) Instantaneous velocity vector, $\vec{v}(t)$
(b) The angle between $\vec{r}\left(t\right)$ and $\vec{v}(t)$
(c) Instantaneous acceleration vector
(d) What is the mathematical relation between $\left|\vec{a}\right|$ and $\left|\vec{v}\right|$?
(e) Using this relation (in part d), comment on the nature of this motion.
(a) Using the definition of the instantaneous velocity, we have $\vec{v}(t)=\frac{d\vec{r}}{dt}=-\hat{x}\ R\omega {\sin \omega t}+\hat{y}\ R\omega {\cos \omega t}$
(b) The angle between two vectors $\vec{A}$ and $\vec{B}$ is defined as ${\cos \alpha}=\frac{\vec{A}\cdot\vec{B}}{|A||B|}$. First, compute the inner product of them as below: \begin{align*} \vec{r}(t)\cdot\vec{v}(t) &=\left(R{\cos \omega t}\hat{x}+R{\sin \omega t}\hat{y}\right)\cdot \left(-\hat{x}\ R\omega \,{\sin R\omega}+\hat{y}\ R\omega \,{\cos R\omega}\right)\\ & =-R^2\omega \,{\sin \omega t\ }\,{\cos \omega t\ }\left(\hat{x}\cdot\hat{x}\right)+R^2\omega \,{\sin \omega t}{\cos \omega t}\left(\hat{y}\cdot\hat{y}\right)\\ &=0 \end{align*}Thus, ${\cos \alpha}=0\Rightarrow\, \alpha =90^\circ \quad {\rm or} \quad 27^\circ$
(c) $\vec{a}=\frac{d\vec{v}}{dt}=-\hat{x}R\,{\omega }^2{\cos \omega t}-\hat{y}R{\omega}^2{\sin \omega t}$
(d) The magnitude of a vector $\vec{a}=a_x\hat{x}+a_y\,\rm\hat j$ is $\left|\vec{a}\right|=\sqrt{a^2_x+a^2_y}$. So
\begin{align*}\left|\vec{v}\right|&=\sqrt{{\left(R\omega {\sin \omega t}\right)}^2+{\left(R\omega {\cos \omega t}\right)}^2}\\&=R\omega \\ \\ \left|\vec{a}\right|&=\sqrt{{\left(R{\omega }^2{\cos \omega t}\right)}^2+{\left(-R{\omega}^2{\sin \omega t}\right)}^2}\\&=R{\omega}^2 \\ \\ \therefore \quad \left|\vec{a}\right|&=\frac{{\left|\vec{v}\right|}^2}{R} \end{align*}
(e) This is the defining equation for uniform circular motion. From the beginning, one can infer the nature of the circular motion from $\vec{r}\left(t\right)$ since it defines a circle!
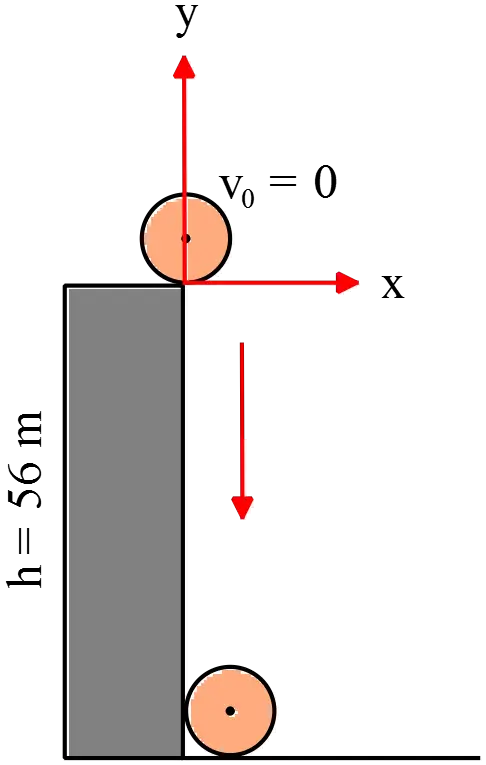
A steel ball is dropped from the top of the Leaning Tower of Pizza, which is $56\,\rm m$ high. With air resistance neglected, approximately how long does it take the ball to hit the ground?
This is a free fall problem so use the following kinematic equation to find the desired time \[y=-\frac{1}{2}gt^2+v_0t+y_0\] Where $v_0$ is the initial velocity of the ball and $y_0$ is its initial height. In all kinematic problems, we must first assume a reference point. Let the top of the tower be the origin of the coordinates so the hitting point has the coordinate $(x=0,y=-56\,\rm{m)}$. Since the ball is dropped its initial velocity is zero ($v_0=0$).\begin{gather*} y=-\frac{1}{2}gt^2+v_0t+y_0 \\\\ -56=-\frac{1}{2}(9.8)t^2+0+0 \\\\ \Rightarrow \quad t=\sqrt{\frac{2\times 56}{9.8}}=3.38\quad {\rm s}\end{gather*} In the above, $y_0=0$ because the ball was sitting on the origin initially.
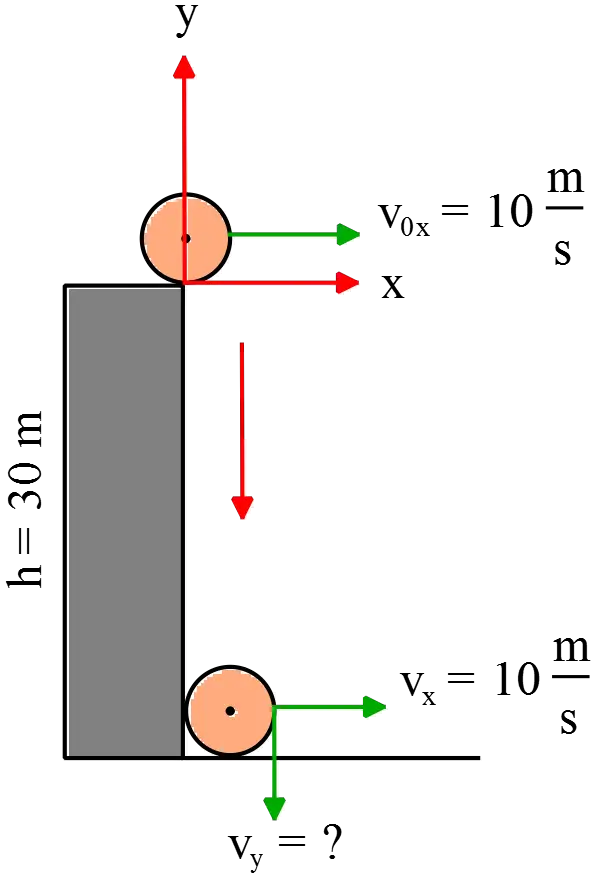
Suppose that you are climbing the Leaning Tower, and you throw your cellphone to a friend on the ground, who catches it at a point $30\ \mathrm{m}$ below the point where you released it.
You throw it straight out, with an initial horizontal velocity of $10\ \mathrm{m/s}$ (and zero initial vertical velocity). By neglecting air resistance, what is the speed of the cellphone when your friend catches it?
Find the components of the velocity at the hitting point then use the Pythagorean theorem to determine its magnitude.
Horizontal motion is uniform with speed $v_{0x}=v_x=10\,{\rm m/s}$ but vertical motion is accelerating.
In the vertical direction, we are facing a kinematic problem in one dimension.
Thus, use the time-independent kinematic equation $v^2-v_0^2=2a\Delta y$ and setting $a=-g$ to find its velocity \begin{gather*} v^2-v^2_0=2a(y-y_0)\\ \\ v^2-0=2(-9.8)(-30-0) \\ \\ \Rightarrow \quad v^2=588\quad {\rm m/s^2}\\ \\ \Rightarrow v=\sqrt{v^2_x+v^2_y}=\sqrt{{10}^2+588}=26\,{\rm m/s}\end{gather*}
A ball is thrown vertically upward with an initial speed of 20 m/s. Neglect air resistance and assume constant acceleration.
(a) How long does it take for the ball to reach its maximum height?
(b) What is that maximum height?
(c) At what height is the ball when its speed is 10 m/s?
(d) How long does it take for the ball to return to the position at which it was released?
(e) What is its speed when it returns?
(a) Given data are $v_0=20\,{\rm m/s}$ , $a=-g$ so use the following kinematic equation to find the desired time \[v=v_0-gt\] At the maximum height, the velocity of the ball is zero i.e. $v=0$. Therefore, we obtain \[0=20-9.8t \Rightarrow t=2.04\,{\rm s}\]
(b) let the starting point be the origin so $y_0=0$. Using the following kinematic equation we get \begin{align*} v^2-v^2_0&=-2g\left(y-y_0\right)\\ \\ 0-{20}^2&=-2(9.8)(y-0) \\ \\ \Rightarrow y&=\frac{400}{2\times 9.8}\\ \\&=20.4\quad {\rm m}\end{align*}
(c) Using the kinematic equation $v^2-v^2_0=-2g(y-y_0)$, we obtain \begin{align*} {10}^2-{20}^2=-2(9.8)(y-0) \\ \\ \Rightarrow y=\frac{300}{2\times 9.8}=15.3\quad {\rm m}\end{align*}
(d) Since there is no air resistance, we can multiply the result of part (a) by two and get $t_{tot}=2\times 2.04=4.08\ \mathrm{s}$ or use the relation $y=-\frac{1}{2}gt^2+v_0t+y_0$ as follows \begin{gather*} 0=-\frac{1}{2}\left(9.8\right)t^2+20t+0 \\ \\ \Rightarrow t(9.8t-40)=0 \\ \\ \Rightarrow \begin{cases} t=0 &,\text{initial time} \\ t=\frac{40}{9.8}=4.08\, {\rm s} &,\text{final time} \end{cases} \end{gather*}
(e) Use the kinematics equation $v^2-v^2_0=-2g(y-y_0)$, between the throwing and landing points \begin{gather*} v^2-v^2_0=-2g(y-y_0) \\ \\ \Rightarrow v^2-{20}^2=-2\times 9.8\times (0-0) \\ \\ \Rightarrow \quad v=20\quad {\rm m/s}\end{gather*}
A boat traveling at 12 miles/hr goes due east for $30$ minutes and then turns $45{}^\circ $ toward the north and travels another 20 minutes.
(a) What total distance does the boat travel?
(b) What is the magnitude of its displacement?
(c) What is the direction of its displacement?
(d) What is the magnitude of its average velocity?
(e) What is the direction of its average velocity?
(a) The boat has constant velocity so its acceleration is zero. Therefore, use the equation of the uniform motion as $x=vt$ where $x$ is the distance traveled. The sketch of the path is shown in the following
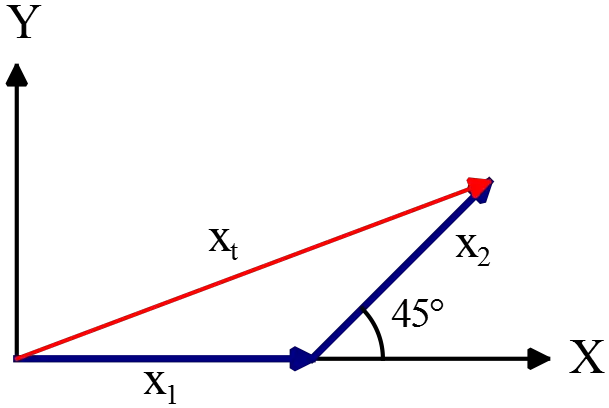
\begin{align*} x_t&=x_1+x_2\\ \\ &=v_1t_1+v_2t_2\\ \\ &={\rm \left(12\,\frac{mile}{hr}\right)\left(30\, min+20\, min\right)\left(\frac{1\, hr}{60\, min}\right)} \\ \\ &={\rm \left(12\,\frac{mile}{hr}\right)\left(\frac 12\,hr+\frac 13\,hr\right)}\end{align*}
(b) Displacement is a vector in physics whose initial position is at the first vector and its final position is at the end of the last vector. Thus, as shown in the figure $x_t$ is the displacement vector.
Use the Pythagorean theorem to find it as follows
\begin{align*} x^2_t&={\left(x_1+x_2{\cos 45^\circ}\right)}^2+{\left(x_2{\sin 45^\circ}\right)}^2\\ \\&=(6+4\cos 45^\circ)^2+(4+\sin 45^\circ)^2\\ \\ \Rightarrow \quad x_t&=\sqrt{77.94+8}\\ \\ &=9.27\quad {\rm mile}\end{align*}
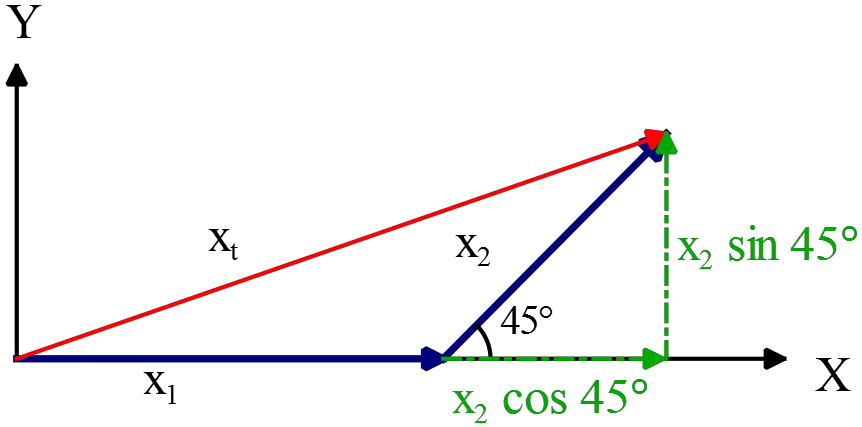
(c) The angle of the vector $\vec{R}=R_x\,\hat i+R_y\,\hat j$ with respect to the positive $x$ direction is found by $\theta =\tan^{-1}\left(\frac{R_y}{R_x}\right)$.
In the above, $\hat i$ and $\hat j$ are unit vectors along the $x$ and $y$ directions, respectively. Therefore ,\begin{align*} \tan \theta &=\frac{x_2 \sin 45^\circ}{x_1+x_2\cos 45^\circ}\\ \\ &=\frac{4\sin 45^\circ}{6+4\cos 45^\circ}\\ \\ \Rightarrow \quad \theta &=17.8^\circ\end{align*} So the resultant vector lies in the first quadrant of the coordinate system.
(d) Velocity is defined as a vector quantity in physics and defines as the displacement of the particle divided by the time interval that is $\vec{v}=\Delta \vec{x}/\Delta t$ so its magnitude is found as below \[|\vec{v}|=\frac {\text{displacement}}{\text{time}}=\frac{9.27}{\left(\frac 12+\frac 13 \right)}=11.1\,{\rm m/s}\]
(e) As we see from the definition of the average velocity, it is a vector in the direction of the displacement vector so its angle relative to the positive $x$ axis is the same as the displacement vector that is $\theta =17.8^\circ$.
A ball is thrown horizontally off the edge of a cliff with an initial speed of 15 m/s and hits the ground 3 seconds later.
(a) How high is the cliff?
(b) How far does the ball travel horizontally before it hits the ground?
(c) What is the magnitude of the ball's displacement?
(d) What is the speed of the ball when it hits the ground?
(e) At what angle from the vertical is the ball moving when it hits the ground?
(a) In the kinematics problems, first consider an origin then use the kinematics equations to find the desired parameters. Let the point of throw as the origin. This is a projectile motion.
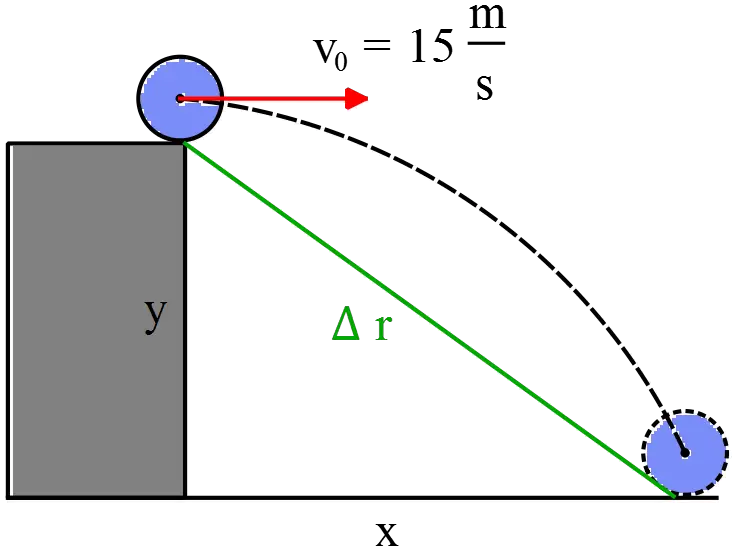
In projectile motions, the horizontal motion is under constant velocity and the vertical is under uniform acceleration $a=-g$. So in the vertical stage use the kinematics equation $y=-\frac{1}{2}gt^2+v_{0y}t+y_0$ where $y_0$ is the initial height and solve for the landing point $-y$ ( since the ball hits the ground below the origin)
\begin{gather*}-y=-\frac{1}{2}(9.8)(3)^2+0(3)+0 \\ \Rightarrow \quad y=44.1 {\rm m}\end{gather*}
(b) Use the following kinematics equation, we have $x=vt=15\times 3=45\,{\rm m}$
(c) Use the Pythagorean theorem and find the ball's displacement as shown in the figure. \begin{gather*} (\Delta r)^2=x^2+y^2={45}^2+(44.1)^2\\ =63\quad {\rm m}\end{gather*}
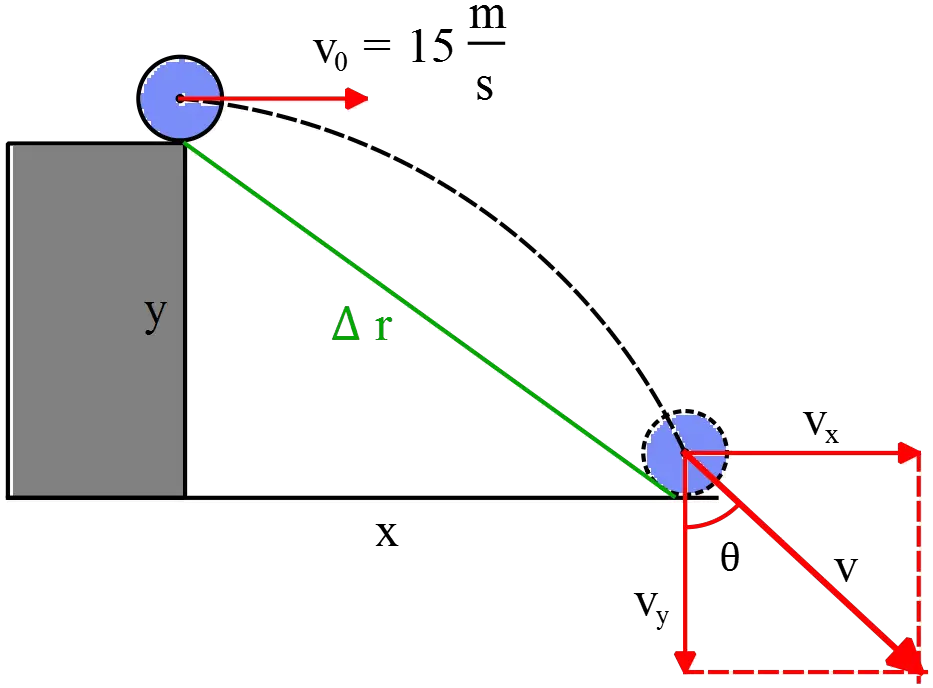
(d) First calculate its components at the moment that the ball hits the ground \begin{gather*} v=v_0+at \\ \\ \to \begin{cases} v_x=v_{0x}=15\quad {\rm m/s} \\ \\ v_y=v_{0y}-gt=0-(9.8)(3)=-29.4\,{\rm m/s} \end{cases} \end{gather*} Next, use the Pythagorean theorem to find its magnitude as follows \begin{align*}|v|&=\sqrt{v^2_x+v^2_y}\\ \\ &=\sqrt{(15)^2+(-29.4)^2}\\\\&=33\quad {\rm m/s} \end{align*}
(e) The angle with respect to the positive $x$ axis is determined by the following formula \begin{align*} \theta &={{\tan}^{-1} \left(\frac{|v_y|}{|v_x|}\right)}\\ \\& ={{\tan}^{-1} \left(\frac{15}{29.4}\right)}\\ \\ &=27.03^\circ \end{align*}Since $v_y$ is a negative number and $v_x>0$, so the final velocity directed $27.03\,^\circ$ below the +x axis.
MOST USEFUL FORMULA IN MOTION IN TWO DIMENSION:
Position vector $\vec r$ points from the origin of the coordinate system to the particle.
\[\vec r=x\hat i+y\hat j+z\hat k\]
Average velocity:
\[\vec v_{ave}=\frac{\vec r_2-\vec r_1}{t_2-t_1}=\frac{\Delta \vec r}{\Delta t}\]
Instantaneous velocity:
\[\vec v=\lim_{\Delta t \to 0} \frac {\Delta \vec r}{\Delta t}=\frac{d\vec r}{dt}\]
Average acceleration:
\[\vec a_{ave}=\frac{\vec v_2-\vec v_1}{t_2-t_1}=\frac{\Delta \vec v}{\Delta t}\]
Instantaneous acceleration:
\[\vec a=\lim_{\Delta t \to 0} \frac {\Delta \vec v}{\Delta t}=\frac{d\vec v}{dt}\]
Projectile motion:
Acceleration:
\[a_x=0 \quad , \quad a_y=-g\]
Coordinate components:
\[x=\left(v_0\,\cos \alpha\right)t \quad , \quad y=\left(v_0\,\sin \alpha \right)t-\frac 1 2 gt^2\]
velocity components:
\[v_x=v_0\,\cos \alpha\ \quad , \quad v_y=v_0\,\sin \alpha -gt\]
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
