Electric Field - Problems and Solution
This article is tailored for grade 12 and college students aiming to understand how electric charges interact through electric fields by practicing some problems and questions.
You'll discover step-by-step solutions to various problems, ensuring you grasp the concepts and applications thoroughly.
With the AP Physics 1 exam around the corner, don't miss out on downloading and reviewing this essential 31-page equation sheet—it could be your key to success! Limited time offer for just $\$ 10$! (Download free PDF sample).
Electric Field Practice Problems
Problem (1): What is the magnitude and direction of the electric field due to a point charge of $20\,{\rm \mu C}$ at a distance of 1 meter away from it?
Solution: The magnitude of the electric field due to a point charge $q$ at a distance $r$ from it is given by $E=k\frac{q}{r^2}$. Substituting the numerical values into this equation, we obtain \begin{align*} E&=k\frac{q}{r^2} \\\\ &=\frac{(9\times 10^{9})(20\times 10^{-6})}{1^2}\\ \\&=1.8\times 10^{5} \quad \rm N/C \end{align*} In the above equation, $k$ is an experimentally obtained positive constant called the Coulomb constant, whose exact value is \[k=8.99\times 10^{9} \quad {\rm \frac{N\cdot m^2}{C^2}}\] The sign of the charge determines the direction of the electric field. In this case, since the charge is positive, the electric field is directed away from it at every point.

Problem (2): Determine the magnitude and direction of the electric field at a point $2\,\rm cm$ to the left of a point charge of $-2.4\,\rm nC$.
Solution: The difference between this question and the previous one lies in the sign of the electric charge. Remember that to find the magnitude of the electric field due to a point charge at any point in space, we only need the absolute value of the charge and not its sign. Thus, the magnitude of $E$ is found as \begin{align*} E&=k\frac{q}{r^2} \\\\ &=\frac{(9\times 10^9)(2.4\times 10^{-9})}{(0.02)^2} \\\\ &=54\times 10^3 \quad \rm N/C \end{align*} In all questions related to the electric field, only the sign of the charge gives us the direction of the electric field. In this case, the charge is negative, so the direction of the electric field is toward the charge $-2.4\,\rm nC$ as shown in the figure below.

Were these not helpful? My income relies on your generous donations. Please support me.
Problem (3): Determine the magnitude and direction of the electric field at a point in the middle of two point charges of $4\,\rm \mu C$ and $-3.2\,\rm \mu C$ separated by $4\,\rm cm$?
Solution: Let the line connecting the charges be the $x$ axis, and consider right as the positive direction.
First, find the electric field due to each charge at the midpoint between them, which is located at a distance of $d=2\,\rm cm$ from each charge. The magnitude of the electric field due to a charge of $4\,\rm \mu C$ at that point can be calculated as follows: \begin{align*} E&=k\frac{q}{d^2} \\\\ &=\frac{(9\times 10^9)(4\times 10^{-6})}{(0.02)^2} \\\\ &=90\times 10^6\,\rm N/C \end{align*} Since this charge is positive, its electric field points away from it, specifically to the right.
Similarly, for a point charge $-3.2\,\rm \mu C$, we can calculate he magnitude and direction of the electric field using the same formula: \begin{align*} E&=k\frac{q}{d^2} \\\\ &=\frac{(9\times 10^9)(3.2\times 10^{-6})}{(0.02)^2} \\\\ &=72\times 10^6\,\rm N/C \end{align*} Since this charge is negative, its electric field is directed towards it, specifically along the positive $x$-axis.
Next, we can use the superposition principle to find the net electric field at our desired point. According to this principle, the total electric field at a point is obtained by taking the vector sum of individual fields due to each charge. Therefore, \begin{align*} \vec{E}_{net}&=\vec{E}_1+\vec{E}_2 \\\\ &=(90+72) \times 10^6 \\\\ &=+162\times 10^6 \quad\rm N/C \end{align*} Hence, at a point midway between these charges, the magnitude of the electric field is found to be $162\times 10^6\,\rm N/C$ and its direction is to the right or towards the negative charge, as shown in the figure.
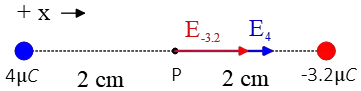
Understand more about the electric charge concept by solving these practice problems on electric charge.
Problem (4): In the vicinity of point charge $q$, we place a $0.2\,{\rm \mu C}$-charge so that a force of $5\times 10^{-5}\,{\rm N}$ applied to it due to the charge $q$. Find the electric field produced by this unknown charge $q$.
Solution: The Coulomb force exerted on a test point charge $q_0$ at any point is related to the electric field (due to an unknown charge $q$) at that point by \[\vec{F}=q_0\vec{E}\]Therefore, the magnitude of the electric field is obtained as \begin{align*}E&=\frac{F}{q_0}\\ \\ &={\rm \frac{5\times 10^{-5}\,N}{0.2\times 10^{-6}\,C}}\\ \\&= 250\quad {\rm \frac NC}\end{align*}
The electric field problems are closely related to Coulomb's force problems.
Problem(5): An electron is released from rest in a uniform electric field of magnitude $E=100\,{\rm N/C}$ and gains speed.
(a) Find the magnitude of the force applied to it.
(b) After traveling a distance of $1$ meter, how fast does it reach?
Solution: The magnitude of the charge of an electron is $e=1.6\times 10^{-19}\,{\rm C}$, and the electron mass is $m_e=9.1\times 10^{-31}\,{\rm kg}$.
(a) The electric field and electric force are related by the formula $F=qE$. Therefore, we can calculate the force as follows: \begin{align*}F&=qE\\&=(100)(1.6\times 10^{-19})\\&=1.6\times 10^{-17}\quad {\rm N}\end{align*}
(b) Given that the force on the electron is $1.6\times 10^{-17}\,\rm N$ and the mass of the electron is known, we can use Newton's second law $F=ma$ to find the acceleration $a$ of the electron: \begin{align*} a&=\frac{F}{m} \\\\ &=\frac{1.6\times 10^{-17\,\rm N}}{9.1\times 10^{-31}\,\rm kg} \\\\ &= 1.76\times 10^{13}\,\rm m/s^2\end{align*} Then, we can use the kinematic equation $v^2-v_0^2=2ax$ to find the final speed $v$ of the electron after it has traveled one meter ($x=1\,\rm m$) through the electric field: \begin{align*} v^{2}&=2\left(\frac{F}{m}\right)x+v_0^{2}\\ \\ &=2(1.76\times 10^{13})\times (1)\\ \\ &=0.35\times 10^{14}\end{align*} Remember, “from rest” means the initial velocity $v_0$ is zero. So, you can substitute $a$ and $x$ into the equation to find $v$.
This part is related to a problem on kinematics. Refer to that page and solve more problems.
Problem (6): What is the force on an electron at a point where the electric field is $\vec{E}=5\times 10^{5}\,(\hat{i})\,{\rm N/C}$.
Solution: electric force $\vec{F}$ on a test point charge $q_0$ and electric field $\vec{E}$ is related by $\vec{F}=q_0 \vec{E}$. Thus, the electric force is \begin{align*} \vec{F}&=-e \vec{E}\\ &=-\left(1.6\times 10^{-19}\right)\left(5\times 10^{5}\,\hat{i}\right)\\&=-8\times 10^{-14}\,\hat{i}\quad {\rm N}\end{align*} Where $q_0$ is replaced by the electron charge which has a negative value, i.e., $q_0=e=-1.6\times 101^{-19}\,{\rm C}$. Thus, the force is toward the negative $x$-axis.
Problem (7): The electric field due to charges $q_1=2\,\rm {\mu C}$ and $q_2=32\,\rm {\mu C}$ at a distance $16\,\rm {cm}$ from charge $q_2$ is zero. What is the distance between the two charges?
Solution: Since the two charges $q_1$ and $q_2$ are positive, somewhere between them, the net electric force must be zero; that is, at that point, the magnitudes of the fields are equal (remember that the electric field of a positive charge at the field point is outward). Therefore, we get \[\vec E_{net}=0 \quad \Longrightarrow \quad |\vec E_1|=|\vec E_2|\]

Now, use the definition of an electric field to compute the electric fields at that point due to the two charges as follows: \[k\frac{|q_1|}{r_1^2}=k\frac{|q_2|}{r^{2}} \quad \Longrightarrow \quad \frac{2}{x^{2}}=\frac{32}{16^{2}}\] Taking the square root of both sides, we obtain \[\frac{1}{x}=\frac{4}{16} \quad \Longrightarrow \quad x=4 \rm {cm}\]
As shown in the figure, the distance between the two charges is $d=x+16=4+16=20\, \rm {cm}$.
Problem (8): Three point charges are located at the corners of an equilateral triangle, as depicted below. Find the electric field at a point midway between the two charges placed on the $x$-axis.
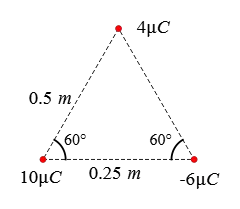
Solution: An equilateral triangle is a triangle that has all sides and angles equal. In this question, we are asked to find the net electric field midway on the $x$-axis.
The calculation of the magnitude of the electric field at a point between the charges on the $x$-axis is straightforward. To find the electric field due to the charge $\rm 4\,\mu C$, we need to determine the distance to the desired point.
According to the Pythagorean theorem, we can find this distance, denoted as $c$, as follows: \begin{align*} c&=\sqrt{a^2-b^2} \\\\ &=\sqrt{(0.5)^2-(0.25)^2} \\\\ &=0.43\,\rm m \end{align*} The electric field due to a charge of $10\,\rm \mu C$ at point $P$ is given by \begin{align*} E_{10}&=k\frac{q}{r^2} \\\\ &=\frac{(9\times 10^9)(10\times 10^{-6})}{(0.25)^2} \\\\ &=1.44\times 10^6 \,\rm N/m \end{align*} Since the charge is positive, the electric field is directed to the right. Similarly, for a charge of $-6\,\rm \mu C$, we have: \begin{align*} E_{-6}&=k\frac{q}{r^2} \\\\ &=\frac{(9\times 10^9)(6\times 10^{-6})}{(0.25)^2} \\\\ &=0.86\times 10^6 \,\rm N/m \end{align*} The charge is negative, so its electric field at point $P$ is directed to the right. Finally, for a charge of $4\,\rm \mu C$, we have: \begin{align*} E_{4}&=k\frac{q}{r^2} \\\\ &=\frac{(9\times 10^9)(4\times 10^{-6})}{(0.43)^2} \\\\ &=0.19\times 10^6 \,\rm N/m \end{align*} Since the charge is positive, its electric field at point $P$ is directed away from it, i.e., downward.
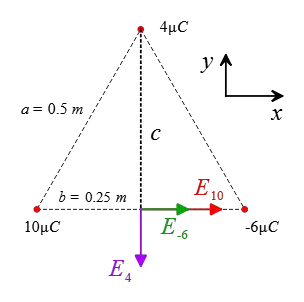
Therefore, along the positive $x$-direction, there are two forces that add together and make the $x$-component of the net electric field at point $P$, \[E_{net-x}=(0.86+1.44) \times 10^6 =2.30\times 10^6 \,(\hat{i})\quad\rm N/m \] The $y$-component of the net electric field is the same field due to the single charge $4\,\rm \mu C$ downward: \[E_{net-y}=-0.19\times 10^6 \,(\hat{j}) \quad \rm N/m\] The magnitude of the $E_{net}$ at point $P$ is the calculated as follows: \begin{align*} E_{net}&=\sqrt{E_x^2+E_y^2} \\\\ &=\sqrt{(2.30)^2+(-0.19)^2} \\\\ &=2.31\times 10^3\,\rm N/m \end{align*}
If you are getting ready for the AP Physics C exam, these problems on the electrostatic force are also relevant.
Problem (9): In the following figure, there are two point charges separated by a distance of $1.0\,\rm m$. Find a point other than infinity where the net electric field due to these charges is zero.
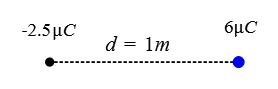
Solution: Remember that the direction of the electric field at a distance $r$ from a point charge depends on the sign of its charge. For positive charges, the electric field points radially outward at the desired point, and for negative charges, it points radially inward.
Now, let's examine an arbitrary location on the line connecting the charges.
Assume a point between the charges where the electric field due to each charge points to the left, so the net electric force cannot be zero.
Next, consider a point outside the charges, for example, close to the larger charge $\rm 6\,\mu C$ at a distance $x$ from it. At this point, the electric fields point in opposite directions, so there is a possibility to cancel each other.
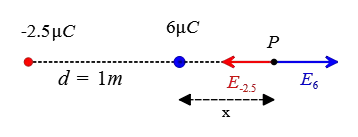
\begin{gather*} E_6 = E_{-2.5} \\\\ k\frac{q_6}{x^2} =k\frac{q_{2.5}}{(d+x)^2} \\\\ \frac{6\times 10^{-6}}{x^2}=\frac{2.5\times 10^{-6}}{(1+x)^2} \\\\ \rightarrow 6(1+x)^2=(2.5)x^2 \\\\ \Rightarrow \boxed{3.5x^2+12x+6=0} \end{gather*} The solutions of this quadratic equation are \[x_1=-2.8\,{\rm m} \quad x_2=-0.6\,\rm m\] The negative solution here means that our chosen point must be located either between the charges, $0<x_2<1$, which is ruled out by the initial reasoning, or outside the charges and close to $-2.5\,\rm \mu C$ at a distance $x=1.8\,\rm m$ from it, as shown in the figure below.
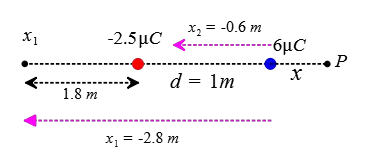
Therefore, as a rule of thumb, in all the electric field questions like this one, the net electric field due to two unlike charges somewhere outside the charges and close to the smaller charge becomes zero.
Somewhere off the horizontal axis, the electric field due to each point charge makes an angle with each other, so it is not possible to find a point where the net electric field is zero.
To have a better understanding of vectors and their properties, refer to the page below:
Vectors, definitions, formulas, and solved problems
Problem (9): In the figure, three equal charges $q_1=q_2=q_3=+4\, \rm {\mu C}$ are located on the perimeter of a sphere of diameter $12\, \rm {cm}$. Find the net electric field in terms of unit vectors $\hat i,\hat j$ at the sphere's center.
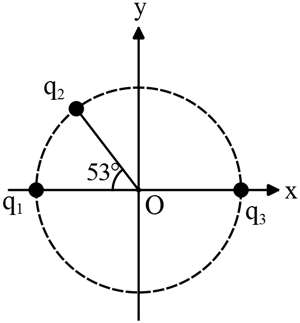
Solution:
Reasoning: The electric fields of charges $q_1$ and $q_3$ at the center of the sphere are equal in magnitude and opposite in direction. Since the magnitudes of charges are the same ($q_1=q_3$) and they are located at equal distances from the center, we can use the definition of the electric field to determine that: \[E_1=k\frac{|q_1|}{r^2}=E_3 \quad, \quad \vec E_1=-\vec E_3\] Therefore, the resultant electric field vector at point $\rm O$ is equal to the field $\vec E_2$, using the superposition principle of fields: \[\vec E_{net,O}=\underbrace{\vec E_1+\vec E_3}_{0}+\vec E_2=\vec E_2\] However, the electric field $\vec E_2$ lies in the fourth quadrant along the radius of the sphere, making an angle of $53^\circ$ relative to the $+x$ axis as shown in the figure. In such cases, we must decompose the vector into its components in $x$ and $y$ directions.
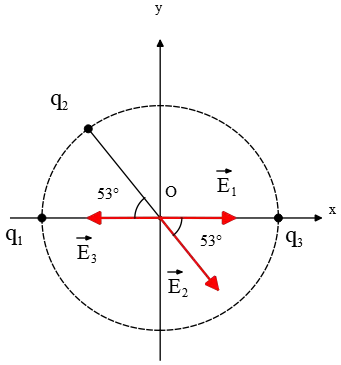
First, use the definition of the electric field of a point charge to find the magnitude of $\vec E_2$ as: \begin{align*} \vec E_2&=k\frac{|q_2|}{r^{2}}\\ &=\left(9\times 10^{9}\, \rm {N \cdot \frac{m^2}{C^2}}\right)\frac{4\times 10^{-6}\, \rm C}{\left(\frac{12}{2}\times 10^{-2}\,\rm{m}\right)^2}\\ &=10^{7}\, \rm{\frac{N}{C}} \end{align*} Next, we can decompose the vector $\vec E_2$ using elementary geometry as follows: \begin{align*} \vec E_2&=\underbrace{|\vec E_2|\,\cos 53^\circ}_{E_{2x}}\left(\hat i\right)+\underbrace{|\vec E_2|\,\sin 53^\circ}_{E_{2y}}\left(-\hat j\right)\\ \\ &=10^{7}(0.6)\left(\hat i\right)+10^{7}(0.8)\left(-\hat j\right) \end{align*} By factoring and rearranging the above relation, we get:
\begin{align*} \vec E_2&=10^{7}\left(0.6 \hat i-0.8 \hat j\right)\\ &=6 \times 10^{6} \hat i-8\times 10^{6} \hat j \quad \left({\rm \frac NC}\right)\end{align*}
Problem (10): As shown in the figure, the two charges $q_1$ and $q_2$ are fixed at the corners of the lower side of an isosceles triangle. If the electric field vector at point $A$ (in SI) is $\vec E_A=\left(7.2 \times 10^{4}\right)\hat i$, determine the type and magnitude of electric charges $q_1$ and $q_2$.
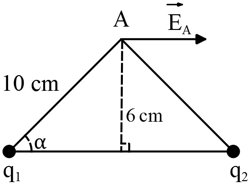
Solution: The solution is straightforward. We can use the superposition principle to find two relationships between the magnitudes of charges. Therefore, we have:
\begin{align*}\vec E_A&=\vec E_1+\vec E_2 \\ \vec E_A&=k \frac{|q_1|}{r_1^2}\hat r_1+k \frac{|q_2|}{r_2^2}\hat r_2 \end{align*} In the second equality, we have used the formula of the electric field of a point particle.
The unit vectors $\hat{r}$ are in arbitrary directions since we do not have any knowledge about the charges being positive or negative. We need to find these unit vectors as we proceed. (Recall the unit vectors problems to better understand these types of vectors.)
By decomposing the unit vectors in the $x$ and $y$ directions and noting that in an isosceles triangle $r_1=r_2=d$, we can simplify further:

\begin{align*} \vec E_A&=\frac{k}{d^{2}}{|q_1|\left(\cos \alpha\, \hat i+\sin \alpha\, \hat j\right)+|q_2|\left(\cos \alpha \left(-\hat i\right)+\sin \alpha\, \hat j\right)}\\ \\ &=\frac{k}{d^2}{\cos \alpha\, \left(|q_1|-|q_2|\right)\hat i+\sin \alpha\, \left(|q_1|+|q_2|\right)\hat j}\end{align*} To decompose the unit vectors we have assumed the charges are positive.
Since the electric field at point $A$ is in the positive $x$ direction, the $j$ component of the right-hand side of the above equation must vanish, and its $i$ components must be equal to the left part, as shown below: \begin{gather*} \vec E_A=\frac{k}{d^2}\,{\cos \alpha \left(|q_1|-|q_2|\right)\hat i+\underbrace{\sin \alpha \left(|q_1|+|q_2|\right)}_{0}\hat j}\\ \\ |q_1|+|q_2|=0\\ \\ 7.2\times 10^{4}=\frac{k}{d^2}\, \cos \alpha\, \left(|q_1|-|q_2|\right) \end{gather*} The first expression states that the magnitudes of the charges are opposite each other, i.e., $|q_1|=-|q_2|$. From the second equation, one can find: \begin{gather*} 2|q_1|\frac{k}{d^2}\,\cos \alpha =7.2\times 10^{4}\\ \Longrightarrow |q_1|=3.6\times 10^{4} \frac{d^2}{k\,\cos \alpha} \end{gather*} Using the Pythagorean theorem in the left triangle to find the value of $\cos \alpha$, we have: \begin{gather*} 10^2=6^2+x^2 \quad \Longrightarrow \quad x=8\, \rm {cm}\\ \cos \alpha =\frac{8}{10} \end{gather*} By substituting the known data, we obtain: \begin{align*}|q_1|&=3.6\times 10^4 \frac{\left(10\times 10^{-2} \rm {m}\right)^{2}}{\left(9\times 10^{9}\right)\left(0.8\right)}\\ \\ &=0.5\times 10^{-9}\, \rm {C}\\ \\ &=0.5\quad {\rm {nC}} \end{align*}Thus, $|q_1|=-|q_2|=0.5\, \rm {nC}$. Our initial assumption that the charges are positive is incorrect. Therefore, we must correctly choose one of them to be positive and the other negative. By choosing $q_1$ to be positive and $q_2$ to be negative, we can arrive at the right net electric field at point $A$.
Problem (11): In the figure below, a point particle with a mass of $20\,{\rm g}$ and charge of $-3\,{\rm \mu C}$ is placed into a uniform electric field produced by two charged parallel plates. If we release the particle from the lower plate, at what speed does the particle reach the upper plate?

Solution: Recall that a negatively charged particle moves in the opposite direction of the electric field lines. Two forces act on the particle: one is the electrostatic force, and the other is the gravitational force (weight).
The magnitude of the electric force acting on the particle is: \begin{align*}F&=|q|E\\&=\left(3\times 10^{-6}\right)\left(2\times 10^{5}\right)\\&=0.6\quad {\rm N}\end{align*} The weight of the particle is: \[mg=\left(20\times 10^{-3}\right)(10)=0.2\,{\rm N}\] We can see the electric force is greater than the weight, so the particle starts moving upwards.
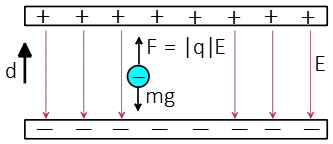
Next, we can use the kinetic-energy theorem,$\Delta K=W_t$, which you learned in the section on work-kinetic energy problems, to find the particle's speed at the upper plate. $W_t$ is the total work done on the particle, and $\Delta K$ is the difference between initial and final kinetic energies. Thus, we have: \begin{align*} W_t &=\Delta K \\ \\ W_F+W_{mg} &=\frac 12 mv_f^2-\frac 12 mv_i^2 \\ \\ Fd\,\cos \alpha + mgd\,\cos \theta&=\frac{1}{2}mv_f^2 +0 \\ \\ (0.6)(0.1)(1)+(0.2)(0.1)(-1)&=\frac 12 (20\times 10^{-3})v_f^2 \\ \\ 6\times 10^{-2}-2\times 10^{-2}&=10^{-2}v_f^2\\ \\ \Rightarrow v_f^2 &=4 \\ \\ v_f&=2\quad {\rm m/s}\end{align*} In the above, we used the definition of work as $W=Fx \cos \theta$, where $x$ is the displacement vector and $\theta$ is the angle between the force and displacement.
In the third equality, $\alpha$ and $\theta$ are the angles between electric force $F$ and the weight $mg$ force with displacement $d$, respectively.
Refer to this section to solve more problems on work in physics.
Problem(12): The electric potential difference between two parallel plates $2.4\,\rm cm$ apart is $240\,\rm V$. What is the magnitude of the electric field between them?
Solution: The electric potential difference $\Delta V$ between two points where a uniform electric field $E$ exists is related by: \[E=\frac{\Delta V}{d}\] where $d$ is the distance between those points.
Substituting the numerical values, we have: \[E=\frac{240\,\rm V}{0.024\,\rm m}=10000\,\rm V/m\] Note that the volt per meter ($\rm V/m$) is another unit for the electric field.
You can find more problems about electric potential here.
Author: Dr. Ali Nemati
Last Update: Nov 22, 2022
© 2015 All rights reserved. by Physexams.com
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
