Master Kinematics: Solved Problems and Explanations
Struggling with kinematics problems? Do you want to understand the principles of motion clearly and concisely? Look no further! Our comprehensive guide on “Kinematics Problems” is here to help.
Whether studying for an exam or working on homework, these solutions offer a practical approach to understanding and applying kinematics equations.
All kinematics equations are summarized in the following expressions: \begin{gather*} \Delta x=\frac{v_1+v_2}{2}\times \Delta t \\\\ v=v_0+at \\\\ \Delta x=\frac 12 at^2+v_0t \\\\ v^2-v_0^2=2a\Delta x \end{gather*}
Save time, boost your AP Physics 1 score! Get our 31-page comprehensive equation sheet for just $\$ 10$ — A limited-time offer. (Download free PDF sample).
Kinematics Practice Problems:
Problem (1): A car slows its motion down from 10 m/s to 6 m/s in 2 seconds under constant acceleration.
(a) What is its acceleration?
(b) How far did the car travel during this time interval?
Solution: This is a basic kinematics problem, so we will explain the steps in detail.
Step 1: Since all these problems are in one dimension, draw a horizontal axis (like the positive $x$ axis), and place the object on it, so that its motion matches the direction of the axis.
Step 2: Specify the known and wanted information. Here, in the elapsed time interval $2\,{\rm s}$, the initial and final velocities of the car are given as $v_i=10\,{\rm m/s}$ and $v_f=6\,{\rm m/s}$. The wanted quantity is the constant acceleration of the object (car), $a=?$.
Step 3: Apply the kinematics equation that is appropriate for this situation.
(a) To find the acceleration in this problem, we are given the time, initial, and final velocity. The kinematics equation $v=v_0+at$ is suitable for this situation, as the only unknown variable is the acceleration $a$. By rearranging the equation, we get \begin{gather*} v=v_0+at\\\\ 6=10+a(2) \\\\ 6-10=2a \\\\\Rightarrow \quad a=\frac{6-10}{2}=-2\quad {\rm \frac{m}{s^2}}\end{gather*} Since the problem states that the acceleration is constant, we could also use any of the other constant acceleration kinematics equations. The negative sign of the acceleration indicates that it is directed toward the negative $x$ axis.
(b) "How far'' indeed refers to the distance traveled, denoted by $x$ in the kinematics equations.
Here, the best equation that relates the known and unknown information is $x=\frac 12 at^2+v_0t$ or $v^2-v_0^2=2ax$. We choose the first, so \begin{align*} x&=\frac 12 at^2+v_0t \\\\&=\frac 12 (-2)(2)^2+(10)(2) \\\\&=16\quad {\rm m}\end{align*}
Problem (2): A moving object slows down from $12\,{\rm m/s}$ to rest at a distance of 20 m. Find the acceleration of the object (assumed constant).
Solution: In the diagram below, all known information along with the direction of the uniform motion is shown.
A common phrase in kinematics problems is “ending or coming to a rest”, which means the final velocity of the object in the time interval we are considering is zero, $v_f=0$.
The kinematics equation that suits this problem is $v^2-v_0^2=2a(x-x_0)$, where the only unknown variable is the acceleration $a$.
For simplicity, we can assume the initial position of the motion $x_0$ is zero in all kinematics problems, $x_0$. \begin{gather*} v^2-v_0^2=2ax\\\\0^2-(12)^2 =2a(20) \\\\ \rightarrow a=\frac{-144}{2\times 20}\\\\\Rightarrow \boxed{a=-3.6\quad {\rm \frac{m}{s^2}}}\end{gather*} As before, the negative sign indicates of the acceleration indicates that it is directed to the left.
Problem (3): A bullet leaves the muzzle of an 84-cm rifle with a speed of 521 m/s. Find the magnitude of the bullet's acceleration by assuming it is constant inside the barrel of the rifle.
Solution: The bullet accelerates from rest to a speed of 521 m/s over a distance of 0.84 meters. We have the following known quantities: the initial velocity $v_0$,the final velocity $v$, and the displacement $x-x_0$. The unknown is acceleration $a$. The perfect kinematics equation that relates all these variables is $v^2-v_0^2=2a(x-x_0)$. Solving for $a$, we have: \begin{gather*}v^2-v_0^2=2a(x-x_0)\\\\ (521)^2-0=2(a)(0.84-0) \\\\ \Rightarrow \boxed{a=1.62\times 10^5\quad {\rm m/s^2}}\end{gather*} This calculation results in a very large acceleration.
Your donation will help us keep our physics lessons accessible to students around the world. Thank you for your support.
Problem (4): A car starts its motion from rest and uniformly accelerates at a rate of $4\,{\rm m/s^2}$ for 2 seconds in a straight line.
(a) How far did the car travel during those 2 seconds?
(b) What is the car's velocity at the end of that time interval?
Solution: "Start from rest'' means the initial object's velocity is zero, $v_0=0$. The known information are $a=4\,{\rm m/s^2}$, $t=2\,{\rm s}$ and wants the distance traveled $x=?$.
(a) Since $x$ is the only unknown quantity, we can use the kinematics equation $x=\frac 12 at^2+v_0 t+x_0$ to relate the given information. Using the known data, we can calculate $x$ as follows: \begin{align*} x&=\frac 12 at^2+v_0 t+x_0 \\\\&=\frac 12 (4)(2)^2+(0)(2) \\\\&=\boxed{8\quad {\rm m}}\end{align*} As before, we set $x_0=0$.
(b) Knowing the distance traveled by car in this time interval, we can use the following kinematics equation to find the car's final velocity $v$: \begin{align*} v^2-v_0^2 &=2a(x-x_0) \\\\v^2-(0)^2&=2(4)(8-0) \\\\v^2&=64\end{align*} Taking the square root, we get $v$: \[v=\sqrt{64}=\pm 8\quad {\rm \frac ms}\] We know that velocity is a vector quantity in physics, having both magnitude and direction.
The velocity (speed) magnitude is 8 m/s, but in what direction? Or which sign should we choose? The correct sign for velocity is positive because the car is uniformly accelerating in the positive $x$ direction without stopping.
Therefore, the car's final velocity is $\boxed{v_f=+8\,{\rm m/s}}$.
Problem (5): We aim to design an airport runway with the following specifications: The lowest acceleration of a plane should be $4\,{\rm m/s^2}$, and its take-off speed should be 75 m/s. How long would the runway have to be to allow the planes to accelerate through it?
Solution: The known quantities are acceleration $a=4\,{\rm m/s^2}$, and final velocity $v=75\,{\rm m/s}$. The wanted quantity is the runway length $\Delta x=x-x_0$. The ideal kinematics equation that relates these variables is $v^2-v_0^2=2a(x-x_0)$. \begin{align*} v^2-v_0^2&=2a\Delta x\\\\ (75)^2-0&=2(4) \Delta x\\\\ \Rightarrow \Delta x&=\boxed{703\quad {\rm m}}\end{align*} Thus, for the runway to be effective, its length must be at least approximately 703 meters.
Problem (6): A stone is dropped vertically from a high cliff. After 3.55 seconds, it hits the ground. How high is the cliff?
Solution: There is another type of kinematics problem in one dimension but in the vertical direction. In such problems, the constant acceleration is that of free falling, $a=g=-10\,{\rm m/s^2}$.
"Dropped'' or "released'' in free-falling problems means the initial velocity is zero, $v_0=0$. In addition, it is always better to consider the point of release as the origin of the coordinate, so $y_0=0$.
The most relevant kinematics equation for these known and wanted quantities is $y=-\frac 12 gt^2+v_0t+y_0$ \begin{align*} y&=-\frac 12 gt^2+v_0t+y_0 \\\\&=-\frac 12 (9.8)(3.55)^2+0+0\\\\&=\boxed{-61.8\quad {\rm m}}\end{align*} The negative indicates that the impact point is below our chosen origin.
Problem (7): A car slows down uniformly from $45\,\rm m/s$ to rest in $10\,\rm s$. How far did it travel in this time interval?
Solution: List the data known as follows: initial speed $v_0=45\,\rm m/s$, final speed $v=0$, and the total time duration that this happened is $t=10\,\rm s$. The unknown is also the amount of displacement, $\Delta x$.
The only kinematics equation that relates these together is $\Delta x=\frac{v_1+v_2}{2}\times \Delta t$, where $v_1$ and $v_2$ are the velocities at the beginning and end of that time interval. \begin{align*} \Delta x&=\frac{v_1+v_2}{2}\times \Delta t \\\\ &=\frac{45+0}{2}\times 10 \\\\ &=\boxed{225\,\rm m}\end{align*} Keep in mind that we use this formula when the object slows down uniformly, or, in other words when the object's acceleration is constant.
Problem (8): A ball is thrown into the air vertically from the ground level with an initial speed of 20 m/s.
(a) How long is the ball in the air?
(b) At what height does the ball reach?
Solution: The throwing point is considered to be the origin of our coordinate system, so $y_0=0$. Given the initial velocity $v_0=+20\,{\rm m/s}$ and the gravitational acceleration $a=g=-9.8\,{\rm m/s^2}$. The wanted time is how long it takes the ball to reach the ground again.
To solve this free-fall problem, it is necessary to know some notes about free-falling objects.
Note (1): Because the air resistance is neglected, the time the ball is going up is half the time it is going down.
Note (2): At the highest point of the path, the velocity of the object is zero.
(a) By applying the kinematics equation $v=v_0+at$ between the initial and the highest ($v=0$) points of the vertical path, we can find the going up time. \begin{align*} v&=v_0+at \\0&=20+(-9.8)t\\\Rightarrow t&=2.04\quad {\rm s}\end{align*} The total flight time is twice this time \[t_{tot}=2t=2(2.04)=4.1\,{\rm s}\] Hence, the ball takes about 4 seconds to reach the ground.
(b) The kinematics equation $v^2-v_0^2=2a(y-y_0)$ is best for this part. \begin{align*} v^2-v_0^2&=2a(y-y_0) \\0-20^2&=2(-9.8)(y-0) \\ \Rightarrow y&=\boxed{20\quad {\rm m}}\end{align*} Hence, the ball goes up to a height of about 20 meters.
Problem (9): An object moving in a straight line with constant acceleration, has a velocity of $v=+10\,{\rm m/s}$ when it is at position $x=+6\,{\rm m}$ and of $v=+15\,{\rm m/s}$ when it is at $x=10\,{\rm m}$. Find the acceleration of the object.
Solution: Draw a diagram, put all known data into it, and find a relevant kinematics equation that relates them together.
We want to analyze the motion in a distance interval of $\Delta x=x_2-x_1=10-6=4\,{\rm m}$, thus, we can consider the velocity at position $x_1=6\,{\rm m}$ as the initial velocity and at $x_2=10\,{\rm m}$ as the final velocity.
The most relevant kinematics equation that relates these known quantities to the wanted acceleration $a$ is $v^2-v_0^2=2a(x-x_0)$, where $x-x_0$ is the same given distance interval. Thus, \begin{align*} v^2-v_0^2&=2a(x-x_0) \\\\ (15)^2-(10)^2&=2(a)(4) \\\\225-100&=8a\\\\\Rightarrow a&=\frac{125}{8}\\\\&=15.6\,{\rm m/s^2}\end{align*}
Problem (10): A moving object accelerates uniformly from 75 m/s at time $t=0$ to 135 m/s at $t=10\,{\rm s}$. How far did it move at the time interval $t=2\,{\rm s}$ to $t=4\,{\rm s}$?
Solution: Draw a diagram and implement all known data in it as below.
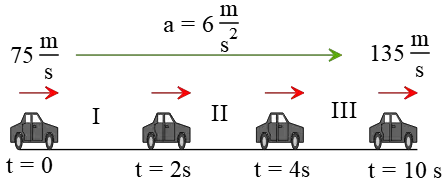
Because the problem tells us that the object accelerates uniformly, we can infer that its acceleration is constant throughout its entire path.
Given the initial and final velocities of the moving object, we can determine its acceleration using the definition of instantaneous acceleration as follows: \[a=\frac{v_2-v_1}{t_2-t_1}=\frac{135-75}{10}=6\,{\rm m/s^2}\] To analyze the motion between the requested times (referred to as stage II in the figure), we need some information for that time interval, such as their velocities or the distance between them.
As you can see in the figure, the initial velocity of stage II is the final velocity of stage I. By using a relevant kinematics equation that relates these data to each other, we find that \begin{align*} v&=v_0+at\\\\&=75+(6)(2) \\\\&=87\,{\rm m/s}\end{align*} This velocity will be the initial velocity for stage II of the motion. Now, all the known information for stage II is as follows: initial velocity $v_0=87\,{\rm m/s}$, acceleration $a=6\,{\rm m/s^2}$, and time interval $\Delta t=2\,{\rm s}$. The unknown is the distance traveled, denoted by $x=?$
The appropriate equation that relates all these variables is $x=\frac 12 at^2+v_0t+x_0$. Substituting the known values, we get \begin{align*}x&=\frac 12 at^2+v_0t+x_0\\\\&=\frac 12 (6)(2)^2+(87)(2)+0\\\\&=186\quad {\rm m}\end{align*} Hence, our moving object travels a distance of 186 m between the instances of 2 s and 4 s.
Problem (11): A fast car starts from rest and accelerates at a uniform rate of $1.5\,{\rm m/s^2}$ for 4 seconds. After a while, the driver applies the brakes for 3 seconds, causing the car to uniformly slow down (decelerate) at a rate of $-2\,{\rm m/s^2}$.
(a) How fast is the car at the end of the braking period?
(b) How far has the car traveled after the braking period?
Solution: This motion is divided into two parts. First, draw a diagram and specify each section's known kinematics quantities.
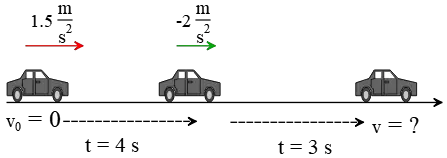
(a) In the first part, given the acceleration, initial velocity, and time interval, we can calculate the final velocity at the end of 4 seconds. \begin{align*} v&=v_0+at\\&=0+(1.5)(4) \\&=6\quad {\rm m/s}\end{align*} This velocity is considered as the initial velocity for the second part, where we want to find the final velocity.
In the next part, given the magnitude of acceleration and braking time interval, we can calculate the final velocity as follows: \begin{align*} v&=v_0+at\\&=6+(-2)(3) \\&=0\end{align*} The zero velocity here indicates that the car comes to a stop after the braking period.
(b) The distance traveled in the second part can now be calculated using the kinematics equation $x=\frac 12 at^2+v_0t+x_0$, because the only unknown quantity is distance $x$. \begin{align*} x&=\frac 12 at^2+v_0t+x_0\\\\&=\frac 12 (-2)(3)^2+(6)(3)+0\\\\&=+9\quad {\rm m}\end{align*} Therefore, after braking, the car travels a distance of 9 meters before coming to a stopped.
Problem (12): A car moves at a speed of 20 m/s down a straight path. Suddenly, the driver sees an obstacle in front of him and applies the brakes. Before the car reaches a stop, it experiences an acceleration of $-10\,{\rm m/s^2}$.
(a) After applying the brakes, how far did it travel before stopping?
(b) How long does it take the car to reach a stop?
Solution: As always, the first and most important step in solving a kinematics problem is to draw a diagram and input all known values into it, as shown below.
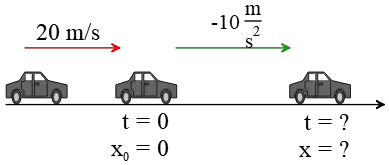
(a) The kinematics equation $v^2-v_0^2=2a(x-x_0)$ is the perfect equation to use here, as the only unknown quantity in it is the distance traveled, denoted by $x$. Thus, \begin{align*} v^2-v_0^2&=2a(x-x_0) \\\\ 0^2-(20)^2&=2(-10)(x-0) \\\\\Rightarrow \quad x&=\frac {-400}{-20}\\\\&=20\quad {\rm m}\end{align*}
(b) The phrase "How long does it take'' asks us to find the time interval. The initial and final velocities, as well as acceleration, are known, so the only relevant kinematics equation is $v=v_0+at$. Thus, \begin{align*} v&=v_0+at\\\\0&=20+(-10)t\\\\\Rightarrow t&=\frac{-20}{-10}\\\\&=2\quad {\rm s}\end{align*} Therefore, after braking, the car moves for 2 seconds before coming to a stop.
Problem (13): A sports car moves a distance of 100 m in 5 seconds with a uniform speed. Then, the driver brakes, and the car, comes to a stop after 4 seconds. Find the magnitude and direction of its acceleration (assumed constant).
Solution: uniform speed means constant speed or zero acceleration for the motion before braking. Thus, we can use the definition of average velocity to find its speed just before braking as below \begin{align*} \bar{v}&=\frac{\Delta x}{\Delta t}\\\\&=\frac{100}{5}\\\\&=20\quad {\rm m/s}\end{align*} Now, we know the initial and final velocities of the car in the braking stage. Since the acceleration is assumed to be constant, by applying the definition of average acceleration, we would have \begin{align*} \bar{a}&=\frac{v_2-v_1}{\Delta t}\\\\&=\frac{0-20}{4}\\\\&=-5\quad {\rm m/s^2}\end{align*} The negative shows the direction of the acceleration, which is toward the negative $x$-axis.
Hence, the car's acceleration has a magnitude of $5\,{\rm m/s^2}$ in the negative $x$ direction.
Problem (14): A race car accelerates from rest at a constant rate of $2\,{\rm m/s^2}$ in 15 seconds. It then travels at a constant speed for 20 seconds, and after that, it comes to a stop with an acceleration of $2\,{\rm m/s^2}$.
(a) What is the total distance traveled by car?
(b) What is its average velocity over the entire path?
Solution: To solve this kinematics question, we divided the entire path into three parts.
Part I: "From rest'' means the initial velocity is zero. Thus, given the acceleration and time interval, we can use the kinematics equation $v=v_0+at$ to calculate the distance traveled by the car at the end of 15 seconds for the first part of the path. \begin{align*} x&=\frac{1}{2}at^2 +v_0 t+x_0\\\\&=\frac 12 (2)(15)^2 +(0)(15)+0\\\\&=\boxed{125\quad{\rm m}}\end{align*}
As a side calculation, we find the final velocity for this part as below \begin{align*}v&=v_0+at\\\\&=0+(2) (15) \\\\&=30\quad {\rm m/s}\end{align*}
Part II: the speed in this part is the final speed in the first part because the car continues moving at this constant speed after that moment.
The constant speed means we are facing zero acceleration. As a result, it is preferable to use the average velocity definition rather than the kinematics equations for constant (uniform) acceleration.
The distance traveled for this part, which takes 20 seconds at a constant speed of 30 m/s, is computed by the definition of average velocity as below \begin{align*} \bar{v}&=\frac{\Delta x}{\Delta t}\\\\30&=\frac{\Delta x}{20}\end{align*} Thus, we find the distance traveled as $\boxed{x=600\,{\rm m}}$.
Part III: In this part, the car comes to a stop, $v=0$, so its acceleration must be a negative value as $a=-2\,{\rm m/s^2}$. Here, the final velocity is also zero. Its initial velocity is the same as in the previous part.
Consequently, the best kinematics equation that relates those known to the wanted distance traveled $x$, is $v^2-v_0^2=2a(x-x_0)$. \begin{align*} v^2-v_0^2&=2a(x-x_0) \\\\0^2-(30)^2&=2(-2)(x-0) \\\\ \Rightarrow \quad x&=\boxed{225\quad {\rm m}}\end{align*} The total distance traveled by car for the entire path is the sum of the above distances \[D=125+600+225=\boxed{950\quad {\rm m}}\]
Problem (15): A ball is dropped vertically downward from a tall building of 30-m-height with an initial speed of 8 m/s. After what time interval does the ball strike the ground? (take $g=-10\,{\rm m/s^2}$.)
Solution: This is a free-falling kinematics problem. As always, choose a coordinate system along with the motion and the origin as the starting point.
Here, the dropping point is considered the origin, so in all kinematics equations, we set $y_0=0$. By this choice, the striking point is 30 meters below the origin, so in equations, we also set $y=-30\,{\rm m}$.
Remember that velocity is a vector in physics whose magnitude is called speed. In this problem, the initial speed is 8 m/s downward. This means that the velocity vector is written as $v=-8\,{\rm m/s}$.
Now that all necessary quantities are ready, we can use the kinematics equation $y=\frac 12 at^2+v_0t+y_0$, to find the wanted time that the ball strikes the ground. \begin{align*} y&=\frac 12 at^2+v_0t+y_0\\\\-30&=\frac 12 (-10)t^2+(-8)t+0\end{align*} After rearranging, a quadratic equation like $5t^2+8t-30=0$ is obtained, whose solutions are given as below: \begin{gather*} t=\frac{-8\pm\sqrt{8^2-4(5)(-30)}}{2(5)}\\\\ \boxed{t_1=1.77\,{\rm s}} \quad , \quad t_2=-3.37\,{\rm s}\end{gather*} $t_1$ is the accepted time because the other is negative, which is not acceptable in kinematics. Therefore, the ball takes about 1.7 seconds to hit the ground.
Note: The solutions of a quadratic equation like $at^2+bt+c=0$, where $a,b,c$ are some constants, are found by the following formula: \[t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
Problem (16): The acceleration versus time graph for an object that moves at a constant speed of 30 m/s is shown in the figure below. Find the object's average velocity between instances $t_1=10\,{\rm s}$ and $t_2=30\,{\rm s}$.
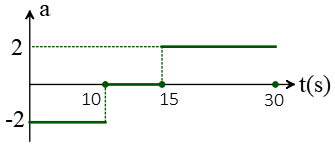
Solution: The best and shortest approach to solving such a kinematics problem is to first draw its velocity-vs-time graph. Next, the area under the obtained graph gives us the total displacement, which is divided by the total time interval to yield the average velocity.
The path consists of three parts with different accelerations.
In the first part, the object slows down its motion at a constant rate of $-2\,{\rm m/s^2}$ in 10 seconds. Its initial velocity is also 30 m/s. With these known quantities in hand, the kinematics equation $v=v_0+at$ gives us the velocity at the end of this time interval. \begin{align*} v&=v_0+at\\&=30+(-2)(10) \\&=10\quad {\rm m/s}\end{align*} This calculation corresponds to a straight line between the points $(v=30\,{\rm m/s},t=0)$ and $(v=10\,{\rm m/s},t=10\,{\rm s})$ on the $v-t$ graph as shown below.
Next, the object moves with zero acceleration for 5 seconds, which means the velocity does not change during this time interval. This implies that we must draw a horizontal line in the $v-t$ graph.
In the last part, the object accelerates from 10 m/s with a constant rate of $+2\,{\rm m/s^2}$ in 15 seconds. Thus, its final velocity at the end of this time interval is determined as below \begin{align*} v&=v_0+at\\&=10+(2)(15) \\&=40\quad {\rm m/s}\end{align*} Now, it's time to draw the velocity-vs-time graph. As an important point, note that all these motions have a constant acceleration, so all parts of a velocity-time graph, are composed of straight-line segments with different slopes.
For part I, we must draw a straight-line segment between the velocities of 30 m/s and 10 m/s.
Part II is a horizontal line since its velocities are constant during that time interval, and finally, in Part III, there is a straight line between velocities of 10 m/s and 40 m/s.
All these verbal phrases are illustrated in the following velocity-vs-time graph.
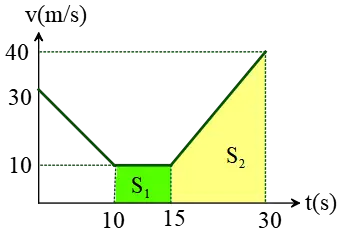
Recall that the area under a velocity vs. time graph always gives the displacement. Hence, the area under the $v-t$ graph between 10 s and 30 s gives the displacement. Therefore, the areas of rectangle $S_1$ and trapezoid $S_2$ are calculated as below \begin{gather*} S_1 =10\times 5=50\quad {\rm m} \\\\S_2=\frac{10+40}{2}\times 15=375\quad {\rm m}\end{gather*} Therefore, the total displacement in the time interval $[15,30]$ is \[D=S_{tot}=S_1+S_2=425\,{\rm m}\] From the definition of average velocity, we have \[\bar{v}=\frac{displacement}{time}=\frac{425}{20}=21.25\,{\rm m/s}\]
Challenging Kinematics Problems
In the following, some challenging kinematics problems are presented for homework.
A driver is moving along at $45\,\rm m/s$ when she suddenly notices a roadblock $100\,\rm m$ ahead. Can the driver stop the vehicle in time to avoid colliding with the obstruction if her reaction time is assumed to be $0.5\,\rm s$ and her car's maximum deceleration is $5\,\rm m/s^2$?
Solution: The time between seeing the obstacle and taking action, such as slamming on the brake, is defined as the reaction time. During this time interval, the moving object travels at a constant speed.
Thus, in all such questions, we have two phases. One is constant speed, and the other is accelerating with negative acceleration (deceleration).
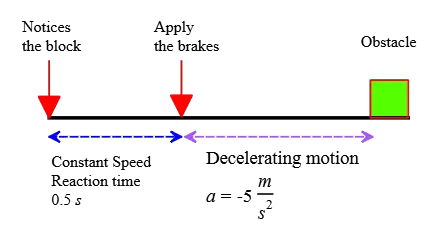
Here, between the time of seeing the barrier and the time of braking, the driver covers a distance of \begin{align*} x_1&=vt_{reac} \\\\ &=25\times 0.5 \\\\ &=12.5\,\rm m\end{align*} In the decelerating phase, the car moves a distance, which is obtained using the following kinematics equation: \begin{gather*} v^2-v_0^2=2ax_2 \\\\ (0)^2-(25)^2=2(-5) x_2 \\\\ \Rightarrow x_2=62.5\,\rm m\end{gather*} Summing these two distances gives a total distance that is a good indication of whether the moving object hits the obstacle or not. \begin{gather*} \Delta x_{actual}=x_1+x_2=75\,\rm m \\\\ \Rightarrow \Delta x_{covered}<\Delta x_{actual} \end{gather*} As a result, because the distance covered by the car is less than the actual distance between the time of seeing the barrier and the obstacle itself, the driver has sufficient time to stop the car in time to avoid a collision.
For a moving car at a constant speed of $90\,\rm km/h$ and a human reaction time of $0.3\,\rm s$; find the stopping distance if it slows down at a rate of $a=3\,\rm m/s^2$.
Solution: We use SI units, so first convert the given speed in these units as below \begin{align*} v&=90\,\rm km/h \\\\ &=\rm 90\times \left(\frac{1000\,m}{3600\,s}\right) \\\\ &=25\,\rm m/s\end{align*} As we said previously, during the reaction time, your car moves at a constant speed and covers a distance of \begin{align*} x_1&=vt_{react} \\\\ &=(25)(0.3) \\\\ &=7.5\,\rm m \end{align*} Deceleration means the moving object slows down, or a decrease per second in the velocity of the car occurs. In this case, we must put the acceleration with a negative sign in the kinematics equations.
During the second phase, your car has negative acceleration and wants to be stopped. Thus, the distance covered during this time interval is found as follows \begin{align*} v^2-v_0^2=2a\Delta x \\\\ (0)^2-(25)^2=2(3)\Delta x \\\\ \Rightarrow \quad \boxed{\Delta x=104.17\,\rm m}\end{align*}
Assume you are traveling $35\,\rm m/s$ when suddenly you see red light traffic $50\,\rm m$ ahead. If it takes you $0.456\,\rm s$ to apply the brakes and the maximum deceleration of the car is $4.5\,\rm m/s^2$,
(a) Will you be able to stop the car in time?
(b) How far from the time of seeing the red light will you be?
Solution: When you see the red light until you apply the brakes, your car is moving at a constant speed. This time interval is defined as the reaction time, $\Delta t_{react}=0.456\,\rm s$. After you get the brakes on, the car starts to decelerate at a constant rate, $a=-4.5\,\rm m/s^2$. Pay attention to the negative signs of such problems. The negative tells us that the car is decreasing its speed.
(a) In the first phase, the car moves a distance of \begin{align*} x_1&=v\Delta t_{react} \\\\ &=35\times 0.455 \\\\ &=15.96\,\rm m\end{align*} In the phase of deceleration, the car is moving a distance whose magnitude is found using the time-independent kinematics equation as below \begin{gather*} v^2-v_0^2=2ax_2 \\\\ (0)^2-(35)^2=2(4.5)x_2 \\\\ \Rightarrow \quad x_2=136.11\,\rm m\end{gather*} The sum of these two distances traveled gives us the total distance covered by the car from the time of seeing the red traffic light to the moment of a complete stop. \[x_{tot}=x_1+x_2=152.07\,\rm m \] Because the total distance traveled is greater than the actual distance to the red light, the driver will not be able to stop the car in time.
(b) As previously calculated, the total distance traveled by the car is nearly $152\,\rm m$ or the car is about $102\,\rm m$ past the red light traffic.
A person stands on the edge of a $60-\,\rm m$-high cliff and throws two stones vertically downward, $1$ second apart, and sees they both reach the water simultaneously. The first stone had an initial speed of $4\,\rm m/s$.
(a) How long after dropping the first stone does the second stone hit the water?
(b) How fast was the second stone released?
(c) What is the speed of each stone at the instant of hitting the water?
Solution: Because all quantities appearing in the kinematics equation are vectors, we must first choose a positive direction. Here, we take up as a positive $y$ direction.
Both stones arrived in the water at the same time. Thus, calculate the time the first stone was in the air. Next, use the time interval between the two drops to find the duration the second stone was in the air.
(a) The first stone is released downward at a speed of $4\,\rm m/s$, thus, its initial velocity is $v_0=-4\,\rm m/s$. The minus sign is for moving in the opposite direction of the chosen direction.
The only relevant kinematics equation that relates this known information is $\Delta y=-\frac 12 gt^2+v_0t$, where $\Delta y=-60\,\rm m$ is the vertical displacement, and the negative indicates that the stone hit a point below the chosen origin. Substituting the numerical values into this and solving for the time duration $t$ gives \begin{gather*} \Delta y=-\frac 12 gt^2+v_0t \\\\ -60=-\frac 12 (10)t^2+(-4)t \\\\ 5t^2+4t-60=0 \\\\ \Rightarrow \boxed{t=3.0\,\rm s} \, , \, t'=-3.8\,\rm s \end{gather*} The second answer is not acceptable.
(b) The second stone was released $1$ second after throwing the first one and arrived at the same time as the first stone. Therefore, the time interval that the second stone was in the air is found to be \begin{align*} t_2&=t_1-1 \\ &=3.0-1\\ &=2\,\rm s\end{align*}
(c) It is better to apply the time-independent kinematics equation $v^2-v_0^2=-2g\Delta y$ to find the stone's velocity at the moment it hit the water. For the first stone, we have \begin{gather*} v^2-v_0^2=-2g\Delta y \\\\ v^2-(-4)^2=-2(10)(-60) \\\\ \Rightarrow \quad \boxed{v=34.8\,\rm m/s} \end{gather*} The second stone's velocity is left to you as an exercise.
In a tennis game, the ball leaves the racket at a speed of $75\,\rm m/s$ whereas it is in contact with the racket for $25\,\rm ms$, and starts at rest. Assume the ball experiences constant acceleration.
(a) What was the ball's acceleration during this serve?
(b) How far has the ball traveled on this serve?
Solution: In this question, we are asked to find the ball's acceleration and distance traveled during that pretty small time interval.
(a) In a time interval of $\Delta t=25\times 10^{-3}\,\rm s$, we are given the beginning velocity $v_1=0$ and the end velocity $v_2=85\,\rm m/s$. Because it is assumed the acceleration is constant, the average acceleration definition, $a=\frac{\Delta v}{\Delta t}$, is best suited for these known quantities. \begin{align*} a&=\frac{v_2-v_1}{\Delta t} \\\\ &=\frac{75-0}{25\times 10^{-3}} \\\\ &=3000\,\rm m/s^2 \end{align*} A huge acceleration is given to the tennis ball.
(b) Here, we are asked to find the amount of distance traveled by the ball during the time the ball was in contact with the racket. Because we have a constant acceleration motion, it is best to use the following equation to find the distance traveled. \begin{align*} \Delta x&=\frac{v_1+v_2}{2}\times \Delta t \\\\ &=\frac{0+75}{2}\times (25\times 10^{-3}) \\\\ &=937.5\times 10^{-3}\,\rm m\end{align*} In millimeters, $\Delta x=937.5\,\rm mm$, and in centimeters $\Delta x=93.75\,\rm cm$. Therefore, during this incredibly short time interval, the ball moves about $94\,\rm cm$ along with the racket.
Starting from rest and ending at rest, a car travels a distance of $1500\,\rm m$ along the $x$-axis. During the first quarter of the distance, it accelerates at a rate of $+1.75\,\rm m/s^2$, while for the remaining distance, its acceleration is $-0.450\,\rm m/s^2$.
(a) What is the time travel of the whole path?
(b) What is the maximum speed of the car over this distance?
Solution: (a) This question consists of two parts. In the first part, the known values are $v_0=0$, $a=1.75\,\rm m/s^2$, $\Delta x=\frac 14 \times 1500=375\,\rm m$. The unknown is the time travel in this path, $t=?$, which is found using the following kinematics equation \begin{gather*} \Delta x=\frac 12 at^2+v_0 t\\\\ 375=\frac 12 (1.75)t^2+(0)t \\\\ t=\sqrt{\frac{2\times 375}{1.75}} \\\\ \Rightarrow t=20.70\,\rm s\end{gather*} For the second part of the path, the known values are $v_0=?$, $v_f=0$, $\Delta x=1500-375=1125\,\rm m$, $a=-0.450\,\rm m/s^2$. The unknown is the time taken in this part, $t'=?$.
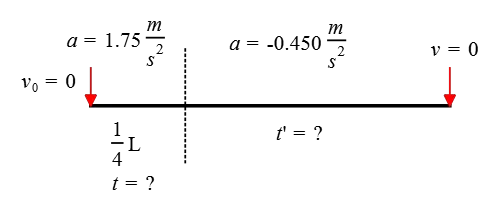
None of the time-dependent kinematics equations give us the time travel $t'$ without knowing the initial speed at the instant of the start of this second path.
We can find it using the equation $v^2-v_0^2=2a\Delta x$, setting $v=0$ at the end of the path, and solving for $v_0$ \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ (0)^2-v_0^2=2(-0.450)(1125) \\\\ v_0=\sqrt{2\times 0.45\times 1125} \\\\ \Rightarrow v_0=31.82\,\rm m/s\end{gather*} Given that, one can use the simple equation $v=v_0+at$ and solve for the time travel in this part of the path. \begin{gather*} v=v_0+at \\\\ 0=31.82+(-0.450)t' \\\\ \Rightarrow t'=70.71\,\rm s\end{gather*} Therefore, the total time traveled over the entire path is the sum of these two times. \begin{align*} T&=t+t' \\\\ &=20.70+70.71 \\\\ &=\boxed{91.41\,\rm s} \end{align*}
A train that is $75$ meters long starts accelerating uniformly from rest. When the front of the train reaches a railway worker who is standing $150$ meters away from where the train started, it is traveling at a speed of $20\,\rm m/s$. What will be the speed of the last car as it passes the worker?
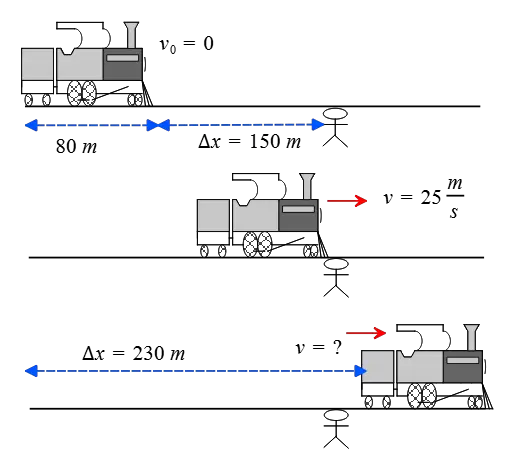
Solution: The front of the train is initially $150\,\rm m$ away from the worker, and when it passes him, it has a speed of $25\,\rm m/s$. From this data, we can find the acceleration of the front of the train (which is the same acceleration as the whole train) by applying the following kinematics equation \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ (25)^2-(0)^2=2a\times 150 \\\\ \Rightarrow \quad a=2.08\,\rm m/s^2\end{gather*} Given the train's acceleration, now focus on the last car.
The last car is initially at rest and placed at a distance of $150+80=230\,\rm m$ away from the person. When it passes the person, it has traveled $\Delta x= 230\,\rm m$ and its speed is determined simply as below \begin{gather*} v^2-v_0^2=2a\Delta x \\\\ v^2-(0)^2=2(2.08)(230) \\\\ \Rightarrow \quad \boxed{v=30.93\,\rm m/s}\end{gather*}
A wildcat moving with constant acceleration covers a distance of $100\,\rm m$ apart in $8\,\rm s$. Assuming that its speed at the second point is $20\,\rm m/s$,
(a) What was its speed in the first place?
(b) At what rate does its speed change over this distance?
Solution: First of all, list all known data given to us. Time interval $\Delta t=8\,\rm s$, the horizontal displacement $\Delta x=100\,\rm m$, speed at second point $v_2=20\,\rm m/s$.
We are asked to find the speed at the second point. To solve this kinematics problem, we use the following kinematics equation because the acceleration is constant and this is the most relevant equation that relates the known to the unknown quantities. \begin{gather*} \Delta x=\frac{v_1+v_2}{2}\times \Delta t \\\\ 100=\frac{v_1+20}{2}\times 8 \\\\ \Rightarrow \quad \boxed{v_1=5\,\rm m/s} \end{gather*} Therefore, the wildcat's speed in the first place is $5\,\rm m/s$.
In this part, we should find the wildcat's acceleration because acceleration is defined as the time rate of change of the speed of a moving object. Given the first place speed, $v_1=5\,\rm m/s$, found in the preceding part, we can use the following time-independent kinematics equation to find the wanted unknown. \begin{gather*} v_2^2-v_1^2=2a\Delta x \\\\ (20)^2-(5)^2=2a(100) \\\\ \Rightarrow \quad \boxed{a=1.875\,\rm m/s^2}\end{gather*}
Summary
In this tutorial, all concepts about kinematics equations are taught in a problem-solution strategy.
We can also find these kinematic variables using a position-time or velocity-time graph. Because slopes in those graphs represent velocity and acceleration, respectively, and the concavity of a curve in a position vs. time graph shows the sign of its acceleration in an x-t graph as well.
These multiple-choice questions on kinematics for AP Physics 1 are also available to review for students enrolled in AP Physics courses.
Author: Dr. Ali Nemati
Date published: 8-7-2021
Updated: June 12, 2023
© 2015 All rights reserved. by Physexams.com